SICP 105 - 元语言抽象
本文是对 Structure and Interpretation of Program - SICP 一书第四章“元数据抽象”的总结,包含了(几乎)所有习题的答案。元数据抽象提供给开发者看待和解决问题的新视角,在领域相关问题上可提供相比较通用程序设计语言更加简洁且具有表现力的解决方案。本文将介绍如何实现一个(不包含错误处理的基于 Scheme 基本过程和控制能力)的基本 Lisp 解释器,并且基于这种解释器的变形实现惰性求值、非确定性问题解决,并且在最后介绍了如何从头实现一门具有基本结构、组合能力和抽象能力的逻辑语言(数据查询语言)。
阿巴拉卡达巴拉 —— 在一个故事里的咒语在另一个中就不灵了,真正的魔力在于知道哪个咒语有用,在什么时候,用于做什么,其诀窍就在于学会有关的诀窍。就好比哈利波特:混血王子中斯内普发明的咒语,如果我们一直停留在学习和使用别人的咒语(程序语言和抽象表述方式)阶段,又怎么能够真正理解咒语本身呢?
软件工程就是克服设计复杂性的艺术,从基本元素组合成复合元素,从复合元素出发通过抽象形成更高层构建,并通过某种系统架构的观点保持系统的模块性。优秀的程序设计语言总是将试图解决复杂性问题作为最高目标,但随着面对特定领域问题的更加复杂,有时候不得不转向新的程序设计语言,通过新的原语、不同的组合方式、抽象方式来从不同的角度思考所面对的问题,以更有效的表述自己的想法 —— 这样的语言可以是专门为手头需要处理的问题打造的(这也是为什么我们不是用 TIOBE 排行榜上数百门更优秀的通用程序设计语言的原因,也是为什么程序设计语言一直在增多的原因)。比如电子网络语言基于电子元件(电阻、电容和晶体管)建模,电子系统语言基于信号处理模块(过滤器、放大器)建模,虽然系统语言基于网络语言的基础上构造起来的,但这种语言的分层能够直接的提供给我们更容易操作的原语和思维方式(以及对底层的完全的隔绝),就像之前的过程和数据抽象一样:比如实现一个轻松的正则序求值、进行非确定性计算、通过关系描述知识而非通过输入输出计算来描述。
而实现这一语言分层的方法就是通过“元语言抽象”,换言之,我们需要对某个程序设计语言设计求值器(解释器),用于执行求值这个表达式所要求的动作,求值器决定了一个程序设计语言中各个表达式的意义,而它本身不过是另一个程序。求值器其实并不少见,大到 javac, scalac, scheme repl, 小到多项式运算的算数规则和基于表结构的实现,之前的数字逻辑模拟器和约束传播系统,它们都有自己的基本操作、组合手段和抽象手段。换言之,计算机科学本身不过是关于如何构造适当的描述语言的学科,不论是过程抽象、数据抽象、模块化还是元语言抽象,其宗旨是一致的:构造基本操作、组合和抽象手段,使得开发者可以在一个更高的层次上认识和解决问题 —— 我们将看到,写一个元循环求值器的过程,并不是描述语言的基本过程,而是在有应用基本过程的能力的基础上,提供一套连接方式,组合手段和抽象手段,借助它们将基本过程联系起来,形成一个语言(比如处理组合嵌套、追踪和维护变量轨迹以允许使用变量、维护过程定义轨迹以允许复合过程定义、提供特殊形式进行特殊方式求值)。
元循环求值器
用与被求值的语言同样的语言写就的求值器称之为元循环。根据求值的环境模型,其核心包含两个部分:①对组合式每个子表达式求值,然后替换。②在复合过程中应用实际参数,通过创建新框架来扩充环境,将形参应用于实参约束。这两个过程是彼此依赖的,前者从环境绑定表达式实际参数(环境拉),后者产生新环境和新表达式(环境推)。
求值器的内核
求值的过程本质上就是 eval 和 apply 互相作用的过程,对于 eval 而言【环境拉】,其根据一个环境和表达式,对此表达式进行按照语法类型进行分类应用实际参数的处理。比如对于①基本表达式:自表达式 - 数直接返回此表达式本身,变量则在环境中进行查找,对于②特殊表达式,加引号则直接返回、赋值则递归调用新值并修改环境、if 表达式需要对各部分进行特殊处理,谓词为真返回推论部分,否则返回替代部分、lambda 转换为一个过程,然后将表达式参数表和求值环境包装起来、begin 按顺序求值表达式、cond 转换为嵌套 if 表达式然后求值,对于③组合式,则递归的求值运算符和运算对象,然后将得到的过程送给 apply 处理实际的过程应用。对于 apply 而言【环境推】,基本过程则直接处理,复合过程则先顺序求值组成过程体的表达式,与此同时建立相应的环境,加入一个框架,将过程中各个形式参数约束于过程调用的实际参数。

这是 eval 的核心代码,本质就是对语法的分情况讨论,自求值返回自身,变量则从环境查找绑定替换,引号直接返回,赋值先求值再更新环境中对应名称的值,定义先求值并将名称和值写入环境,if 执行谓语得到分支并求值此分支,lambda 则创建过程,begin 顺序求值,cond 转换为 if 处理(派生表达式),application 分别对运算符和运算对象分别处理然后 apply。

这是 apply 的核心代码,对于基础过程直接应用,对于复杂过程执行过程体,并且创建新环境将实参应用于形参以继续替换表达式进行规约。
表达式的表示(eval)
下面是 eval 的一个完全表示,list-of-values 用于顺序 eval 表达式,因为基于 Scheme 的解释器实现依赖底层 Scheme 实现语言表达式的求值顺序,因此这里进行了探测处理。eval-if 根据 if 数据抽象:if?, if-predicate 和 if-consequent, if-alternative, make-if 分别进行 eval 以实现谓词选择的语义。eval-sequence 用于顺序进行序列的 eval 求值,eval-definition, eval-assignment 通过和环境的交互实现了赋值和定义,eval-cond 实现了对于 cond 的直接处理,类似 eval-if,不过更为复杂,这里包含了 else 语句以及特殊 cond form:(cond ((assoc 'b '((a 1) (b 2))) => cadr)) 如果谓词后跟着 => 那么在谓词求值为真后,需要将其作为参数应用于 cadr 过程,得到的值作为 cond 返回的值,注意 cond 的谓词后动作可能为多个,因此这里使用 eval-sequence 处理而非 eval 处理。
(define (eval exp env)
(cond ((self-evaluating? exp) exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp) (make-procedure (lambda-parameters exp)
(lambda-body exp) env))
((let? exp) (eval (let->combination exp) env))
((let*? exp) (eval (let*->nested-lets exp) env))
((letrec? exp) (eval (letrec->let exp) env))
((begin? exp) (eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((callable? exp) (apply (eval (operator (cdr exp)) env)
(list-of-values (operands (cdr exp) env))))
((while? exp) (eval (while->lambda exp) env))
((not (eq? (get-hash-table actions (operator exp) 'NDF) 'NDF))
(apply-in-underlying-scheme
(get-hash-table actions (operator exp) 'NDF) env (operands exp)))
((application? exp)
(apply (eval (operator exp) env)
(list-of-values (operands exp) env)))
(else (error "Not defined to handle exp -- EVAL" exp))))
;;;;;;;;;; ACTION ;;;;;;;;;;;
(define (list-of-values exps env)
(define (is-left-to-right)
(define (order-detected)
(let ((init 0)) (lambda (new-value)
(if (= init 0) (begin (set! init 1) init) new-value))))
(let ((o (order-detected))) (= (+ (o 0) (o 1)) 2)))
(define (loop exps)
(if (no-operands? exps) '()
(cons (eval (first-operand exps) env)
(loop (rest-operands exps)))))
(define (reverse-loop items)
(cond ((null? items) '())
((null? (cdr items)) (car items))
(else (cons (reverse-loop items) (car items)))))
(if (is-left-to-right) (loop exps) (reverse-loop (loop exps))))
(define (eval-if exp env)
(if (true? (eval (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))
(define (eval-sequence exps env)
(cond ((last-exp? exps) (eval (first-exp exps) env))
(else (eval (first-exp exps) env)
(eval-sequence (rest-exps exps) env))))
(define (eval-assignment exp env)
(set-variable-value! (assignment-variable exp)
(eval (assignment-value exp) env) env) 'ok)
(define (eval-definition exp env)
(define-variable! (definition-variable exp)
(eval (definition-value exp) env) env) 'ok)
(define (eval-cond exp env)
;这里的 eval-cond 实现不健全,仅作为支持特殊 cond 形式支持的示意,实际应使用 cond->if
(define (eval-clauses clauses)
(if (null? clauses) '#f
(let ((first (car clauses)))
(cond ((cond-else-clause? first)
(eval-sequence (cond-actions first) env))
((cond-spec-form? first)
(let ((evaluted (eval (cond-predicate first) env)))
(if (true? evaluted)
(apply (eval (cond-spec-form-actions first) env)
(list evaluated)) '#f)))
(else (if (true? (eval (cond-predicate first) env))
(eval-sequence (cond-actions first) env))))
(eval-clauses (cdr clauses)))))
(eval-clauses (cond-clauses exp)))
可以看到 eval 本质上就是通过和环境的交互实现实际参数的绑定、赋值、定义,将表达式递归 eval 化归为基本形式的过程。为了实现这样的化归,我们需要根据语法来将其进行分别解析以分情况执行 eval-xxx。这就需要实现谓词,这里的谓词一般都很简单,self-evaluating? 判断是否为基础值,variable? 判断是否为符号,quoted? 判断是否为 quote 开头,为了简化这种根据表达式 car 符号判断特殊形式的调用,定义了 tagged-list? 过程,并且基于此实现了 assignment? 赋值判断,definition? 定义判断,lambda? 匿名表达式判断,if? 判断,begin? 判断,application? 判断,cond? 判断,let? 判断,let*? 判断,callable? 判断。为了让这些表达式类型和底层的序对/序列表示松耦合,这里除了谓词,一般还定义了选择函数和构造函数,比如 if 选择谓词、判断和替代分支的 if-predicate 和 if-consequent, if-alternative, make-if,这看起来比直接 car, cadr, caddr, cddr 要繁琐,但可以和底层实现隔离开的数据抽象能力方便我们对程序进行移植,避免和一种特定语法绑定,难以扩展,以实现比如 (1 2 3 +) 这样的语法形式。此外,为了避免之后增加表达式/扩充语法导致修改 eval,一般还会采用数据导向方式允许对 eval 进行扩充,这里使用了一张 hashtable 对基于这里匹配不到的 car 表达式字符进行分派的方法,并基于此实现了 and 和 or 的 eval 支持。
(define actions (make-hash-table))
(define (eval-and args env)
(if (null? args) #t
(if (eval (car args) env) (eval-and (cdr args) env) #f)))
(define (eval-or args env)
(if (null? args) #f
(if (eval (car args) env) #t (eval-or (cdr args) env))))
(define (eval-and-2 args env) ;;(if (a) (if (b) #t #f) #f)
(if (null? args) '#t
(make-if (car args) (eval-and-2 (cdr args)) '#f)))
(define (eval-or-2 args env) ;;(if (a) #t (if (b) #t #f))
(if (null? args) '#f
(make-if (car args) '#t (eval-or (cdr args)))))
(put-hash-table! actions 'and (lambda (env . args) (eval-and args env)))
(put-hash-table! actions 'or (lambda (env . args) (eval-or args env)))
最后,这里对于派生表达式,比如 let*, let, cond(不包含特殊形式), and, or, while 都提供了派生的表达,即先转换为基本表达式语法,然后再对这些基本表达式语法进行求值。这里的 cond->if 就是一个例子(但为了支持特殊形式的 cond,这里最终还是采用直接 eval-cond 以进行实现,如果采用 cond->if 形式,特殊形式 cond 谓词要被求值两次,这可能导致副作用),let->lambda 也是一个例子,这里为了支持特殊形式的命名 let,还实现了 let->comp-lambda,其本质就是构造一个 lambda 闭包,然后在其中构造一个 define 过程定义,再立刻调用这个过程,通过这种形式以允许在过程定义中使用 (fun-name x x) 这样的表达式。let*-> nested-lets 实现了 let 表达式顺序赋值的能力,本质就是转换为嵌套的 let 表达式。while->lambda 也是如此,这里生成了一个 lambda 闭包,里面内含一个特殊的过程,此过程末尾被插入如果谓词为真,则递归调用此过程,反之直接返回这个语句实现了 while 循环,然后立刻调用此过程。派生表达式是一种强大的技术,其允许我们复用现有表达式处理过程,基于此更简单的扩充和实现特殊形式语法 —— 在实际的 Lisp 中,这被称之为宏,即生成代码的代码。
;;;;;;;;;;;;;; PREDICATE ;;;;;;;;;;;;
(define (self-evaluating? exp) ;2, "Hello World"
(cond ((number? exp) #t) ((string? exp) #t) (else #f)))
(define (variable? exp) (symbol? exp))
(define (quoted? exp) (tagged-list? exp 'quote)) ;(quote xxx)
(define (text-of-quotation exp) (cadr exp))
(define (tagged-list? exp tag) (if (pair? exp) (eq? (car exp) tag) #f))
(define (assignment? exp) (tagged-list? exp 'set!)) ;(set! a 233)
(define (assignment-variable exp) (cadr exp)) ;a
(define (assignment-value exp) (caddr exp)) ;233
(define (definition? exp) (tagged-list? exp 'define))
;(define <var> <value>) or (define (<var> <pa>) <body>)
;(define <var> (lambda (<pa>) <body>)) same as the first condition
(define (definition-variable exp) ;<var>
(printf "[define-var] called\n")
(if (symbol? (cadr exp)) (cadr exp) (caadr exp)))
(define (definition-value exp)
(if (symbol? (cadr exp)) (caddr exp) ;<value>
(make-lambda (cdadr exp) (cddr exp)))) ;<pa>.. <body>..
(define (lambda? exp) (tagged-list? exp 'lambda)) ;(lambda (x y) a b)
(define (lambda-parameters exp) (cadr exp)) ;x y
(define (lambda-body exp) (cddr exp)) ;a b
(define (make-lambda parameters body) (cons 'lambda (cons parameters body)))
(define (if? exp) (tagged-list? exp 'if)) ;(if (<pre>) <a> <b> )
(define (if-predicate exp) (cadr exp))
(define (if-consequent exp) (caddr exp))
(define (if-alternative exp) (if (not (null? (cdddr exp))) (cadddr exp) '#f))
(define (make-if pre conse alt) (list 'if pre conse alt))
(define (begin? exp) (tagged-list? exp 'begin)) ;(begin (xxx) (yyy))
(define (begin-actions exp) (cdr exp))
(define (last-exp? seq) (null? (cdr seq)))
(define (first-exp seq) (car seq))
(define (rest-exps seq) (cdr seq))
(define (make-begin seq) (cons 'begin seq))
(define (sequence->exp seq) ;sequence to exp, sometime (begin xxx)
(cond ((null? seq) seq)
((last-exp? seq) (first-exp seq))
(else (make-begin seq))))
(define (application? exp) (pair? exp)) ;(operator operands...)
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))
(define (no-operands? ops) (null? ops))
(define (first-operand ops) (car ops))
(define (rest-operands ops) (cdr ops))
(define (cond? exp) (tagged-list? exp 'cond)) ;(cond (???))
(define (cond-clauses exp) (cdr exp)) ;(pred action..): (a b) or (else g)
(define (cond-else-clause? clause) (eq? (cond-predicate clause) 'else))
(define (cond-predicate clause) (car clause))
(define (cond-actions clause) (cdr clause))
(define (cond-spec-form? clause) (eq? (cadr clause) '=>)) ;(<pre> => <act>)
(define (cond-spec-form-actions clause) (caddr clause)) ;<act>
(define (cond->if exp)
(define (expand-clauses clauses)
(if (null? clauses) '#f
(let ((first (car clauses)) (rest (cdr clauses)))
(if (cond-else-clause? first)
(if (null? rest)
(sequence->exp (cond-actions first))
(error "else clause isn't last -- COND->IF" clauses))
(make-if (cond-predicate first)
(sequence->exp (cond-actions first))
(expand-clauses rest))))))
(expand-clauses (cond-clauses exp)))
(define (let? exp) (tagged-list? exp 'let))
;(let ((a 2) (b 3)) x y) -> ((lambda (a b) x y) 2 3)
(define (let->lambda exp)
(let ((var-pairs (cadr exp)) (body-exps (cddr exp)))
(cons (make-lambda (map car var-pairs) body-exps)
(map cadr var-pairs))))
;(let name ((a 2) (b 3)) x y (name a b)) ->
;((lambda () (define (name a b) x y (name a b)) (name 2 3)))
(define (make-define-lambda name vars body calls)
(list (list 'lambda '()
(cons 'define (cons (cons name vars) body))
(cons name calls))))
(define (let->comp-lambda exp)
(let ((name (cadr exp))
(var-smb (map car (caddr exp)))
(var-exp (map cadr (caddr exp)))
(body (cdddr exp)))
(make-define-lambda name var-smb body var-exp)))
(define (let->combination exp)
(if (and (symbol? (cadr exp)) (pair? (caddr exp)))
(let->comp-lambda exp) (let->lambda exp)))
;(let* ((x 3) (y (+ x 2)) (z (+ x y 5))) (* x z))
;(let ((x 3)) (let ((y (+ x 2))) (let ((z (+ x y 5))) (* x z))))
(define (let*? exp) (tagged-list? exp 'let*))
(define (let*->nested-lets exp)
(define (make-let var-pairs body-exp)
(list 'let var-pairs body-exp))
(define (nested-lets var-pairs body-seq)
(if (null? var-pairs) (sequence->exp body-seq)
(make-let (list (car var-pairs))
(nested-lets (cdr var-pairs) body-seq))))
(nested-lets (cadr exp) (cddr exp)))
(define (letrec? exp) (tagged-list? exp 'letrec))
(define (letrec-inits exp) (cadr exp))
(define (letrec-body exp) (cddr exp))
(define (letrec->let exp)
(cons 'let (cons (map (lambda (pair) (list (car pair) '*unassigned*))
(letrec-inits exp))
(append (map (lambda (pair)
(list 'set!
(car pair)
(cadr pair)))
(letrec-inits exp))
(letrec-body exp)))))
(define (callable? exp) (tagged-list? exp 'call)) ;(call + 1 2)
(define (while? exp) (tagged-list? exp 'while))
(define (while->lambda exp)
(let ((pre (cadr exp)) (body (cddr exp)))
(let ((new-body (append body (list (make-if pre (list 'fun) #t)))))
(make-define-lambda 'fun '() new-body '()))))
求值器数据结构(eval)
现在我们有了 eval 的谓词判断,可以处理多种语法形式,将派生表达式转换为表达式,对基本表达式进行 eval 划归求值,这些 eval 化归后的环境变量查找、更新和赋值的 API —— lookup-variable-value、set-variable-value! 和 define-variable! 需要基于环境和框架来处理,因此这里需要实现环境和框架的数据抽象:对于过程而言,其数据结构就是简单的加标签参数、过程体和环境序列。对于
环境而言,通过序对进行表示,序对 car 为框架,cdr 为关联上一个环境。对于框架而言,其保存了多个 variable-name 和 variable-value 对,这里通过序对来实现,其结构很巧妙,可以很方便的插入、更新数据:查找、更新和赋值变量都基于 env-loop 实现,简而言之,如果从一个环境找不到目标变量,则去其父环境寻找,直到找到为止,然后返回值、更新值或插入新值。
;;;;;;;;;;;;;;;;;; DATA STRUCTURE ;;;;;;;;;;;;;;;;;;;;
(define (true? x) (not (eq? x #f)))
(define (false? x) (eq? x #f))
;过程:复合过程本质就是参数、体和环境的序列
(define (make-procedure parameters body env)
(printf "[make-procedure] called!\n")
(list 'procedure parameters (scan-out-defines body) env))
注意,构建过程的时候有一些细微的问题需要处理,比如下图所示的内部定义,这里解释器能够正确运行的原因是一种偶然,因为 even? 定义调用的 odd? 在定义时(绑定到环境)并没有触发,odd? 也是的。但为了正确实现内部过程,我们一般需要将内部过程的名称(过程名)在过程体头部先绑定为空,然后再进行赋值,scan-out-defines 实现了这一过程,但是引入的 let 增加了环境框架,另一种方式是 scan-out-defines-faster,其直接在过程体头部为这些名称进行了绑定。

注意上图右侧这样的实现并不可取,比如对于 solve 而言,当定义 y 时,其过程将先被求值,这里 ok,但定义 dy 时,stream-map 会获取流的第一项,这时 y 还是 unassigned,就导致了错误。
最后再来看一种微妙的错误,下图所示的结果是不确定的,MIT 直接返回错误,因为 b 求值时的 a 在其框架被分配了 unassigned,以至于其不能找到上层环境的 1,因此报错。可以通过对过程体 define 非 lambda 进行重排序的方式实现依赖处理,让 a 先定义,依赖 a 的 b 后定义以解决问题。

实际上我们可以通过 letrec 允许在约束中递归,参见 eval 中 letrec 的处理,其本质就是 let unassigned 后在过程体最前面 set! 值,这样就允许了在 let 约束中进行递归(符号能找到)。
(define (scan-out-defines body) ;inside define level-up
(let* ((inside-defines (filter definition? body))
(other-bodys
(filter (lambda (e) (not (definition? e))) body))
(defines-names
(map (lambda (d)
(list (definition-variable d) '*unassigned*))
inside-defines))
(defines-2-set
(map (lambda (d)
(list 'set! (definition-variable d)
(definition-value d)))
inside-defines)))
(cons 'let (cons defines-names
(append defines-2-set other-bodys)))))
(define (scan-out-defines-faster body)
(let* ((inside-defines (filter definition? body))
(defines-unassigned
(map (lambda (d) (list 'define
(definition-variable d)
' *unassigned*))
inside-defines)))
(append defines-unassigned body)))
(define (compound-procedure? p) (tagged-list? p 'procedure))
(define (procedure-parameters p) (cadr p))
(define (procedure-body p) (caddr p))
(define (procedure-environment p) (cadddr p))
;环境:外围环境、环境的首个框架、空环境
(define (enclosing-environment env) (cdr env))
(define (first-frame env) (car env))
(define the-empty-environment '())
;框架:((k1 k2 k3) v1 v2 v3)
(define (make-frame variables values) (cons variables values))
(define (frame-variables frame) (car frame))
(define (frame-values frame) (cdr frame))
(define (add-binding-to-frame! var val frame)
(printf "[var-append!] add var to frame\n")
(set-car! frame (cons var (car frame)))
(set-cdr! frame (cons val (cdr frame))))
;(printf "[var-append!] now frame is ~a\n" frame))
(define (extend-environment vars vals base-env)
(if (= (length vars) (length vals))
(cons (make-frame vars vals) base-env)
(if (< (length vars) (length vals))
(error "Too many arguments supplied" vars vals)
(error "Too few arguments supplied" vars vals))))
注意,如果这里的框架实现为表的序对,那么查找将很简单,但是更新就比较麻烦,因为每次仅返回一个序对,无法就地更改原来的框架(必须在处理过程中包含上一个 key-value 序对,如果目标序对需要修改,那么将上一个序对 set-cdr! 即可,不过这种情况还要额外处理如果没有上一个序对的情况 —— 即目标序对为第一个,参见下文 make-unbound!-2),因此这里使用了一种讨巧的方法,让 car frame 为一个 label,这样就总是可以 set-cdr! frame 来改变序列值了。
(define (make-frame var val) (cons 'frame (map cons var val)))
(define (add-binding-to-frame! var val frame)
(set-cdr! frame (cons (cons var val) (cdr frame))))
(define (set-var-to-frame! var val frame)
(let ((find #f))
(set-cdr! frame
(map (lambda (pair)
(if (eq? (car pair) var)
(begin (set! find #t) (cons var val))
pair))
(cdr frame)))
find))
(define (set-variable-value! var val env)
(define (env-loop env)
(if (eq? env the-empty-environment)
(error "Unbound variable -- SET!" var)
(if (set-var-to-frame! (first-frame frame)) 'done
(env-loop (enclosing-environment env)))))
(env-loop env))
(define (define-variable! var val env)
(let ((frame (first-frame env)))
(if (set-var-to-frame! var val frame) 'done
(add-binding-to-frame! var val frame))))
当然,这里我们还是采用前者的实现,即框架作为 var 和 vals 的序对。下面提供了基于 env-loop 的在单个或多个框架中查找、赋值和定义的方法:本质就是对框架数据结构的修改。
;基于这些数据抽象可以实现变量查找、赋值和定义 API
(define (env-loop env var next match)
(define (scan vars vals)
(cond ((null? vars) (next env var next match))
((eq? var (car vars)) (match vars vals))
(else (scan (cdr vars) (cdr vals)))))
(if (eq? env the-empty-environment)
(error "Unbound variable" var)
(let ((frame (first-frame env)))
;(printf "[find-var?] in frame:~a\n" frame)
(scan (frame-variables frame)
(frame-values frame)))))
(define (lookup-variable-value var env)
(env-loop env var
(lambda (env var next match)
(env-loop (enclosing-environment env)
var next match))
(lambda (vars vals)
(let ((target (car vals)))
(printf "[find-var!]\n")
(if (eq? target '*unassigned*)
(error "lookup unassigned value!" 233)
target)))))
(define (set-variable-value! var val env)
(env-loop env var
(lambda (env var next match)
(env-loop (enclosing-environment env)
var next match))
(lambda (vars vals) (set-car! vals val))))
(define (define-variable! var val env)
(printf "[define-set!]\n")
(let ((frame (first-frame env)))
(env-loop env var
(lambda (env var next match)
(add-binding-to-frame! var val (first-frame env)))
(lambda (vars vals) (set-car! vals val)))))
最后,我们可能还想删除定义的变量,这里仅只是删除当前框架的(父框架删除没必要还容易影响依赖父环境的其他过程)。这里使用了两种方法,第一种更短,但效率更低,其基于 map、filter 实现删除,第二种稍长,但效率较高,其缺点是需要额外处理目标为 frame 首个元素的情况,如果目标不是首个元素,那么 scan 中通过操纵上一个元素的 set-cdr! 为当前元素下一个元素,即可实现删除。
(define (make-unbound! var env) ;4*linear
(let ((frame (first-frame env)))
(define pairs
(filter (lambda (pair) (not (eq? (car pair) var-target)))
(map cons (car frame) (cdr frame))))
(set-car! frame (map car pairs))
(set-cdr! frame (map cdr pairs))))
(define (make-unbound!-2 var env) ;linear
(let* ((frame (first-frame env))
(vars (frame-variables frame))
(vals (frame-values frame)))
(define (scan pre-vars pre-vals vars vals)
(if (not (null? vars))
(if (eq? var (car vars))
(begin (set-cdr! pre-vars (cdr vars))
(set-cdr! pre-vals (cdr vals)))
(scan vars vals (cdr vars) (cdr vals)))))
(if (not (null? vars))
(if (eq? var (car vars))
(begin (set-car! frame (cdr vars))
(set-cdr! frame (cdr vals)))
(scan vars vals (cdr vars) (cdr vals))))))
作为程序运行这个求值器(apply)
上述 eval 本质是在对环境中的表达式进行化归,不论是派生表达式还是特殊表达式,eval 的结束,就是 apply 的开始,不论是一个简单的 (+ 1 1) 还是 (eval '(+ 1 1)),其都需要 apply 进行处理:包括简单的调用 scheme 基本过程处理或者先派生新环境并替换形参以对过程体中的表达式交给 eval 进行表达式化归。
下面的过程用来创建了一个全局环境:setup-environment,环境本质就是 var 和 val 的绑定,因此这里做的事情就是为在全局环境中将一些基本过程名和 Scheme 对应过程名对应起来,然后为这些 Scheme 过程打上 'primitive 的标签,当遇到我们定义的过程名变量时,全局环境返回带有此 'primitive 标签的 Scheme 过程,在 apply-primitive-procedure 中将标签去掉,得到真实的 Scheme 过程并调用 Scheme 的 apply 进行执行。对于非基本过程,上述 make-procedure 会带上 'procedure 标签,因此我们的 apply 在这里判断非基本过程后,通过创建了新的派生环境,填充了形参变量名以及其实参值,然后通过 eval 执行过程体进行处理。
(define (setup-environment)
(let ((initial-env
(extend-environment (primitive-procedure-names)
(primitive-procedure-objects)
the-empty-environment)))
(define-variable! '#t #t initial-env)
(define-variable! '#f #f initial-env)
initial-env))
(define (primitive-implementation proc) (cadr proc))
(define primitive-procedures
(list (list 'car car) (list 'cdr cdr)
(list 'cons cons)
(list 'null? null?)
(list 'true #t) (list 'false #f)
(list 'square (lambda (x) (* x x)))
(list 'null '())
(list '+ +) (list '- -) (list '* *) (list '/ /)))
(define (primitive-procedure-names) ;true
(map car primitive-procedures))
(define (primitive-procedure-objects) ;('primitive #t)
(map (lambda (proc) (list 'primitive (cadr proc)))
primitive-procedures))
(define (primitive-procedure? proc)
(tagged-list? proc 'primitive))
(define (apply-primitive-procedure proc args)
;('primitive #t) -> (apply #t)
(apply-in-underlying-scheme
(primitive-implementation proc) args))
(define apply-in-underlying-scheme apply)
(define (apply procedure arguments)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure procedure arguments))
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters procedure) ;形参
arguments ;实参
(procedure-environment procedure)))) ;父环境
(else (error "Unknown procedure type -- APPLY" procedure))))
最后,我们通过 driver-loop 实现了一个 REPL 解释器前端,这里对输入的 Scheme 表达式通过 eval 函数进行求值,最后打印出来。
(define the-global-environment (setup-environment))
(define (driver-loop)
(display ">>")
(let ((input (read)))
(let ((output (eval input the-global-environment)))
(newline)
(user-print output)
(newline)))
(driver-loop))
(define (user-print object)
(if (compound-procedure? object)
(display (list 'compound-procedure
(procedure-parameters object)
(procedure-body object)
'<procedure-env>))
(display object)))
这个解释器最有意思的一点在于,它是一个完整的图灵机,而这台图灵机是建立在另一台图灵机(Chez Scheme 解释器)之上的,我们构建这台机器所做的唯一的事情就是将本节的代码作为数据输入给这个 Chez Scheme 解释器。这意味着任何有效的过程(可计算问题,参见丘奇-图灵论题)都可以描述为这台机器的一个程序,换言之,数据可以作为程序执行(Scheme 基本都带了一个叫做 eval 的过程,其可以接受作为数据的过程并返回对应结果)。考虑到这样一个相对简单的过程实现(我们实现的解释器)可以模拟许多比求值器本身还要复杂的各种程序,这看起来像是违反直觉 —— 但要知道,计算机本质上就是由只能计算加减的数字电路构成的,完全没有魔法可言,但我们的解释器通过层层抽象,以允许我们通过各种不同的形式(程序设计语言)来描述可计算问题,并逐层解释/编译执行以进行实现。可见过程和数据的界限本身就是模糊的,而这种模糊导致了“编程”看起来就像施魔法,我们送给机器一张写满符号的纸张的数据,机器就按照我们的要求执行对应的行为,发生在这背后的是数据通过解释器/编译器被一层层的解释为基本过程:加法、减法,然后通过数字电路进行了模拟并得到了结果。
将语法分析和执行分离
在上面 eval 计算的过程中,我们可以看到有很多冗余的重复语法分析,为了进一步提升速度,可以通过闭包机制实现预分析一次,之后直接分析后的表达式(因为有些表达式始终和环境相关,因此无法实际求值,只有等到具体环境中再进行计算)。analyze 类似于之前的 eval,对于自求值,返回闭包的自身,quoted 引号数据,返回去除引号的数据缓存,对于变量,其和环境相关,因此当传入 env 后再进行求值,对于赋值和定义而言,值可先化简,和符号一起缓存,等传入 env 后执行查询。对于 if 而言,断言、两个条件分支表达式都可以先化简。
(define (eval exp env)
((analyze exp) env))
(define (analyze exp)
(cond ((self-evaluating? exp)
(analyze-self-evaluating exp))
((quoted? exp) (analyze-quoted exp))
((variable? exp) (analyze-variable exp))
((assignment? exp) (analyze-assignment exp))
((definition? exp) (analyze-definition exp))
((if? exp) (analyze-if exp))
((let? exp) (analyze-let exp))
((lambda? exp) (analyze-lambda exp))
((begin? exp) (analyze-sequence (begin-actions exp)))
((cond? exp) (analyze (cond->if exp)))
((application? exp) (analyze-application exp))
(else (error "Unknown expression type -- ANALYZE" exp))))
(define (analyze-self-evaluating exp)
(lambda (env) exp))
(define (analyze-quoted exp)
(let ((qval (text-of-quotation exp)))
(lambda (env) qval)))
(define (analyze-variable exp)
(lambda (env) (lookup-variable-value exp env)))
(define (analyze-assignment exp)
(let ((var (assignment-variable exp))
(vproc (analyze (assignment-value exp))))
(lambda (env)
(set-variable-value! var (vproc env) env)
'ok)))
(define (analyze-definition exp)
(let ((var (definition-variable exp))
(vproc (analyze (definition-value exp))))
(lambda (env)
(define-variable! var (vproc env) env)
'ok)))
(define (analyze-if exp)
(let ((pproc (analyze (if-predicate exp)))
(cproc (analyze (if-consequent exp)))
(aproc (analyze (if-alternative exp))))
(lambda (env) (if (true? (pproc env))
(cproc env)
(aproc env)))))
对于 lambda 而言,要对 lambda 参数和体分别缓存,这里的体可能是一个序列,因此使用 analyze-sequence 进行缓存,这个过程实现的很有技巧,不仅对每个序列的表达式进行了分析,还将前后表达式绑定提供了上下文做了进一步的缓存分析。let 可先化归为 lambda 再套用 lambda 的分析过程。
(define (analyze-let exp)
(analyze-lambda (let->combination exp)))
(define (analyze-lambda exp)
(let ((vars (lambda-parameters exp))
(bproc (analyze-sequence (lambda-body exp))))
(lambda (env) (make-procedure vars bproc env))))
(define (analyze-sequence exp)
(define (sequentially proc1 proc2)
(lambda (env) (proc1 env) (proc2 env)))
(define (loop first-proc rest-procs)
(if (null? rest-procs) first-proc
(loop (sequentially first-proc (car rest-procs))
(cdr rest-procs))))
(let ((procs (map analyze exps)))
(if (null? procs)
(error "Empty sequence -- ANALYZE" 233))
(loop (car procs) (cdr procs))))
对于最终的过程应用而言,操作符、操作值都可以分析并缓存,具体的执行不再交给 apply,而是就地在 execute-application 中实现,对于复杂表达式,这里已经缓存过了,所以可直接对体应用扩展后的环境执行进一步的 eval。
(define (analyze-application exp)
(let ((fproc (analyze (operator exp)))
(aprocs (map analyze (operands exp))))
(lambda (env)
(execute-application (fproc env)
(map (lambda (aproc) (aproc env))
aprocs)))))
(define (execute-application proc args)
(cond ((primitive-procedure? proc)
(apply-primitive-procedure proc args))
((compound-procedure? proc)
((procedure-body proc)
(extend-environment (procedure-parameters proc)
args
(procedure-environment proc))))
(else (error "Unknown procedure type -- EXECUTE-APPLICATION" proc))))
这里的分析总体来看是有效的,虽然遇到变量、赋值、定义等还是会等到传入环境后才进行操作,但是这里的分析本质是用于缓存化简后的表达式,即规约掉中途的语法噪音,比如递归 factorial 过程,这里在递归的时候起码不会先 eval 分情况分析,找到 factorial 并确定它是一个 if 表达式,再对 if eval 分情况分析,求值谓词进行分派,而是可以直接将 factorial 和 if 缓存起来,当递归时直接进行一次查找 factorial 后直接缓存执行 if 谓词判断并继续执行化简后的分支表达式,提高了解释的效率。

惰性求值的实现
将某个参数尚未完成求值之前进入一个过程的体称之为过程相对于参数非严格,将某个参数进入过程体前完成求值称之为过程相对于参数严格。非严格和严格指的就是正则序和应用序,在一开始,我们就提到过这一问题,并且提到正则序的惰性求值可能将一个表达式求值多遍,因此一个通用性的解释器往往被设计为应用序求值,但是在流的章节,我们也看到了正则序还是存在用武之地的。

对于上图过程,应用序会导致无穷尽的计算(n = 1 时并不停止,因为始终要急计算参数 (* n (factorial (- n 1)),而正则序则可正常执行。
对于这里的 unless,我们可以使用特殊形式(宏、或者我们这里在自己解释器上将其实现为一种派生表达式)来实现,但是这种特殊形式将限制其和高阶过程结合工作,比如不能这样用:(define (choose left right) (unless left right 0)); (map choose '((#t 1) (#f 2) (#t 3) (#f 4)))。因此我们决定实现一个完全惰性的解释器:这里的原则是,对于 application? 谓词的判断,操作符直接求值,参数如果是复杂过程的话延迟求值,基本过程则直接返回值。这里的 apply 现在加入了 env 参数,对基本过程参数直接获取真实值并进行运算,对复杂过程参数进行延迟。当在 REPL 调用时,现在不能 eval 而必须 actual-value 调用以强制获取值。最后对于 eval-if 而言,谓词不能惰性必须立刻求值,除了这些,其余部分和正常解释器一样。
.. same as eval in normal interputer
((application? exp)
(apply (actual-value (operator exp) env)
(operands exp) env))
(define (apply procedure arguments env)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure procedure
(list-of-arg-values arguments env)))
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters procedure) ;形参
(list-of-delayed-args arguments env) ;实参
(procedure-environment procedure)))) ;父环境
(else (error "Unknown procedure type -- APPLY" procedure))))
(define (driver-loop)
(display ">>")
(let ((input (read)))
(let ((output (actual-value input the-global-environment)))
(newline)
(user-print output)
(newline)))
(driver-loop))
(define (eval-if exp env)
(if (true? (actual-value (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))
下面是一些辅助过程的实现,actual-value 从环境获取延迟后的表达式并执行强制求值(如果需要),比如 (+ 1 1),先找到 + 这个基本过程,这里不需要强制求值,因此 actual-value 返回 + 这个 primitive 数据结构,随后 1 和 1 传入,因为 + 是基本过程,所以 list-of-arg-values 用于对参数1 和 1 逐个强制求值得到结果。而如果是 (define (p x) x) (define a (p (p 10)) 这个过程,那么 p 首先被定义,(define a (p (p 10))) 调用时,(p (p 10)) 被 eval,这里 apply 不是基本过程,其运算符 p 被 actual-value 求值得到 lambda,创建新环境,返回参数本身,这里参数 (p 10) 被 list-of-delayed-args 惰性包装,这里惰性的实现方式:delay-it 是将参数和环境包装到一个数据结构中,前面打上 thunk 的标签,因此得到 ('trunk (p 10)),因此 a 现在为 'trunk (p 10),如果其要在 REPL 打印,那么通过 actual-value 的 force-it 可以简单的从数据结构取出数据 (p 10) 然后 eval,这里 eval 会对表达式求值,得到的结果为 10,结果不是一个惰性值,因此直接返回(如果是惰性值,那么递归继续 force-it 剥去标签在环境中继续求值表达式直到得到结果)。
(define (actual-value exp env) (force-it (eval exp env)))
(define (list-of-arg-values exps env)
(if (no-operands? exps) '()
(cons (actual-value (first-operand exps) env)
(list-of-arg-values (rest-operands exps) env))))
(define (list-of-delayed-args exps env)
(if (no-operands? exps) '()
(cons (delay-it (first-operand exps) env)
(list-of-delayed-args (rest-operands exps) env))))
; (define (force-it obj)
; (if (thunk? obj)
; (actual-value (thunk-exp obj) (thunk-env obj))
; obj))
(define (delay-it exp env) (list 'thunk exp env))
(define (thunk? obj) (tagged-list? obj 'thunk))
(define (thunk-exp thunk) (cadr thunk))
(define (thunk-env thunk) (caddr thunk))
为了提升效率,当进行一次 force-it 时(REPL 打印或者惰性值作为 if 谓词或作为操作符),在进行求值后将惰性值直接修改为已计算后的结果,当多次调用时直接返回结果,避免重复 eval 计算,提升效率,比如 (define (x3 x) (* x x x)),(define a (x3 (very-cost-procedure)))。
(define (evaluated-thunk? obj)
(tagged-list? obj 'evaluated-thunk))
(define (thunk-value evaluated-thunk) (cadr evaluated-thunk))
(define (force-it obj)
(cond ((thunk? obj)
(let ((result (actual-value (thunk-exp obj) (thunk-env obj))))
(set-car! obj 'evaluated-thunk)
(set-car! (cdr obj) result)
(set-cdr! (cdr obj) '())
result))
((evaluated-thunk? obj)
(thunk-value obj))
(else obj)))
下面是一个例子,其中 (define count 0) (define (id x) (set! count (+ count 1)) x)。这是 (define w (id (id 10))) 后的环境过程,当定义 id 后,定义 w 时,对 (id (id 10)) 进行 eval 进入 application? 分支,外面的 id 被 actual-value 得到 lambda 并求值,但是 x 被替换为 'thunk id 10 惰性存储,这时 count 为 1,当调用 w 被 REPL actual-value 时,对 'thunk id 10 进行 force it,进行 eval,同样的 count 变为 2,然后 w 被更新为计算后的结果,下次直接获取到 10,count 不会再增加。
+-------------------------------------------------------+
| count: 0 |(define count 0)
| id: (lambda (x) (set! ...)) <--> global environment |
global--+ |(define (id x)
| | (set! count (+ count 1))
| | x)
+-------------------------------------------------------+
+-------------------------------------------------------+
| count: 1 |
| id: (lambda (x) (set! ...)) <--> #global environment#|(define w (id (id 10)))
global--+ w: (thunk (id 10) #global environment#) | count
| |
| |
+-------------------------------------------------------+
+-------------------------------------------------------+
| count: 2 |
| id: (lambda (x) (set! ...)) <--> #global environment#|
global--+ w: (evaluated-thunk 10 #global environment#) |w
| |
| |
+-------------------------------------------------------+这里有几个有意思的小问题,eval 在 apply 时,能不能对操作符也懒加载而非直接计算 actual-value 呢?当然不可以,比如 (define (a b c) (b c)) (define (b c) (* c c)) (a b 2),如果操作符 a 惰性加载而非直接 force-it 得到 ‘thunk (b 2),而是 'thunk lambda、'thunk b 和 'thunk 2,那么当 force-it 的时候将直接对 'thunk b 求值,而非环境中的 b 过程,这导致出错。此外,考虑 begin 的求值方式,这里我们对每个表达式都惰性求值了,如果 force-it,那么将只强迫最后一个得到结果,在大部分情况下这样都工作很好,不过当存在副作用时,可能这种方式会导致结果因为惰性导致差异。

一种对 begin 的修改,对每个表达式均直接强迫求值而非惰性求值。对于 for-each 过程,这里 begin 的修改其实没有差别,因为 display 是基本程序会强迫 x 求值(apply 基本过程)。但是对这个副作用程序,如果 begin 均惰性求值,那么 (p1 1) 将得到 (1 . 2),而 (p2 1) 将得到 (1 .),因为这里的 e,即 set! 压根没有执行,如果 begin 均立即求值则结果为 (1 . 2)。
这个例子说明了惰性求值和副作用的天生“不搭”。最后,我们看到惰性求值是一种需求,但没必要将解释器完全实现为惰性的,可以基于基本解释器支持惰性行为,比如:(define (f a (b lazy) c (d lazy-memo)) 给提示让 b 惰性,d 惰性且记忆,这只需要在 apply 时处理参数时对形参标签判断并做出对应的行为,而处理形参时则需要去掉标记,如下所示(此部分代码依赖其他过程均为基础的解释器实现过程,没有语法分析或过程局部变量提升):
(define (apply procedure arguments env)
(cond ((primitive-procedure? procedure)
(apply-primitive-procedure
procedure
(list-of-arg-values arguments env)))
((compound-procedure? procedure)
(eval-sequence
(procedure-body procedure)
(extend-environment
(procedure-parameters-smb procedure) ;形参
(list-of-may-delayed-args
(procedure-parameters procedure)
arguments env) ;实参
(procedure-environment procedure)))) ;父环境
(else (error "Unknown procedure type -- APPLY" procedure))))
(define (eval exp env)
(cond ((self-evaluating? exp)
((variable? exp) (lookup-variable-value exp env))
((quoted? exp) (text-of-quotation exp))
((assignment? exp) (eval-assignment exp env))
((definition? exp) (eval-definition exp env))
((if? exp) (eval-if exp env))
((lambda? exp) (make-procedure
(lambda-parameters exp) (lambda-body exp) env))
((let? exp) (eval (let->combination exp) env))
((let*? exp) (eval (let*->nested-lets exp) env))
((letrec? exp) (eval (letrec->let exp) env))
((begin? exp) (eval-sequence (begin-actions exp) env))
((cond? exp) (eval (cond->if exp) env))
((callable? exp) (apply (eval (operator (cdr exp)) env)
(list-of-values (operands (cdr exp) env))))
((while? exp) (eval (while->lambda exp) env))
((not (eq? (get-hash-table actions (operator exp) 'NDF) 'NDF))
(apply-in-underlying-scheme
(get-hash-table actions (operator exp) 'NDF) env (operands exp)))
((application? exp)
(apply (actual-value (operator exp) env)
(operands exp) env))
(else (error "Not defined to handle exp -- EVAL" exp))))
(define (eval-if exp env)
(if (true? (actual-value (if-predicate exp) env))
(eval (if-consequent exp) env)
(eval (if-alternative exp) env)))
(define (driver-loop)
(display ">>")
(let ((input (read)))
(let ((output (actual-value input the-global-environment)))
(newline)
(user-print output)
(newline)))
(driver-loop))
其实这一版本的混合实现和惰性解释器版本更像,因为返回的表达式可能是懒加载的,因此所有需要 eval 的地方:eval-if 或者 driver-loop 都需要 actual-value 获取,如果其并非懒加载的,会直接获取到值。
如下是扩充的一些方法,对于懒加载现在通过标签区分是否要进行缓存,list-of-may-delayed-args 现在通过 params 来判断哪些表达式需要怎样加载并通过 delay-it 进行对应的行为,force-it 通过对标签判断以执行对应行为:执行并缓存、执行并不缓存、直接返回值,最后注意现在 apply complex procedure 时形参带有标签,因此要通过 procedure-parameters-smb 去除标签。
;(define f (lambda (a (b lazy) c (d lazy-memo)) ...))
;(f 1 (/ 2 0) 2 (/ 3 1))
(define (param-lazy? exp) (and (pair? exp) (eq? (cadr exp) 'lazy)))
(define (param-lazy-memo? exp) (and (pair? exp) (eq? (cadr exp) 'lazy-memo)))
(define (list-of-arg-values exps env)
(if (no-operands? exps) '()
(cons (actual-value (first-operand exps) env)
(list-of-arg-values (rest-operands exps) env))))
(define (list-of-may-delayed-args params exps env)
(if (no-operands? exps) '()
(let ((exp-now (first-operand exps))
(param-now (first-operand params)))
(cons (cond ((param-lazy? param-now) (delay-it #f exp-now env))
((param-lazy-memo? param-now) (delay-it #t exp-now env))
(else (actual-value exp-now env)))
(list-of-may-delayed-args
(rest-operands params)
(rest-operands exps) env)))))
(define (procedure-parameters-smb exps)
(map (lambda (exp) (if (pair? exp) (car exp) exp)) (cadr exps)))
(define (actual-value exp env) (force-it (eval exp env)))
(define (delay-it memo exp env) (list (if memo 'thunk-memo 'thunk) exp env))
(define (thunk-memo? obj) (tagged-list? obj 'thunk-memo))
(define (thunk-simple? obj) (tagged-list? obj 'thunk))
(define (thunk-exp thunk) (cadr thunk))
(define (thunk-env thunk) (caddr thunk))
(define (evaluated-thunk? obj) (tagged-list? obj 'evaluated-thunk))
(define (thunk-value evaluated-thunk) (cadr evaluated-thunk))
(define (force-it obj)
(cond ((thunk-memo? obj)
(let ((result (actual-value (thunk-exp obj) (thunk-env obj))))
(set-car! obj 'evaluated-thunk)
(set-car! (cdr obj) result)
(set-cdr! (cdr obj) '())
result))
((thunk-simple? obj)
(actual-value (thunk-exp obj) (thunk-env obj)))
((evaluated-thunk? obj) (thunk-value obj))
(else obj)))
(define (f a (b lazy) c (d lazy-demo)) (+ a c d))
(f 1 (/ 1 0) 3 4)
基于惰性求值器(并非这里实现的惰性和非惰性混合求值器)我们可以不使用流这种数据结构,而使用惰性的表(其更加惰性,不仅第二项懒加载,第一项也是懒加载的),在完全惰性求值器中可以执行如下定义和过程,注意这里的积分 integral 过程再也不用使用流,而是用惰性表即可构造,solve 也不用对 integral 进行特殊修改使得 integral 传入一个尚不存在的 dy 时被应用序 Scheme 解释器立刻求值(注意:要成功运行下面的过程,解释器不要使用 printf 或 display 进行打印,因为现在解释器是惰性的,打印的语句可能导致无穷循环)。
(define (cons x y) (lambda (m) (m x y)))
(define (car z) (z (lambda (p q) p)))
(define (cdr z) (z (lambda (p q) q)))
(define (list-ref items n)
(if (= n 0) (car items)
(list-ref (cdr items) (- n 1))))
(define (map proc items)
(if (null? items) '()
(cons (proc (car items)) (map proc (cdr items)))))
(define (scale-list items factor)
(map (lambda (x) (* x factor)) items))
(define (add-lists list1 list2)
(cond ((null? list1) list2)
((null? list2) list1)
(else (cons (+ (car list1) (car list2))
(add-lists (cdr list1) (cdr list2))))))
;(define ones (cons 1 ones))
;(define integers (cons 1 (add-lists ones integers)))
(define (integral integrand initial-value dt)
(define int
(cons initial-value (add-lists (scale-list integrand dt) int)))
int)
(define (solve f y0 dt)
(define y (integral dy y0 dt))
(define dy (map f y))
y)
(list-ref (solve (lambda (x) x) 1 .001) 1000)
这种惰性求值器的惰性表用途其实很广,不仅可以解决 stream 第二项数据经过过程参数传递时尚不存在但强制求值的问题,也可以避免第一项数据在非第一次实际调用时不想要的副作用问题,此外,第一项和第二项数据均惰性可让我们打造组合了无穷流的无穷矩阵,或者构造完全惰性 tree,tree 的分支是保存了过程的但尚未计算的数据。当然,这种惰性求值器的缺陷也很大,比如和赋值的强烈不兼容,以及对于 debug 的极端不友好,比如下面的 ones、inf-ones 定义时返回的过程都是 cons,没有任何其他信息。
(define show (cons (begin (display 'this-is-car) 'this-is-car) #t))
(define ones (cons 1 ones))
(define inf-ones (cons ones inf-ones))
(define (matrix-ref mat x y) (list-ref (list-ref mat x) y))
(matrix-ref inf-ones 5011 10)
注意,这个重写了 cons 的惰性表现在在执行 (car '(1 2 3)) 时会遇到错误,因为这里的引号在 eval 中的处理方式是使用内置的底层 Scheme cons 构建的,而非我们重定义的 cons,因此需要重新实现对于引号的处理 text-of-quotation,因为 list 本质是多个 cons,为了让这些 cons 都使用我们的定义,我们不得不为每个元素都使用 quote 括起来,让 eval 每次都通过我们的 cons 来构造 list。
(define (text-of-quotation exp env)
(let ((text (cadr exp)))
(if (pair? text) (eval (make-cons text) env) text)))
(define (make-cons exp)
(if (null? exp) (list 'quote '())
(list 'cons (list 'quote (first-operand exp))
(list 'quote (make-cons (rest-operands exp))))))
最后,惰性序对和表的打印看起来实在是太丑陋:指向 cons 定义过程。为了不对惰性 cons 求值同时美化打印,这里提供了一个简单的实现(很脆弱的实现,依赖于 cons 我们自己加载并且没有重写过):
(define (cons x y) (lambda (_cons_variable_) (_cons_variable_ x y)))
(define (user-print object)
(if (compound-procedure? object)
(if (and (not (null? (procedure-parameters object)))
(eq? (car (procedure-parameters object)) '_cons_variable_))
(display "cons(lazy,lazy) <procedure-env>")
(display (list 'compound-procedure
(procedure-parameters object)
(procedure-body object)
'<procedure-env>)))
(display object)))
非确定性求值
传统的计算机程序都是给定输入产生确定的输出,在一些场景下这样并不方便,比如“生成和检测”式的程序:需要使用深度优先算法求解的满足特定约束的问题(给定一些约束求解一个问题)、自然语言结构化解释的歧义性问题等。在这一节我们要实现一个非确定性求值的 Scheme 解释器,使用它的语法描述问题看上去就好像是单纯的在“描述问题”一样,而实际的深度优先算法则在解释器内部自动执行,这使得我们可以基于一个更高的抽象层次看问题。
我们要实现这个非确定性求值的解释器包含一个特殊形式:(amb <exp1> <exp2> ..),它返回传入的表达式之一。(require <pre>) 对一个条件进行判断,如果不满足则返回 (amb) 表示没有可用解。换言之,我们的解释器现在维护了一个深度优先结构,其包含一个可用值,require 进行谓词检测,如果不满足条件则调用 (amb),这个表达式在解释器中会告知一次执行失败和回滚以产生下一个可用值,直到满足或者没有可用结果为止。
(define (require p)
(if (not p) (amb)))
非确定性求值的例子
基于 amb 和 require 这两个 API,我们就可以发挥非确定性求值的威力,比如实现一个列表元素获取,an-element-of 获取列表元素,其返回的 amb 会试图获取 car 第一个元素,以及递归调用此方法获取下一个元素,当 items 为空,则 amb 返回的值会遇到 require 的 (amb) 而失败,这将在 REPL 打印一个没有可用解的提示并重新开始。an-integer-starting-from 用于获取 n 开始的元素,颇有点流的味道。prime-sum-pair 是使用 amb 求解两个列表元素和为素数的检测,这里如果深度递归树提供的 a 和 b 不足以 prime? 通过,则重新进入下一个分支,直到得到结果为止,比如 (3 20) (3 110),注意这里的执行通过 REPL 调用 try-again 命令来失败重试分支的,且这里的分支并不是两两配对,注意 a 一开始选择了 1,b 尝试了所有直到遇到 an-element-of 的 require 不满足条件(items 为空),然后失败回退 a 选择 3,b 选择 20 才满足 prime? 检测。
(define (an-element-of items)
(require (not (null? items)))
(amb (car items) (an-element-of (cdr items))))
(define (an-integer-starting-from n)
(amb n (an-integer-starting-from (+ n 1))))
(define (prime-sum-pair list1 list2)
(let ((a (an-element-of list1))
(b (an-element-of list2)))
(require (prime? (+ a b)))
(list a b)))
;(prime-sum-pair '(1 3 5 8) '(20 35 110))
下面是一个寻找毕达哥斯拉三元组的过程,即在给定界限内的 (I,j,k) 使得 I <= j 且 I * I + j * j = k * k,使用 amb 的方法很简单,利用 an-integer-between 过程生成范围数字,满足约束条件,调用 try-again 来走其他分支获取所有的解。
(define (a-pythagorean-triple-between low high)
(let* ((i (an-integer-between low high))
(j (an-integer-between i high))
(distance (an-integer-between j high)))
(require (= (+ (* i i) (* j j)) (* distance distance)))
(list i j distance)))
(define (an-integer-between low high)
(require (> high low))
(amb low (an-integer-between (+ low 1) high)))
毕达哥斯拉三元组另外的解法如下所示,a-py-truple-from 执行足够多 try-again 会获得所有可能的解,a-py-triple-between-2 则使用一种更优的策略提高了执行效率。
(define (a-pythagorean-triple-from low)
(let* ((i (an-integer-starting-from low))
(j (an-integer-between low i))
(distance (an-integer-between low j)))
(require (= (+ (* i i) (* j j)) (* distance distance)))
(list distance j i)))
(define (a-pythagorean-triple-between-2 low high)
(let ((i (an-integer-between low high))
(hsq (* high high)))
(let ((j (an-integer-between i high)))
(let ((ksq (+ (* i i) (* j j))))
(require (>= hsq ksq)))
(let ((distance (sqrt ksq)))
(require (integer? distance))
(list i j distance)))))
非确定性程序对于逻辑谜题非常适用,比如如下的问题可以简单创建一些约束然后返回满足约束的深度优先树的分支即可。

(define (distict? items)
(cond ((null? items) #t)
((null? (cdr items)) #t)
((member (car items) (cdr items)) #f)
(else (distict? (cdr items)))))
(define (member x items)
(cond ((null? items) #f)
((equal? x (car items)) #t)
(else (member x (cdr items)))))
(define (multiple-dwelling)
(let ((baker (amb 1 2 3 4 5))
(cooper (amb 1 2 3 4 5))
(fletcher (amb 1 2 3 4 5))
(miller (amb 1 2 3 4 5))
(smith (amb 1 2 3 4 5)))
(require (not (= backer 5)))
(require (not (= cooper 1)))
(require (not (= fletcher 5)))
(require (not (= fletcher 1)))
(require (> miller cooper))
(require (> (abs (- fletcher miller)) 1))
(require (not (= (abs (- smith fletcher)) 1)))
(require (not (= (abs (- fletcher cooper)) 1)))
(require (distict? (list baker cooper fletcher miller smith)))
(list (list 'baker baker)
(list 'cooper cooper)
(list 'fletcher fletcher)
(list 'miller miller)
(list 'smith smith))))
为了提升程序效率,可以去除不可能的数据并且嵌套 let 和 require:
(define (multiple-dwelling-2)
(let ((miller (amb 3 4 5)) ;miller > cooper
(cooper (amb 2 3 4 5))) ;not 1
(require (> miller cooper))
(let ((fletcher (amb 2 3 4))) ;not 1 and 5
(require (> (abs (- fletcher miller)) 1))
(let (smith (amb 1 2 3 4 5))
(require (not (= (abs (- smith fletcher)) 1)))
(let ((backer (amb 1 2 3 4))) ;not 5
(require (not (= (abs (- fletcher cooper)) 1)))
(require (distict?
(list baker cooper
fletcher miller smith)))
(list (list 'baker baker)
(list 'cooper cooper)
(list 'fletcher fletcher)
(list 'miller miller)
(list 'smith smith)))))))
如果我们需要使用普通 Scheme 程序来描述,可以这样做:第一种做法是生成所有可能解,然后逐个判断 multiple-dwelling-common 就是如此,第二种则更聪明一些,将楼层看做是数字的不同位,从末位开始,大于 5 则进位,从而提高了效率:multiple-dwelling-common-2 实现了它。
(define (enumerate-interval from to)
(if (> from to) '()
(cons from (range (+ from 1) to))))
(define (fold op init seq)
(define (iter result rest)
(if (null? rest) result
(iter (op result (car rest)) (cdr rest))))
(iter init seq))
(define (flatmap proc seq) (fold append '() (map proc seq)))
(define (unique-pairs)
(define all (enumerate-interval 1 5))
(flatmap (lambda (a)
(flatmap (lambda (b)
(flatmap (lambda (c)
(flatmap (lambda (d)
(map (lambda (e)
(list a b c d e))
all)) all)) all)) all)) all))
(define (multiple-dwelling-common)
;simple, quick answer by fucking machine
;backer 1 cooper 2 fletcher 3 miller 4 smith 5
(define role (lambda (x)
(define b (car x))
(define c (cadr x))
(define f (caddr x))
(define m (cadddr x))
(define s (car (cddddr x)))
(if (and (not (= b 5))
(not (= c 1))
(not (= f 5))
(not (= f 1))
(distict? x)
(> m c)
(not (= (abs (- s f)) 1))
(not (= (abs (- f c)) 1)))
;(> (abs (- f m)) 1))
(list 'find b c f m s)
(list 'drop b c f m s))))
(filter (lambda (x) (eq? (car x) 'find))
(map role (unique-pairs))))
(define (multiple-dwellings-common-2)
(define (house-iter b c m f s)
(cond ((> b 4) ; Baker can't live on 5th floor.
'(no answer available))
((> c 5)
(house-iter (+ b 1) 2 3 2 1))
((> m 5)
(house-iter b (+ c 1) (+ c 2) 2 1)) ; miller is above cooper
((> f 4) ; fletcher can't live on 5th floor
(house-iter b c (+ m 1) 2 1))
((> s 5)
(house-iter b c m (+ f 1) 1))
((and (not (= (abs (- s f)) 1))
(not (= (abs (- c f)) 1))
(distinct? (list b c m f s)))
(list (list 'baker b) (list 'cooper c)
(list 'fletcher f) (list 'miller m)
(list 'smith s)))
(else
(house-iter b c m f (+ s 1)))))
(house-iter 1 2 3 2 1)) ; initial values take some restrictions into account
对于下面的逻辑谜题而言,同样可以使用 amb 解决:

(define (score)
(let ((b (amb 1 2 3 4 5))
(distance (amb 1 2 3 4 5))
(a (amb 1 2 3 4 5))
(j (amb 1 2 3 4 5))
(m (amb 1 2 3 4 5)))
(require (or (and (= distance 2) (not (= b 3))
(and (not (= distance 2)) (= b 3)))))
(require (or (and (= j 3) (not (= a 5)))
(and (not (= j 3) (= a 5)))))
(require (or (and (= distance 2) (not (= m 4)))
(and (not (= distance 2) (= m 4)))))
(require (or (and (= m 4) (not (= b 1)))
(and (not (= m 4)) (= b 1))))
(distict? (list b distance a j m))
(list b distance a j m)))
甚至更加复杂的逻辑谜题也是一样,区别是,现在使用一般过程就变得非常棘手,而 amb 则始终能够将抽象控制在一个很高的层次:

(define (ship)
;1lor(?) -> more
;2mel(barn) -> col
;3ros -> hall
;4gab -> barn
;5mary(more) -> park
(let ((more (amb 5))
(barn (amb 2))
(col (amb 1 3 4))
(hall (amb 1 4))
(park (amb 1 3 4))
(require (distinct? (list col hall park)))
(require (cond ((= hall 4) (= park 3))
((= col 4) (= park 2))
(else false)))
(list 'more more
'barn barn
'col col
'hall hall
'park park))))
八皇后问题(将 8 个皇后放在 n * n 的棋盘上使得其彼此不在同一行、列对角线的解法)也是如此:
(define (queen n)
(define (can-setted col result)
(define (iter next distance)
(or (null? next)
(let ((setted (car next)))
(and (not (= col setted))
(not (= col (abs (- setted distance))))
(not (= col (abs (+ setted distance))))
(iter (cdr next) (+ distance 1)))))
(iter (car result 1)))
(define (iter row result)
(if (= row n) (display result)
(let ((col (an-integer-between 0 (- n 1))))
(require (can-setted col result))
(iter (+ row 1) (cons col result)))))
(iter 0 '()))
最后,我们来看使用 amb 解决自然语义分析这个非确定性的例子:
(define nouns '(noun student professor cat class))
(define verbs '(verb studies lectures eats sleeps))
(define articles '(article the a))
(define prepositions '(prep for to in by with))
(define adjectives '(adjective ugly stupid beauty lovely))
parse 读取文本,将其写入 unparsed 变量中,之后对句子每个单词进行解析:parse-sentence,直到结束,parse-sentence 本质就是通过 phrase-word 对特定字典进行检查,如果满足条件则返回对应字符和其此性,并将其从未检查的 unparsed 变量数据移除。parse-sentence 依赖 parse-noun-phrase 来解析冠词和名词,并组合动词组合为一种带有词性标记的数据结构。
(define *unparsed* '())
(define (parse input)
(set! *unparsed* input)
(let ((sent (parse-sentence)))
(require (null? *unparsed*))
sent))
(define (parse-word word-list)
(require (not (null? *unparsed*)))
(require (memq (car *unparsed*) (cdr word-list)))
(let ((found-word (car *unparsed*)))
(set! *unparsed* (cdr *unparsed*))
(list (car word-list) found-word)))
;(parse '(the cat eats))
;(sentence (noun-phrase (article the) (noun cat)) (verb eats))
(define (parse-noun-phrase) ;the cat
(list 'noun-phrase
(phrase-word articles)
(phrase-word nouns)))
(define (parse-sentence) ;(the cat) eats
(list 'sentence (parse-noun-phrase)
(phrase-word verbs)))
parse-word-gen 是一种用于替代 parse-word 的过程,其不对传入的单词进行词性检查和标记,而是(随机-这里没有实现随机,只是顺序获取,ramb 实现了随机获取,参见下文 amb 的实现)返回同词性的任一单词,以生成类似的句子。
(define (parse-word-gen word-list)
;for each need, take from word-list but ignore *unparsed*
(require (not (null? *unparsed*)))
(set! *unparsed* (cdr *unparsed*))
(list (car word-list) (amb (cdr word-list))))
现在我们想要扩大自然语言语法范围,加入介词和形容词,实现类似的效果:
;(parse '(this student with the cat sleeps in the class))
#| (sentence (noun-phrase
(simple-noun-phrase (article the) (noun student))
(prep-phrase (prep with)
(simple-noun-phrase
(article the) (noun cat))))
(verb-phrase
(verb sleeps)
(prep-phrase (prep in)
(simple-noun-phrase
(article the) (noun class))))) |#
其实现也不复杂,现在生成句子包含两部分:名词部分和动词部分,其中名词部分 parse-noun-phrase 包含 parse-simple-noun-phrase 解析简单冠词+名词的和带有 parse-prepositional-phrase 解析的带有介词拓展的部分。这里介词本质上就是一个介词短语+名词部分(注意不是简单名词,换言之,介词拓展可能包含递归的介词,这也是自然语言解析歧义性的来源之一)。其中动词部分也是类似,包含 parse-word 的动词本身以及可能带有介词拓展的动词(这是自然语言解析歧义性的来源之二)。
(define (parse-sentence)
;(the student with the cat) (sleeps in the class)
(list 'sentence (parse-noun-phrase)
(phrase-verb-phrase)))
(define (parse-simple-noun-phrase) ;the cat, the student
(list 'simple-noun-phrase
(parse-word articles)
(parse-word nouns)))
(define (parse-prepositional-phrase) ;with.., in...
(list 'prep-phrase (parse-word prepositions)
(parse-noun-phrase)))
(define (parse-noun-phrase) ;(the student) with (the cat)
(define (maybe-extend noun-phrase)
(amb noun-phrase
(maybe-extend (list 'noun-phrase
noun-phrase
(parse-prepositional-phrase)))))
(maybe-extend (parse-simple-noun-phrase)))
(define (parse-verb-phrase) ;(sleep) in (the class)
(define (maybe-extend verb-phrase)
(amb verb-phrase
(maybe-extend (list 'verb-phrase
verb-phrase
(parse-prepositional-phrase)))))
(maybe-extend (parse-word verbs)))
注意下面的 verb 解析方法是错误的,因为这里会陷入对于 verbs 的无穷循环,而不能正确扩展。如果要实现形容词支持,只需要修改 parse-simple-noun-phrase 改写为 with-adj 即可。
(define (parse-verb-phrase-2) ;错误,会陷入无穷循环
(amb (parse-word verbs)
(list 'verb-phrase
(parse-verb-phrase-2)
(parse-prepositional-phrase))))
(define (parse-simple-noun-phrase-with-adj) ;a beauty girl
(amb (list 'simple-noun-phrase
(parse-word articles)
(parse-word nouns))
(list 'simple-noun-phrase
(parse-word articles)
(parse-word adjectives)
(parse-word nouns))))
由于上面动词和介词解析的歧义性,所以自然语言解析需要使用 amb 非确定性求值,如下是一些例子。
;差别在于 parse-verb-phrase 是 parse-word 读入的 verb-phrase 是
;lectures to the student 还是 lectures
((snp (a the) (n processor))
(vp (vp (v lectures)
(pp (p to) (snp (a the) (n student))))
(pp (p with) ((a the) (n cat)))))
((snp (a the) (n processor))
(vp (v lectures)
(pp (p to) (np (snp ((a the) (n student)))
(pp (p with) (snp ((a the) (n cat))))))))
;差别来源于 parse-verb-phrase parse-word verbs 读入的动词到哪里结尾
;以及 parse-prepositional-phrase parse-word prepositions 读入的介词到哪里结尾
((the professor)
((lectures)
(to ((the student) (in ((the class) (with (the cat))))))))
((the professor)
((lecture (to the student))
((in the class) (with the cat))))
((the professor)
((lecture (to the student))
(in (the class (with the cat)))))
((the professor)
((lecture (to the student (in the class)))
(with the cat)))
((the professor)
((lecture ((to the student) (in the class)))
(with the cat)))
实现 amb 求值器
这里的 amb 求值器是基于带有语法分析的非惰性求值器改写而来的,换言之,如下代码需要基于一般求值器过程执行(这里提供了新的语法分析程序,加入了深度递归的支持):
根据我们的设计,需要为每个表达式执行引入除了 env 之外的两个参数:表达式执行成功时的回调和失败时的回调,如下所示,ambeval 是新改写的 eval,(analyze exp) 会返回解析的 lambda 表达式,传入这些参数以执行调用,其中成功回调包含两个参数,当前值和失败回调,这里的实例简单的为成功回调打印值,失败回调返回 'failed。
;for call amb exp lambda like eval
;成功继续是一个带有两个参数过程:当前待检验值和失败行为,
;如果值不满足 require 则调用无参的 fail 直接失败
; (ambeval <exp>
; the-global-environment
; (lambda (value fail) value)
; (lambda () 'failed))
(define (ambeval exp env succeed fail)
((analyze exp) env succceed fail))
时间循环函数现在支持 try-again,传入此指令意味着当前分支的失败,因此这里我们改写 internal-loop 加入 try-again 失败回调函数,在一开始传入空问题提示。在正常第一次调用时,会对表达式执行 ambeval 解析,这里成功的回调就是打印结果且继续等待输入,此时 try-again 已经被写入为失败时的回调函数了,当其被调用,会触发当前 amb 的失败以回退到上一个深度优先节点并继续,而 ambeval 解析失败的回调就是重新开始事件循环,即 amb 没有任何可用解。
;重新实现的 driver-loop 维持了当前状态信息:try-again
;ambeval 成功则自动进入下一个状态,try-again 调用也是
;如果全部失败则直接重新开始
(define (driver-loop)
(define (internal-loop try-again)
(display ">>")
(let ((input (read)))
(if (eq? input 'try-again)
(try-again)
(begin
(newline)
(display ";;; Starting a new problem ")
(ambeval input
the-global-environment
;成功则从下一次状态开始
(lambda (val next-alt)
(user-print val)
(internal-loop next-alt))
;失败直接重新开始,关闭状态
(lambda ()
(user-print input)
(driver-loop)))))))
(internal-loop
(lambda () (newline)
(display ";;; There is no current problem")
(driver-loop))))
analyze 过程如下所示,这里和之前大致类似,新加入了 if-fail? 和 amb? 与 ramb?
(define (analyze exp)
(cond ((self-evaluating? exp)
(analyze-self-evaluating exp))
((quoted? exp) (analyze-quoted exp))
((variable? exp) (analyze-variable exp))
((assignment? exp) (analyze-assignment exp))
((definition? exp) (analyze-definition exp))
((if? exp) (analyze-if exp))
((if-fail? exp) (analyze-if-fail exp))
((let? exp) (analyze-let exp))
((lambda? exp) (analyze-lambda exp))
((begin? exp) (analyze-sequence (begin-actions exp)))
((cond? exp) (analyze (cond->if exp)))
((amb? exp) (analyze-amb exp))
((ramb? exp) (analyze-ramb exp))
((application? exp) (analyze-application exp))
(else (error "Unknown expression type -- ANALYZE" exp))))
上面说到,try-again 会触发 amb 过程的 failure 回调函数,而其实现则如下所示:amb? 和 ramb? 实现了标签判断,amb-choices 实现了从可用 amb 值中顺序选择的能力,ramb-choices 实现了从可用的 amb 值中随机选择的能力。
;for check & select (amb <exp> <exp2>)
(define (amb? exp) (tagged-list? exp 'amb))
(define (ramb? exp) (tagged-list? exp 'ramb))
(define (amb-choices exp) (cdr exp)))
(define (ramb-choices exp)
(define (rand-list exp n)
(cond ((null? exp) exp)
((null? (cdr exp)) (car exp))
((= n 0) (car exp))
(else (rand-list (cdr exp) (- n 1)))))
(rand-list exp (random (length exp))))
analyze-amb 的过程很简单,首先对于所有可用项进行解释,得到 cprocs 值,然后对其首个进行调用,失败时继续 try-next 尝试下一个值,成功时返回成功回调(对于 REPL 而言成功就是等待下一个输入,失败会调用此处 try-next 直到成功或者没有可用值执行失败回调 f 即 REPL 定义的清空当前状态重新开始)。
;for gen amb expression lambda in analyzes
;; try all choices until success or else call failure continuation
(define (analyze-amb exp)
(let ((cprocs (map analyze (amb-choices exp))))
(lambda (env s f)
(define (try-next choices)
(if (null? choices) (f)
((car choices) env
s
(lambda () (try-next (cdr choices))))))
(try-next cprocs))))
(define (analyze-ramb exp)
(let ((cprocs (map analyze (ramb-choices exp))))
(lambda (env s f)
(define (try-next choices)
(if (null? choices) (f)
((car choices) env
s
(lambda () (try-next (cdr choices))))))
(try-next cprocs))))
注意这里成功和失败的选择完全由 require 过程是否返回 (amb) 来触发,对于 require 的执行,其始终在一个或多个 amb 之后,其创建了一个新的环境并开始执行 (if (not p) (amb)) 体,当 require 失败返回 (amb) 后 analyze-amb 根据 (if (null? choices) (f)) 调用环境中的 failure 回调,因为这里发生在 body 体中,因此 analyze-sequence 递归为每个表达式创建嵌套环境,这里 require 的 failure 回调就是离它最近的 amb 语句提供的 failure —— 当然,如果 p 的 amb 回调没有可用时:(if (null? choices) (f)) 其触发再上一层的 failure 回调,如果外层还有 amb 的话,会从这里继续获取值,如果全部失败,则返回最外层的 driven-loop 的失败回调:重置此问题:((define a (amb 1 2 3)) (define b (amb 4 5 6)) (require (= (+ a b) 100))。
当然,为了其他过程能配合 f 和 s 回调执行,这里都要进行修改,其中字面值、quote、变量、lambda 都调用 s 回调以返回原来的值(默认成功),而像 if、let、sequence 则需要对每个表达式分别处理,比如 analyze-if 返回的闭包执行谓词判断,如果成功则继续执行对应语句的分派,sequence 也是如此(这里 sequence 的嵌套闭包决定了 require 能起作用)。
;;always success
(define (analyze-self-evaluating exp)
(lambda (env s f) (s exp f)))
(define (analyze-quoted exp)
(let ((qval (text-of-quotation exp)))
(lambda (env s f) (s qval f))))
(define (analyze-variable exp)
(lambda (env s f) (s (lookup-variable-value exp env) f)))
(define (analyze-lambda exp)
(let ((vars (lambda-parameters exp))
(bproc (analyze-sequence (lambda-body exp))))
(lambda (env s f) (s (make-procedure vars bproc env) f))))
;;call each exp
(define (analyze-if exp)
(let ((pproc (analyze (if-predicate exp)))
(cproc (analyze (if-consequent exp)))
(aproc (analyze (if-alternative exp))))
(lambda (env s f)
(pproc env
(lambda (pred-value f2)
(if (true? pred-value)
(cproc env s f2)
(aproc env s f2)))
f))))
(define (if-fail? exp) (tagged-list? exp 'if-fail))
(define (analyze-if-fail exp)
(define if-exec (cadr exp))
(define if-fail (caddr exp))
(let ((pproc (analyze if-exec))
(fproc (analyze if-fail)))
(lambda (env s f)
(pproc env s (lambda () (fproc env s f))))))
(define (analyze-let exp)
(analyze-lambda (let->combination exp)))
(define (analyze-sequence exp)
(define (sequentially proc1 proc2)
(lambda (env s f)
(proc1 env
(lambda (proc1-value f2) (proc2 env s f2))
f)))
(define (loop first-proc rest-procs)
(if (null? rest-procs) first-proc
(loop (sequentially first-proc (car rest-procs))
(cdr rest-procs))))
(let ((procs (map analyze exps)))
(if (null? procs)
(error "Empty sequence -- ANALYZE" 233))
(loop (car procs) (cdr procs))))
对于定义和赋值则还要考虑到失败撤销的问题,这里的赋值先保存了旧变量值,如果失败,在执行失败回调前先重新赋值为旧值实现了撤销。考虑到有一些场景可能不需撤销,比如技术,引入 permanent-set! 特殊形式直接执行原来的失败回调,不重新赋值。
;if failed, rollback
(define (analyze-definition exp)
(let ((var (definition-variable exp))
(vproc (analyze (definition-value exp))))
(lambda (env s f)
(vproc env
(lambda (val f2)
(define-variable! var val env)
(s 'ok f2))
f))))
(define (analyze-assignment exp)
(define (permanent? exp)
(tagged-list? exp 'permanent-set!))
(let ((var (assignment-variable exp))
(vproc (analyze (assignment-value exp))))
(lambda (env s f)
(vproc env
(lambda (val f2)
(let ((old-value
(lookup-variable-value var env)))
(set-variable-value! var val env)
(s 'ok
(if (permanent? exp)
f2
(lambda ()
(set-variable-value! var
old-value
env)
(f2))))))
f))))
复杂过程的执行和之前类似,不过对于每个运算符的解析和获取现在都递归通过 get-args 执行。
;;get args with s/f continuation
(define (analyze-application exp)
(let ((fproc (analyze (operator exp)))
(aprocs (map analyze (operands exp))))
(lambda (env s f)
(fproc env
(lambda (proc f2)
(get-args aprocs
env
(lambda (args f3)
(execute-application
proc args s f3))
f2))
f))))
(define (get-args aprocs env s f)
(if (null? aprocs) (s '() f)
((car aprocs)
env
(lambda (arg f2)
(get-args (cdr aprocs)
env
(lambda (args f3)
(s (cons arg args) f3))
f2))
f)))
(define (execute-application proc args s f)
(cond ((primitive-procedure? proc)
(s (apply-primitive-procedure proc args) f))
((compound-procedure? proc)
((procedure-body proc)
(extend-environment (procedure-parameters proc)
args
(procedure-environment proc))
s f))
(else (error "Unknown procedure type -- EXECUTE-APPLICATION" proc))))
amb 解释器的一些扩展:ramb、permanent-set! 的实现在上面都看到了(ramb 在自然语言解析的随机生成中很好用,permanent-set! 可实现计数,下面左图是例子),上面还有一个 if-fail 的结构实现,其用途如下右图所示,可当全部失败时给出一个默认替代值(实际应用中非常好用)。

最后注意到,这里 require 的实现其实很有技巧,如果意识不到 require 可由用户过程表示,那么将不得不将 require 实现为一个特殊形式:
(define (require? exp) (tagged-list? exp 'requre))
(define (require-predicate exp) (cadr exp))
((require? exp) (analyze-require exp))
(define (analyze-require exp)
(let ((pproc (analyze (require-predicate exp))))
(lambda (env s f)
(pproc env
(lambda (v f2)
(if (not (true? v))
(f2)
(s 'ok f2))) f))))
逻辑程序设计
计算机科学处理命令式(怎么做)的知识,而数学则用于说明式(是什么)的知识,这一观点从第一章开始到现在为止大部分情况下都是成立的。但尽管大部分程序设计语言倾向于单一方向(清晰的输入和输出)的计算,我们也不能说“计算机程序 = 数据结构(数据抽象) + 算法(过程抽象)”代表了程序的全部,之前介绍的约束系统、上面介绍的非确定性求值器(包括数据查询语言 SQL)都不属于此类。本节将要实现一门数据查询语言,尽管 LISP 并不是实现这一目标的最佳方式,但是 LISP 提供的基本元素、基于基本元素的组合、抽象能力非常简洁和灵活,能让我们迅速打造出能表述及其复杂关系的查询语句,并使我们定义查询语言的表达能力更加强大。
数据查询语言用例
下面是一个人事数据库的断言,其中包含了各个员工的住址、工作、薪水、管理者,也包含了某种工作与其他工作的胜任关系。
(address (Bitdiddle Ben) (Slumerville (Ridge Road) 10))
(job (Bitdiddle Ben) (computer wizard))
(salary (Bitdiddle Ben) 60000)
(address (Hacker Alyssa P) (Cambridge (Mass Ave) 78))
(job (Hacker Alyssa P) (computer programmer))
(salary (Hacker Alyssa P) 40000)
(supervisor (Hacker Alyssa P) (Bitdiddle Ben))
(address (Fect Cy D) (Cambridge (Ames Street) 3))
(job (Fect Cy D) (computer programmer))
(salary (Fect Cy D) 35000)
(supervisor (Fect Cy D) (Bitdiddle Ben))
(address (Tweakit Lem E) (Boston (Bay State Road) 22))
(job (Tweakit Lem E) (computer technician))
(salary (Tweakit Lem E) 25000)
(supervisor (Tweakitlem E) (Bitdiddle Ben))
(address (Reasoner Louis) (Slumerville (Pine Tree Road) 80))
(job (Reasoner Louis) (computer programmer trainee))
(salary (Reason Louis) 30000)
(supervisor (Reasoner Louis) (Hacker Alyssa P))
(supervisor (Bitdiddle Ben) (Warbucks Oliver))
(address (Warbucks Oliver) (Swellesley (Top Heap Road)))
(job (Warbucks Oliver) (administration big wheel))
(salary (Warbucks Oliver) 150000)
(address (Scrooge Eben) (Weston (Shady Lane) 10))
(job (Scrooge Eben) (accounting chief accountant))
(salary (Scrooge Eben) 75000)
(supervisor (Scrooge Eben) (Warbucks Oliver))
(address (Cratchet Robert) (Allston (N Harvard Street) 16))
(job (Cratchet Robert) (accounting scrivener))
(salary (Cratchet Robert) 18000)
(supervisor (Cratchet Robert) (Scrooge Eben))
(address (Aull DeWitt) (Slumeerville (Onion Square) 5))
(job (Aull DeWitt) (administration secretary))
(salary (Aull DeWitt) 25000)
(supervisor (Aull DeWitt) (Warbucks Oliver))
(can-do-job (computer wizard) (computer programmer))
(can-do-job (computer wizard) (computer programmer trainee))
(can-do-job (administration secretary) (administration big wheel))
从最简单的查询开始,我们通过 (job ?x (computer programmer)) 来匹配工作是研发-开发者的所有员工,模式可包含多个变量,比如 (address ?x ?y) 也可以没有变量,同一模式变量可出现多次,比如 (supervisor ?x ?x) 表示上司是自己的员工,此外 (job ?x (computer ?type)) 用于捕获特定条目,而 (job ?x (computer . ?type)) 则用于将零个或多个字符捕获到 ?type 中(类似于 Scheme 变长语法),可匹配 (computer) (computer programmer) (computer programmer trainee)。
比如下面三条语句可以匹配 Ben 的下级、所有会计部的员工、所有居住在 Slumeerville 镇的员工。
(supervisor ?x (Bitdiddle Ben))
(job ?x (accounting . ?type))
(address ?x (Slumeerville . ?addr))
现在,让我们引入 and、or 和 not 来实现复合查询,为了支持普通 LISP 过程,这里额外提供了 list-value 形式以对数据进行 Scheme 过程的判断。比如下面三个语句实现了查找 BenBitdiddle 所有下属以及其住址、工资少于 BenBitdiddle 的人和其工资以及 BenBitdiddle 的工资、所有不是研发部门人管理的人以及其上司和工作。
(and (address ?person ?address)
(supervisor ?person (Bitdiddle Ben)))
(and (salary ?person ?salary)
(salary (Bitdiddle Ben) ?target)
(lisp-value < ?salary ?target))
(and (job ?person ?job)
(supervisor ?person ?boss)
(not (job ?boss (computer . ?others))))
接下来让我们定义抽象,rule 形式用于给定一条具名规则,其可以包含复合查询和简单查询,甚至是递归,比如 same 返回两个值的相等性,wheel 判断是否是大人物(两层领导),live-near? 用来判断两个人是否住的近(live-near-ordered? 去除了重复),outranked-by? 用于判断两个人是否存在层级关系,包括一层或多层,这里使用了递归。
(rule (same ?x ?x))
(rule (wheel ?person)
(and (supervisor ?middle-manager ?person)
(supervisor ?x ?middle-manager)))
(rule (live-near? ?p1 ?p2)
(and (address ?p1 (?town . ?rest1))
(address ?p2 (?town . ?rest2))
(not (same ?p1 ?p2))))
(live-near? ?x (Bitdiddle Ben))
(rule (live-near-ordered? ?p1 ?p2)
(and (address ?p1 (?town . ?rest1))
(address ?p2 (?town . ?rest2))
(lisp-value gt-person? ?p1 ?p2)))
(define (gt-person? p1 p2)
(define (p->s p)
(if (null? p) ""
(string-append
(symbol->string (car person))
(p->s (cdr person)))))
(string>? (p->s p1) (p->s p2)))
(rule (outranked-by? ?staff-person ?boss)
(or (supervisor ?staff-person ?boss)
(and (supervisor ?staff-person ?middle-manager)
(outranked-by ?middle-manager ?boss))))
下面的过程实现了两个人是否可互相替换的检查(新人应该能胜任旧人的工作),以及利用此过程实现了能工作替换且工资更低的人的查找。
(rule (replace? ?person ?new-person)
((or (and (job ?new-person ?work)
(job ?person ?work)
(not (same ?person ?new-person)))
(and (job? ?new-person ?other-work)
(can-do-job ?other-work ?work)
(job ?person ?work)
(not (same ?person ?new-person))))))
(replace? (Fect Cy D))
(and (salary ?p1 ?s1)
(salary ?p2 ?s2)
(lisp-value > s1 s2)
(replace? ?p1 ?p2))
下列过程实现了对于在本部门没有领导者的人的检查:
(rule (dep-boss? ?p)
(not (and (job ?p (?dep . ?rest1))
(supervisor ?p ?p2)
(job ?p2 (?dep . ?rest2)))))
这套系统可以任意扩展,比如实现会议记录以及会议记录查询:
(meeting accounting (Monday 9am))
(meeting administraton (Monday 10am))
(meeting computer (Wednesday 3pm))
(meeting administraton (Friday 1pm))
(meeting whole-company (Wednesday 4pm))
;查询周五是否有会议
(meeting ?dep (Friday ?time))
;查询某人在某天某个时间是否有会议(时间省略则查询天)
(rule (meeting-time ?person ?day-and-time)
(and (job ?person (?dep . ?rest))
(or (meeting ?dep ?day-and-time)
(meeting? whole-company ?day-and-time))))
(meeting-time (Hacker Alyssa P) (Thursday ?time))
这种基本形式、组合与抽象的能力使得我们可以将逻辑看做程序,比如 (append-to-form x y z) 可以表示为两条规则:(rule (a () ?y ?y) 任何和空结合的值是它自身,(rule (a (?u . ?v) ?y (?u . ?z)) (a ?v ?y ?z)) 如果 v 和 y 结合生成了 z,那么 (?u . ?v) 和 ?y 结合会生成 (?u . ?z)。基于此我们可以打破单向计算规则,实现反向计算,如下所示(当然,在复杂的情况下,这种反向计算可能失败)。

也比如下面的 next-to 规则可用于反向生成可能性:
(rule (?x next-to ?y in (?x ?y . ?u)))
(rule (?x next-to ?y in (?v . ?z))
(?x next-to ?y in ?z))
(?x next-to ?y in (1 (2 3) 4))
;;((2 3) next-to 4 in (1 (2 3) 4))
;;(1 next-to (2 3) in (1 (2 3) 4))
(?x next-to 1 in (2 1 3 1))
;;(3 next-to 1 in (2 1 3 1))
;;(2 next-to 1 in (2 1 3 1))
也比如下面的 last-pair 用于返回列表最后的 cons,我们可以基于如下定义实现匹配,注意并不是所有匹配都有解,比如 (last-pair ?x (3)),这会导致无穷循环。
(rule (last-pair (?x) (?x)))
(rule (last-pair (?first . ?rest) (?x))
(last-pair ?rest (?x)))
(last-pair (3) ?x) ;;(last-pair (3) (3))
(last-pair (1 2 3) ?x) ;;(last-pair (1 2 3) (3))
(last-pair (2 ?x) (3)) ;;(last-pair (2 3) (3))
(last-pair ?x (3)) ;;a lot
此外,我们可以实现逻辑语言的 reverse(脆弱的,(reverse (1 2 3) ?x) 会导致无穷循环:左右震荡,但 (reverse ?x (1 2 3) 将得到正确结果:reverse 右边始终是值):
(rule (reverse ?x ?y)
(and (append-to-form (?first) ?rest ?x)
(append-to-form ?rev-rest (?first) ?y)
(reverse ?rest ?rev-rest)))
最后,我们伪造了一个血缘关系表,可创建规则追踪儿子鉴定(某人的儿子或某人妻子的儿子)、孙子鉴定(某人的儿子的儿子)以及无穷尽的重孙鉴定:
(son Adam Cain)
(son Cain Enoch)
(son Enoch Irad)
(son Irad Mehujael)
(son Mehujael Methushael)
(son Methushael Lamech)
(wife Lamech Ada)
(son Ada Jabal)
(son Ada Jubal)
(rule (is-son ?a ?b)
(or (son ?b ?a)
(and (wife ?b ?x)
(son ?x ?a))))
(rule (grandson ?a ?b)
(and (is-son ?a ?x)
(is-son ?x ?b)))
(rule ((great . ?rel) ?x ?y)
(and (is-son ?x ?b)
(?rel ?b ?y)))
;((great grandson) ?g ?ggs)
;((great great grandson) ?g ?ggs)
;((great great great grandson) ?g ?ggs)
查询系统工作原理
有多种方式实现这一查询系统,比如使用上面介绍的 amb 求值器(解释器内部的深度优先遍历,参考实现,这一实现不太满足查询的逻辑,每次需要 try-again 获取下一条数据,除此之外,实现上基本就是将查询、合一和复合语句实现为 analyze 的分派,如果失败从数据库流中获取下一个满足条件的来操作),或者基于流。这里考虑基于流的实现:为了完成对断言(数据库数据条目,即这里的表)的匹配,这里不断的输入空环境,然后进行断言的模式匹配(为变量 ? 匹配表特定元素),如果匹配成功则意味着框架被扩充:环境内的变量 ? 被绑定并加入此框架,如果匹配不成功,则产生一个表明失败的特殊符号,其最后返回一个带有扩充的环境流,删除其中失败的信息,即得到所有满足条件的框架,其过程如下所示(类似于 eval 在表达式和环境之间的交互,不过 eval 是从环境获取变量绑定并更新表达式,而这里是将变量绑定添加到环境):
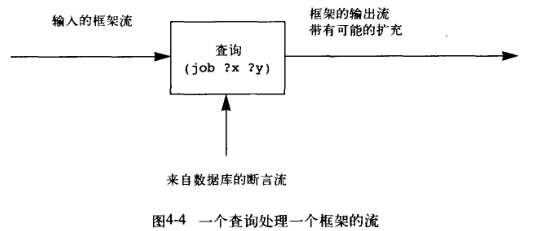
如果是复合查询,and 会让第一个接收匹配返回的框架流进入第二个匹配,最终产生满足 A 和 B 的匹配的框架流,or 会分别对数据库断言进行匹配,并组合为新的流。对于 not 而言,其像是一个过滤器,选择性输出那些标记失败的框架,对于 lisp-value 而言,其也是一个过滤器,不过将匹配的特定变量输入到 Scheme 的 apply 过程中判断并决定是否满足匹配并对框架流选择性输出。这里的复合查询很有 eval 派生表达式的味道。
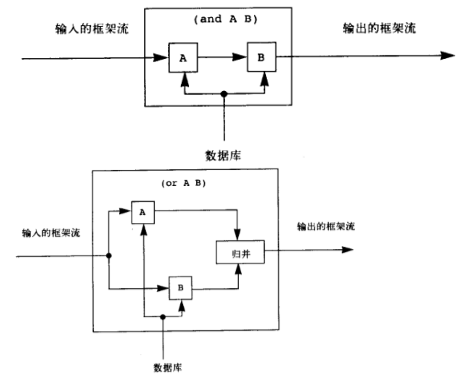
对于 rule 抽象而言,这种“模式匹配”不能起到很好的作用,我们需要一种称之为“合一”的机制,这一过程类似于 apply,即对于一条 rule 的定义将形参绑定到环境框架,然后对过程体在此框架中进行 eval 以产生对这个 rule 体的复合查询匹配的框架。考虑到基本查询和复合查询对应着基本元素和其组合,使用类似 eval 进行处理(环境绑定替换)也不足为怪,而 rule 作为数据查询语言的抽象,使用对类似过程定义的 apply 处理(扩展环境、展开抽象并进行 eval)也符合常理,这里并不是巧合,而是有深层次的必然。
因此,对于驱动循环而言,我们首先对框架进行模式匹配(基本元素,就像 eval 的基本过程 + - * /,对于查询语言而言,基本过程就是模式匹配),如果是特殊形式(and or not lisp-value)则进行分派(组合元素,对每个部分进行模式匹配),如果模式匹配找不到则使用合一器对规则进行展开(抽象元素),此外,为了区分断言和查询,现在使用 (assert! xxx) 来输入断言,其余情况将看做查询。
需要注意的是,这里的逻辑程序设计并不是数理逻辑,而是其中的子集。一方面,我们需要足够多的能力以足够描述可能希望去计算的问题,另一方面,我们又要求它足够的弱可以让我们有一种过程性的解释:说白了,逻辑程序设计的底层还是“如何做”的计算,不过现在我们通过元语言抽象将“是什么”和“怎么做”区分开,怎么做的知识由解释器提供。这种逻辑程序设计很有可能构造出低端低效的程序(类似于 SQL 内外层投影顺序),甚至是无穷循环,比如:(assert! (rule (married ?x ?y) (married ?y ?x)) 可处理 (married Mickey ?who) 的问题,但是却造成了无情循环,因为 rule 的参数匹配后,rule 的体又重新进行了自身的匹配。此外,我们程序中的 not 表示的是无法确定的含义,而非否的含义(在数理逻辑中包含了系统有所有知识的假设,因此 not 语义正确),因此,对于 (and (not (job ?x (computer programmer))) (supervisor ?x ?y)) 的查询,将导致第一个 not 对于空框架进行过滤,最终返回空(空框架能够满足 (job ?x (c p)) 的匹配,因为其还没有关于 ?x 的绑定,因此取反将导致返回空的流)—— 这里的解决办法是在解释 rule 的时候将 not 分派的语句移到最后去执行(Ex4.77)。
这里展示了一些脆弱程序的例子,如果将 outranked-by? 写成下面的顺序,将导致 and 子句无穷循环匹配。
(rule (outranked-by? ?staff-person ?boss)
(or (supervisor ?staff-person ?boss)
(and (supervisor ?staff-person ?middle-manager)
(outranked-by ?middle-manager ?boss))))
;if write like:
(rule (outranked-by? ?staff-person ?boss)
(or (supervisor ?staff-person ?boss)
(and (outranked-by ?middle-manager ?boss)
(supervisor ?staff-person ?middle-manager))))
而重复问题出现的概率也很高(这估计也是为啥 SQL 的 distinct 非常常用了吧),比如查找大人物,Warbucks Oliver 是四个人的经理,所以出现了四次,如果查找:(wheel ?who) 的话。这种重复问题导致了抽象建立很容易出现问题,比如 (sum ?amount (and (job ?x (c s)) (salary ?x ?amount))) 可以,但实现这个 sum 将无法处理像 wheel 返回的结果(因为有重复)。
下面展示了这一查询语言解释器的实现,首先是基本的流操作,这里进行了一些过程扩充,代码很简洁易懂。
;; 来自第三章的流实现:流定义、选择函数和基本过程
(define-syntax cons-stream
(syntax-rules () ((_ a b) (cons a (delay b)))))
(define (stream-car stream) (car stream))
(define (stream-cdr stream) (force (cdr stream)))
(define stream-null? null?)
(define the-empty-stream '())
(define (stream-ref s n)
(if (= n 0) (stream-car s)
(stream-ref (stream-cdr s) (- n 1))))
(define (stream-map proc s)
(if (stream-null? s) the-empty-stream
(cons-stream (proc (stream-car s))
(stream-map proc (stream-cdr s)))))
(define (stream-filter pred stream)
(cond ((stream-null? stream) the-empty-stream)
((pred (stream-car stream))
(cons-stream (stream-car stream)
(stream-filter pred
(stream-cdr stream))))
(else (stream-filter pred (stream-cdr stream)))))
(define (stream-for-each proc s)
(if (stream-null? s) 'done
(begin (proc (stream-car s))
(stream-for-each proc (stream-cdr s)))))
(define (display-line x) (display x) (newline))
(define (display-stream s) (stream-for-each display-line s))
(define (stream-enumerate-interval low high)
(if (> low high)
the-empty-stream
(cons-stream
low (stream-enumerate-interval (+ low 1) high))))
(define (stream-append s1 s2)
(if (stream-null? s1) s2
(cons-stream
(stream-car s1)
(stream-append (stream-cdr s1) s2))))
;; 额外增加的流操作
;;; stream-append-delayed 用于 append 流,第二个流作为后续
;;; interleave-delayed 用于 append 流,交替返回两个流内容
;;; stream-flatmap 用于将流打平,其交替为每个流进行打平操作
;;; singleton-stream 构建一个只包含一个元素的空流
(define (stream-append-delayed s1 delayed-s2)
(if (stream-null? s1)
(force delayed-s2)
(cons-stream
(stream-car s1)
(stream-append-delayed (stream-cdr s1) delayed-s2))))
(define (interleave-delayed s1 delayed-s2)
(if (stream-null? s1)
(force delayed-s2)
(cons-stream
(stream-car s1)
(interleave-delayed
(force delayed-s2)
(delay (stream-cdr s1))))))
(define (stream-flatmap proc s)
(define (flatten-stream stream)
(if (stream-null? stream)
the-empty-stream
(interleave-delayed
(stream-car stream)
(delay (flatten-stream (stream-cdr stream))))))
(flatten-stream (stream-map proc s)))
(define (singleton-stream x)
(cons-stream x the-empty-stream))
接下来我们定义界面(数据结构和 REPL 入口),对于查询的数据结构,这里提供 var? 判断是否是变量,constant-symbol? 判断是否为常量。对于复合查询数据结构,提供将形式和数据区分开来的 type 和 contents 过程。对于断言而言,也是如此。对于规则 rule 而言,提供判断谓词、获取规则头、规则体,这里提供了一个计数器方便我们对规则合一时对规则变量进行唯一的重命名(这里涉及的内容展开来讲比较复杂,涉及 LISP 和 Scheme 现代 LISP 开创性的词法作用域问题,如果想要避免重命名,一种方式是不再使用全局环境,而是使用类似于 Scheme 和一般解释器中使用的闭包和扩展框架,因为数据查询语言的核心在于数据且框架非常多,使用可扩展的框架搜索将导致效率降低,因此还是采用简单的重命名变量与全局环境比较好,参见 Daniel P. Friedman & David S. Wise 1976 的论文以及这篇文章链接)。
;查询数据结构,对于查询的每个元素,是否是变量: (? x) 或常量: (x)
(define (var? exp) (tagged-list? exp '?))
(define (constant-symbol? exp) (symbol? exp))
;复合查询数据结构:(and ??? ???) (or ??? ???)
(define (type exp)
(if (pair? exp) (car exp) (error "Unknown exp TYPE" exp)))
(define (contents exp)
(if (pair? exp) (cdr exp) (error "Unknown exp CONTENTS" exp)))
;断言数据结构:(assert! (address (Corkine Ma) WuHan GuanShan Road))
(define (tagged-list? exp tag)
(if (pair? exp) (eq? (car exp) tag) #f))
(define (assertion-to-be-added? exp)
(tagged-list? exp 'assert!))
(define (add-assertion-body exp)
(car (contents exp)))
;规则数据结构: (rule (same ?x ?y)) 和对于规则中变量重命名的过程: ?a ?3a
(define (rule? statement)
(eq? (car statement) 'rule))
(define (conclusion rule) (cadr rule))
(define (rule-body rule)
(if (null? (cddr rule))
'(always-true)
(caddr rule)))
(define rule-counter 0)
(define (new-rule-application-id)
(set! rule-counter (+ 1 rule-counter)))
(define (make-new-variable var rule-application-id)
;var: (? a), rule-application-id: x, return (? x a)
(cons '? (cons rule-application-id (cdr var))))
框架的实现和之前的环境类似,不过更简单一些,基本就是 key-value 的序对,暴力查找,提供了 extend 进行扩展的方法。对于底层数据库的实现和之前章节类似,这里额外提供了代码,本质就是一个二级表,提供 get 和 put API 传入 key1 key2 获取对应的值。
;绑定和框架数据结构:构造绑定、查找绑定值、在框架查找绑定、扩展框架
;binding: (var . val), frame: ((var . val) (var . val) (var . val))
(define (make-binding variable value) (cons variable value))
(define (binding-variable binding) (car binding))
(define (binding-value binding) (cdr binding))
(define (binding-in-frame variable frame)
(assoc variable frame))
(define (extend variable value frame)
(cons (make-binding variable value) frame))
;数据库基础表的实现
;('*table* (key1 (keya record) (keyb record2)) (key2 (keya record3)))
(define (make-table)
(let ((local-table (list '*table*)))
(define (lookup key-1 key-2)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record (cdr record) #f))
#f)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "Unknown operation -- TABLE" m))))
dispatch))
(define operation-table (make-table))
(define get (operation-table 'lookup-proc))
(define put (operation-table 'insert-proc!))
接着提供基于这个二层表的数据库实现,表格结构为 key:rule/assert:data,这里的 key 是传入表达式的 car,同一个 key 包含 rule 和 assertion 两张表,表保存的数据是流。注意,对于 rule 而言,其开头可能是 ?x 这种变量形式,此时使用 ? 这个 key 索引,当 fetch-rules 查找匹配规则时这些 ? 开头的也要算上。add-rule-or-assertion! 提供了根据输入将数据保存到规则还是断言表中的核心方法。
;从表格获取数据,表格结构为 key:rule-stream/assertion-stream:[data]
(define (get-stream key1 key2)
(let ((s (get key1 key2)))
(if s s the-empty-stream)))
(define (use-index? pat)
(constant-symbol? (car pat)))
;获取模式的首项,如果是变量则使用 ? 表示索引(专用于rule存储)
(define (index-key-of pat)
(let ((key (car pat))) (if (var? key) '? key)))
(define THE-ASSERTIONS the-empty-stream)
(define (fetch-assertions pattern frame)
(define (get-all-assertions) THE-ASSERTIONS)
(define (get-indexed-assertions pattern)
(get-stream (index-key-of pattern) 'assertion-stream))
(if (use-index? pattern) ;car 不是变量
(get-indexed-assertions pattern) ;返回所有头部常量匹配的
(get-all-assertions))) ;获取所有的断言
(define THE-RULES the-empty-stream)
(define (fetch-rules pattern frame)
(define (get-all-rules) THE-RULES)
;规则和断言不同,其开头可能是变量,其使用 ? 作为索引
(define (get-indexed-rules pattern)
(stream-append
(get-stream (index-key-of pattern) 'rule-stream)
(get-stream '? 'rule-stream)))
(if (use-index? pattern)
(get-indexed-rules pattern)
(get-all-rules)))
;将规则或断言添加到数据库
(define (add-rule-or-assertion! assertion)
;模式以常量符号或者变量 ? 开头
(define (indexable? pat)
(or (constant-symbol? (car pat))
(var? (car pat))))
(define (store-assertion-in-index assertion)
(if (indexable? assertion)
(let ((key (index-key-of assertion)))
(let ((current-assertion-stream
(get-stream key 'assertion-stream)))
(put key
'assertion-stream
(cons-stream assertion
current-assertion-stream))))))
(define (store-rule-in-index rule)
(let ((pattern (conclusion rule)))
(if (indexable? pattern)
(let ((key (index-key-of pattern)))
(let ((current-rule-stream
(get-stream key 'rule-stream)))
(put key
'rule-stream
(cons-stream rule
current-rule-stream)))))))
(define (add-assertion! assertion)
;这里之所以要用 let 将 THE-ASS 拿出来再放进去
;的理由是 (set! X (cons-stream N X)) 会有问题:
;因为不同于流中 (define X (cons-stream N X)) 的 X 为过程指针
;这里的 set! 直接修改 X 指针指向 (cons-stream N X),这里当获取
;X 的时候会永远获取到 N
(store-assertion-in-index assertion)
(let ((old-assertion THE-ASSERTIONS))
(set! THE-ASSERTIONS
(cons-stream assertion old-assertion))
'ok))
(define (add-rule! rule)
(store-rule-in-index rule)
(let ((old-rules THE-RULES))
(set! THE-RULES (cons-stream rule old-rules))
'ok))
(if (rule? assertion)
(add-rule! assertion)
(add-assertion! assertion)))
query-driver-loop 是 REPL 的入口,这里需要将输入的 ?x 换为 ? x 的形式,方便我们查找和构造变量,但是在打印结果前还要替换回去。除此之外,这里做的事情就是简单的区分是否要插入断言、以及是否是一个查询。对于查询而言,传入空流,调用 qeval 执行查询,调用 instantiate 进行实例化并打印流。
;查询则插入数据库并继续,否则 qeval 求值并打印流
;这里尚未约束的变量要在打印前换回到原来的输入表示形式
(define (query-driver-loop)
;将输入转换的 ?x 转换为 (? x) 方便后续查找
(define (query-syntax-process exp)
(define (map-over-symbols proc exp)
(cond ((pair? exp)
(cons (map-over-symbols proc (car exp))
(map-over-symbols proc (cdr exp))))
((symbol? exp) (proc exp))
(else exp)))
(define (expand-quertion-mark symbol)
(let ((chars (symbol->string symbol)))
(if (string=? (substring chars 0 1) "?")
(list '?
(string->symbol
(substring chars 1 (string-length chars))))
symbol)))
(map-over-symbols expand-quertion-mark exp))
;将内部表示(未约束的模式)转换回打印用的正确形式
(define (contract-question-mark variable)
(string->symbol
(string-append "?"
(if (number? (cadr variable))
(string-append (symbol->string (caddr variable))
"-"
(number->string (cadr variable)))
(symbol->string (cadr variable))))))
(printf "\n>>> ")
(let ((q (query-syntax-process (read))))
(cond ((assertion-to-be-added? q) ;如果是断言则插入数据库
(add-rule-or-assertion! (add-assertion-body q))
(display "Assertion added to database")
(query-driver-loop))
(else ;否者就需要 qeval 读入的查询,然后将结果实例化并输出
;(display output-prompt)
(display-stream
(stream-map
(lambda (frame)
(instantiate
q frame (lambda (v f) (contract-question-mark v))))
(qeval q (singleton-stream '()))))
(query-driver-loop)))))
实例化指的是将变量替换为环境中的绑定,如果遇到没有绑定的,进行特殊处理。
;为查询 q: (exp exp ..) 的每个元素 exp 在框架 frame 中查找并进行绑定
;如果遇到没有绑定的,使用 unbound-var-handler 进行处理:(? x) -> ?x
(define (instantiate exp frame unbound-var-handler)
(define (copy exp)
(cond ((var? exp) ;如果当前元素为变量,通过 binding-in-frame
;进行查找,如果找到则获取绑定值(绑定值可能还是一个变量,因此
;这里递归进行处理),如果找不到则调用找不到的处理器
(let ((binding (binding-in-frame exp frame)))
(if binding
(copy (binding-value binding))
(unbound-var-handler exp frame))))
((pair? exp) ;如果当前元素为序对,对其每个部分进行递归处理
(cons (copy (car exp)) (copy (cdr exp))))
(else exp))) ;无需实例化,直接返回
(copy exp))
qeval 是执行查询的核心过程,这里通过数据分派的方式实现了对于复合查询的支持,conjoin, disjoin 等,不管如何,其最终都是要执行 simple-query。
;核心过程,传入框架流,对 query 进行匹配,返回被 query 扩充过的框架流
(define (qeval query frame-stream)
;这里首先查找根据查找的 car 尝试进行分派(and, or, not 等)
;如果有分派,则使用分派过程来处理: conjoin, disjoin, negate, lisp-value
;如果没有分派,则调用 simple-query 进行处理:简单查询 or rule 合一
(let ((qproc (get (type query) 'qeval)))
(if qproc
;qproc 过程的执行参见下文 conjoin, disjoin, negate, lisp-value
(qproc (contents query) frame-stream)
;不论是分派无法找到的还是分派找到的,最终都会进入到这里(分派
;是对简单查询的组合,其本质还是要为每个简单查询调用 qeval)
;因此这里的 simple-query 才是查询器的核心过程
(simple-query query frame-stream))))
;数据导向分派支持 and 查询
(define (conjoin conjuncts frame-stream)
;递归对 and 查询的每个子查询调用 qeval,返回最终框架
;(and q1 q2) -> (qeval q2 (qeval q1 f-init))
(define (empty-conjunction? exps) (null? exps))
(define (first-conjunct exps) (car exps))
(define (rest-conjuncts exps) (cdr exps))
(if (empty-conjunction? conjuncts)
frame-stream
(conjoin (rest-conjuncts conjuncts)
(qeval (first-conjunct conjuncts)
frame-stream))))
;数据导向分派支持 or 查询
(define (disjoin disjuncts frame)
;对 or 查询的每个子查询调用 qeval,最后合并为新的流框架
;这里的合并不使用 stream-append 而是 interleave-delayed
;以便于每个子查询能轮流输出
(define (empty-disjunction? exps) (null? exps))
(define (first-disjunct exps) (car exps))
(define (rest-disjuncts exps) (cdr exps))
(if (empty-disjunction? disjuncts)
the-empty-stream
(interleave-delayed
(qeval (first-disjunct disjuncts) frame-stream)
(delay (disjoin (rest-disjuncts disjuncts)
frame-stream)))))
;数据导向分派支持 not 查询
(define (negate operands frame-stream)
;对框架流的每个框架检查,如果当前 query qeval 为空,则重新包含反之则置为空
(define (negated-query operands) (cadr operands))
(stream-flatmap
(lambda (frame)
(if (stream-null? (qeval (negated-query operands)
(singleton-stream frame)))
(singleton-stream frame)
the-empty-stream))
frame-stream))
;数据导向分派支持 list-value 查询
(define (lisp-value call frame-stream)
;对于原始框架流的每个框架进行如下处理:
;将当前 call 作为查询,当前 frame 作为框架进行实例化,如果实例化失败
;则直接报错,因为 lisp-value 不允许出现 frame 尚未绑定的变量
;实例化(绑定变量)后类似 (bigger? 3 2) 交给 execute
;后者先对程序进行实例化 - eval,然后加上参数交给 apply 执行。
;如果执行结果返回 #t,那么将当前框架返回,反之返回空框架
(define (execute exp)
(define (predicate exps) (car exps))
(define (args exps) (cdr exps))
;(apply (eval (predicate exp) user-initial-environment) (args exp)))
(apply (eval (predicate exp)) (args exp)))
(stream-flatmap
(lambda (frame)
(if (execute (instantiate call frame (lambda (v f)
(error "Unknown pat var -- LISP_VALUE" v))))
(singleton-stream frame)
the-empty-stream))
frame-stream))
;数据导向分派的一种特例,对于任何输入,始终返回框架
(define (always-true ignore frame-stream) frame-stream)
(put 'and 'qeval conjoin)
(put 'or 'qeval disjoin)
(put 'not 'qeval negate)
(put 'lisp-value 'qeval lisp-value)
(put 'always-true 'qeval always-true)
simple-query 是查询过程的核心,其使用 find-assertions 查找断言并扩充框架,最后实例化并打印。如果无法找到断言,则可能是规则,因此通过 apply-rules 查找规则并进行合一过程,再交给 qeval 进行 rule 体的复合表达式的绑定。为了体现层次结构,这里使用了局部过程,相关注解非常详细,注意要考虑的多种细节(比如合一的 depends-on?),以及这种复杂性如何通过递归优雅的实现(比如 pattern-match)。
;上述的入口和可扩展机制类似于 eval,而这里的 simple-query 则类似于 apply
;(包括基本过程的处理和复杂过程的处理 - 对应这里的 pattern-match 和 unify-match)
;对于框架流的每个框架进行查询匹配(find-assertions),返回扩充过的框架流(apply-rules)
(define (simple-query query-pattern frame-stream)
(define (find-assertions pattern frame)
;核心 API 的核心过程,用于对断言和查询进行 frame 下的匹配
(define (pattern-match pat dat frame)
;查找当前变量在框架中是否有绑定,如果没有则 extend 扩充当前框架
;如果有,则将当前变量替换为其值并继续尝试(不直接失败的原因是可能这个
;值也是一个变量或者包含变量的序对,比如 ?x -> (3 ?y)
(define (extend-if-consistent var dat frame)
(let ((binding (binding-in-frame var frame)))
(if binding
(pattern-match (binding-value binding) dat frame)
(extend var dat frame))))
;配合 (and (pair? pat) (pair? dat))
(cond ((eq? frame 'failed) 'failed)
;匹配到一个完全一致断言,直接返回此框架,无需扩充
((equal? pat dat) frame)
;遇到变量,则调用 extend-if-consistent 对当前变量进行扩充
((var? pat) (extend-if-consistent pat dat frame))
;如果当前元素是序对,递归进行处理(即先处理头部元素,试图将其作为扩充后的框架)
;如果失败,在 cond 头部即可匹配到,直接失败
((and (pair? pat) (pair? dat))
(pattern-match (cdr pat)
(cdr dat) (pattern-match (car pat) (car dat) frame)))
(else 'failed))) ;其他情况,直接失败
;使用 pattern-match 对数据库传入断言 assertion 和查询模式 query-pat 在 query-frame 下
;进行检查,如果满足要求,则返回扩充过的流,反之返回空流
(define (check-an-assertion assertion query-pat query-frame)
(let ((match-result
(pattern-match query-pat assertion query-frame)))
(if (eq? match-result 'failed)
the-empty-stream
(singleton-stream match-result))))
;fetch-assertions 查找 pattern car 匹配的所有断言,然后针对每一条断言
;执行 check-an-assertion 进行检查
(stream-flatmap (lambda (datum)
(check-an-assertion datum pattern frame))
(fetch-assertions pattern frame)))
;如果简单查询失败(为空)则可能意味着是一个规则,需要进行合一
(define (apply-rules pattern frame)
(define (unify-match p1 p2 frame)
;和 extend-if-consistent 类似,这里先通过 binding-in-frame 查找当前变量
;是否存在绑定,如果有,那么递归进行 unify-match 去处理(扩展 or 继续绑定)
;在递归得到扩展之前(走到 extend 分支)还需要进行两种检查:
;①如果待匹配目标 val 也是变量,那么就在框架查找它是否有约束的值
;如果有,则使 var 约束到这个绑定而非变量 val,如果没有,则使 var 绑定到 val。
;②如果待匹配目标 val 和 var 之间互相依赖(depends-on?),那么直接失败。
(define (extend-if-possible var val frame)
;递归查找当前待匹配目标 val 是否和 var 互相依赖
(define (depends-on? exp var frame)
(define (tree-walk e)
(cond ((var? e)
(if (equal? var e) #t ;val 和 var 完全一致,直接返回
;从框架查找 val 变量绑定,如果找不到,则意味着没有依赖
;如果找到,那么递归为找到的值查找依赖
(let ((b (binding-in-frame e frame)))
(if b (tree-walk (binding-value b)) #f))))
((pair? e) ;如果是序对,则对每个元素分别进行依赖查找
(or (tree-walk (car e))
(tree-walk (cdr e))))
(else #f)))
(tree-walk exp))
(let ((binding (binding-in-frame var frame)))
(cond (binding (unify-match (binding-value binding) val frame))
((var? val)
(let ((binding (binding-in-frame val frame)))
(if binding
(unify-match var (binding-value binding) frame)
(extend var val frame))))
;不允许 (?x ?x) -> (?y <xx ?y>)
((depends-on? val var frame) 'failed)
(else (extend var val frame)))))
;类似于 pattern-match 过程,不过遇到变量进入 extend-if-possible继续检查
(cond ((eq? frame 'failed) 'failed)
((equal? p1 p2) frame)
((var? p1) (extend-if-possible p1 p2 frame))
((var? p2) (extend-if-possible p2 p1 frame))
((and (pair? p1) (pair? p2))
(unify-match (cdr p1) (cdr p2)
(unify-match (car p1) (car p2) frame)))
(else 'failed)))
;对规则 rule,首先要将其整体变量重命名(避免和 query 冲突),然后
;调用 unify-match 对 rule 的头进行匹配得到扩充过的框架流,
;此过程失败,则返回空流
;成功则将 rule 的体(复合query)用扩充过的框架流 qeval 继续进行匹配。
(define (apply-a-rule rule query-pattern query-frame)
(define (rename-variables-in rule)
(let ((rule-application-id (new-rule-application-id)))
(define (tree-walk exp)
(cond ((var? exp)
(make-new-variable exp rule-application-id))
((pair? exp)
(cons (tree-walk (car exp))
(tree-walk (cdr exp))))
(else exp)))
(tree-walk rule)))
(let ((clean-rule (rename-variables-in rule)))
(let ((unify-result
(unify-match query-pattern
(conclusion clean-rule)
query-frame)))
(if (eq? unify-result 'failed)
this-empty-stream
(qeval (rule-body clean-rule)
(singleton-stream unify-result))))))
;合一和应用模式匹配类似,先通过 fetch-rules 找到所有 rules
;(包括 car pattern 开头的和 ? 开头的),然后对每条规则进行
;apply-a-rule
(stream-flatmap (lambda (rule)
(apply-a-rule rule pattern frame))
(fetch-rules pattern frame)))
;对传入的框架流每一个框架分别执行如下两个过程,生成两个流并合并:
;查找数据库中复合 query 查询模式的断言
;如果找不到断言,则可能是一条 rule,需要进行合一过程
(stream-flatmap
(lambda (frame)
(stream-append-delayed
(find-assertions query-pattern frame)
(delay (apply-rules query-pattern frame))))
frame-stream))
这里分派 and 的实现效率很低,对于第一个简单语句,扫描数据库执行后得到的每个扩充的框架都要逐个框架重新扫描数据库给第二个匹配,依次类推,这将导致严重的问题。另一种方法是对每个简单语句都执行匹配,找到相容的框架并进行合并,下面的过程进行了实现:join-frame 对两个框架进行检查如果相容则进行合并,conjoin-2 对每个语句产生的框架流都执行了这种合并,以产生满足所有需求的情况。
(define (conjoin-2 conjuncts frame-stream)
(define (empty-conjunction? exps) (null? exps))
(define (first-conjunct exps) (car exps))
(define (rest-conjuncts exps) (cdr exps))
(if (empty-conjunction? conjuncts)
frame-stream
(stream-map join-frame
(qeval (first-conjunct conjuncts) frame-stream)
(conjoin-2 (rest-conjuncts conjuncts) frame-stream))))
(define (join-frame f1 f2)
(define (good? var val target-frame)
(let ((binding (binding-in-frame var target-frame)))
(cond (binding
(let ((bind-val (binding-value binding)))
(if (var? bind-val)
(good? bind-val val target-frame)
(equal? val bind-val))))
(else #t))))
(if (null? f1) f2
(let ((head (car f1))
(if (good? (binding-variable head)
(binding-value head) f2)
(join-frame (cdr f1) (cons head f2))
'failed)))))