SICP 104 - 模块化、状态和对象
这是 SICP 第三章的内容总结,包含了全部习题的答案。本文阐述了使用赋值和局部状态实现更好的模块化,探讨了这种模型在模拟真实物体上的优势,以及这种为代码引入“时间维度”带来的后果:对于同一和变化、引用透明性和把握代码的时序性导致的心智负担等问题,尤其在并发模型下的严重水土不服。作为替代,我们引入了同样可以表示状态的流模型,通过对流模型的概念和应用的审视来探索其适用范围,并最终得出结论:当非共享状态大于共享时,对象可更好的实现模块化,反之基于函数式(非赋值)和流模型则更方便。
赫拉克里克说:即使在变化中,它也丝毫未变。Alphonse Karr 说:变得越多,它就越是原来的样子。
应对大型系统的复杂性,抽象很重要,不过这还不够,我们还需要模块化策略。模块化通常要求程序基于被模拟系统的结构来进行设计,物理系统的对象对应着计算对象,系统的活动对应着符号操作,这种方式允许我们在扩充新对象和新活动时不必对程序进行全面的修改,只需要添加新的代码即可(工作在局部)。一般而言,大型程序的组织有两个通路:第一种关注对象,将一个系统看做一大批对象,使用计算的环境模型,对象的行为随着时间变化,在映射被模拟系统的结构上存在着天然的对应。第二种关注信息流,使用计算的代换模型,流方式将我们从时间的枷锁中解脱出来,在并发执行程序上有着更好的兼容性。不论什么通路,模块化中总体现了数据抽象和过程抽象,不过侧重点并不相同,简单来说,关注对象的策略扩展了程序的时间维度,简化了模型,但因为引入状态而损失了数据抽象和过程抽象能力,而关注信息流的策略过程坚若磐石,缺点是模型复杂,但无状态的特征使其可具备较高的数据抽象和过程抽象能力。
赋值和局部状态
可以很容易的实现 Java 类似的类和对象:让函数返回一个函数,后者包含一个闭包以包含内部对象,通过 set! 来修改内部对象实现字段,begin 在这里执行多个表达式,返回最后一个,类似于 let。在返回这个函数中,从参数获取操作符,分派给内部过程以实现方法(这个例子和 JavaScript 高级程序编程中那些通过闭包构造对象的奇淫技巧类似,可见 JavaScript 和 Lisp 的渊源)。广义来讲,我们将广泛采用赋值的程序设计称之为命令式程序设计,而将不使用任何赋值的程序设计称之为函数式程序设计。
下面提供了一个带密码的支持存取款的银行实现,除了存款,输入密码错误次数也是变量,超出 7 次后自动报警。
;局部状态变量
(define (bank secret account)
(let ((retry 7))
(define (call-the-cops)
(begin (set! retry 0) (printf "CALLING 110 NOW...\n")))
(define (store money)
(begin (set! account (+ account money)) account))
(define (take money)
(let ((rest (- account money)))
(if (< rest 0)
(begin (printf "Not enough money in your account") -1)
(begin (set! account rest) rest))))
(define (dispatch pass method . args)
(cond ((not (and (symbol? pass) (eq? pass secret)))
(begin (set! retry (- retry 1))
(if (< retry 0) (call-the-cops))
(printf "Error password, retry ~d\n" retry) -1))
((eq? method 'store) (apply store args))
((eq? method 'take) (apply take args))
(else (error "no support method" method))))
(if (symbol? secret) dispatch (error "not a valid password" secret))))
(define jane (bank '123456wp 100))
(printf "~s\n" (jane '1234 'take 100))
(printf "~s\n" (jane '123456wp 'store 100))
(printf "~s\n" (jane '123456wp 'take 500))
(printf "~s\n" (jane '123456wp 'take 10))
下面是一个累加器的实现,通过此对象可实现值累加(state 在此处作为闭包中的变量):
(define (make-accumulator state)
(lambda (new-number)
(begin (set! state (+ state new-number)) state)))
(define A (make-accumulator 5))
(printf "~s ~s\n" (A 10) (A 10))
下面是一个函数调用监控器,支持查询调用此处和重置调用此处,可以看到局部状态在某些情况下确实很有用:
(define (make-monitored f)
(let ((count 0))
(lambda (command)
(cond ((eq? command 'how-many-calls?) count)
((eq? command 'reset-count) (set! count 0))
(else (begin (set! count (+ count 1))
(f command)))))))
(define s (make-monitored sqrt))
(printf "~d ~d\n" (s 'how-many-calls?) (s 100))
赋值带来了很多好处,其中一个典型就是随机数生成器,rand-update 是基于典型算法实现的随机数生成器,但其并不好用,因为要随时记住生成的值并下次使用时将其作为参数传入。random-init 调用时钟返回一个随机的初始值。
;赋值带来的利益
(define (rand-update x)
(let ((a 233) (b 234) (m 13))
(mod (+ (* a x) b) m)))
(define (random-init) (date-nanosecond (current-date)))
estimate-pi 使用蒙特卡洛方法来求 π 值,因为 6/(π*π) 是随机选取的两个整数间没有公共因子(最大公因子为 1)的概率,因此 rand 可重复 trials 次,最后通过概率求 π。
(define (estimate-pi trials)
;6/(π*π) 是随机选取两个整数间没有公共因子的概率
(define rand
(let ((x random-init))
(lambda () (set! x (rand-update x)) x)))
(define (cesaro-test)
(= (gcd (rand) (rand)) 1))
(define (monte-carlo trials experiment)
(define (iter trials-remaining trials-passed)
(cond ((= trials-remaining 0)
(/ trials-passed trials))
((experiment)
(iter (- trials-remaining 1) (+ trials-passed 1)))
(else (iter (- trials-remaining 1) trials-passed))))
(iter trials 0))
(sqrt (/ 6 (monte-carlo trials cesaro-test))))
不引入赋值将会引起程序的复杂化,这里还仅仅是一个变量就已经导致了 monte-carlo 不能独立为一个通用过程的结果。
(define (estimate-pi-2 trials)
(define (random-gcd-test trials initial-x)
(define (iter trials-remaining trials-passed x)
(let ((x1 (rand-update x)))
(let ((x2 (rand-update x1)))
(cond ((= trials-remaining 0)
(/ trials-passed trials))
((= (gcd x1 x2) 1)
(iter (- trials-remaining 1)
(+ trials-passed 1) x2))
(else (iter (- trials-remaining 1)
trials-passed x2))))))
(iter trials 0 initial-x))
(sqrt (/ 6 (random-gcd-test trials random-init))))
计算 π 的另一种方法是通过模拟估计定积分来求 π,对于一个矩形,其中有一个圆,那么矩形中的点随机落到圆中的概率就是圆的面积和矩形面积的比值。
(define (estimate-integral p x1 x2 y1 y2 trials)
(define (random-in-range low high)
(let ((range (- high low)))
(+ low (random range))))
(define circle-x (+ (/ (- x2 x1) 2) x1))
(define circle-y (+ (/ (- y2 y1) 2) y1))
(define (double x) (* x x))
(define (integral)
(let ((x (random-in-range x2 x1))
(y (random-in-range y2 y1)))
(not (> (+ (double (- x circle-x))
(double (- y circle-y)))
(double 1)))))
(* (- x2 x1) (- y2 y1) (monte-carlo trials integral)))
一些时候,我们可能希望重置随机数生成器,下面的 rand 实现利用赋值和局部变量实现了这一点:
(define (rand)
(let ((init (random-init)))
(lambda (command . values)
(cond ((eq? command 'generate)
(begin (set! init (rand-update init)) init))
((eq? command 'reset) (set! init (car values)))))))
(define r (rand))
(r 'reset 233)
(printf "~s ~s\n" (r 'generate) (r 'generate))
(r 'reset 233)
(printf "~s ~s\n" (r 'generate) (r 'generate))
总的来说,与所有状态显式的操作和传递额外参数相比,引入赋值和将状态隐藏在局部变量中的技术让我们以一种更加模块化的方式打造系统。但引入状态,扩展程序的时间维度也是具有代价的。
环境模型的代价主要体现在:因为引入了局部状态,计算的代换模型现在失效了 —— 代换的基础:符号作为值的名字不再存在,在引入局部状态的情况下,一个变量不再是一个名字,而是一个存储着值的内存位置,这里的值可以改变。这意味着对于一个过程,在不同时间调用可能有不同的结果(换言之,代码不再永恒)。代换模型失效的代价影响非常深远,最典型的就是同一和变化问题。将同一的东西可互相替换称之为引用透明性,在代换模型中同一非常容易理解,而在环境模型中,同一的意义则较为棘手,假如有两个账户,同一的第一层意义是两个人共用账户,即引用(右图),第二层意义是两个人账户的状态一致(左图)。这两层含义表现完全不同,对于前者,一个账户的修改会影响另一个账户的状态,对于后者,两个账户状态则是完全独立的。

不论哪一层意义,同一的概念都复杂很多 —— 因为同一的判定现在涉及时间维度:对于在时间维度完全替换过零件的船,它还是原来那艘船吗?Java 费很大的力气去强制程序员处理 equals 就是这个原因。且不说吃力不讨好,equals 的处理一般强行选取一个时间切面对比状态,和 == 一起,用来对同一的两层含义进行判断。下面这个修改过的 bank 过程可通过 make-joint 过程允许多人通过不同密码共享同一对象,这个例子表明了,在某些情况下,环境模型中,解决复杂的同一性问题还是有价值的:
(define (bank secret account)
(define (memq? items x)
(cond ((null? items) #f)
((eq? (car items) x) #t)
(memq? (cdr items) x)))
(let ((retry 7) (sec-list (list secret)))
(define (call-the-cops)
(begin (set! retry 0) (printf "CALLING 110 NOW...\n")))
(define (store money)
(begin (set! account (+ account money)) account))
(define (take money)
(let ((rest (- account money)))
(if (< rest 0)
(begin (printf "Not enough money in your account\n") -1)
(begin (set! account rest) rest))))
(define (dispatch pass method . args)
(cond ((not (and (symbol? pass) (memq? sec-list pass)))
(begin (set! retry (- retry 1))
(if (< retry 0) (call-the-cops))
(printf "Error password, retry ~d\n" retry) -1))
((eq? method 'store) (apply store args))
((eq? method 'take) (apply take args))
((eq? method 'add-pass) (set! sec-list (cons (car args) sec-list)))
(else (error "no support method" method))))
(if (symbol? secret) dispatch (error "not a valid password" secret))))
(define (make-joint account password new-password)
(begin (account password 'add-pass new-password) account))
(define peter-acc (bank 'open-sesame 100))
(define paul-acc (make-joint peter-acc 'open-sesame 'rosebud))
(peter-acc 'open-sesame 'take 50) ;√
(paul-acc 'open-sesame 'take 70) ;Not enough money
但是并不是所有的概念都适合这么看,比如一个有理数的概念,就完全不需要看做具有标识的可修改对象,也不想让两个不同的有理数修改分子实现“同一个”有理数。总而言之,对于同一的不同理解导致了程序行为可能出现不同的变化,这种问题并不是程序设计语言的问题,而是将概念看做一个可变状态对象的结果,是环境模型的阿喀琉斯之踵。最后,在代码开发上,带有赋值的环境模型强迫我们考虑赋值的相对顺序,以保证每个语句使用的都是被修改变量的正确版本,而在函数式程序设计中,这一问题完全不存在(符号就是值,只有一份,永不可变)。而在并发环境下,考虑赋值的相对顺序将难上加难。下面这个例子展示了表达式求值顺序(从左到右 or 从右到左)不同导致的赋值顺序差异以及其对结果的影响。
(define (left-or-right?) (let ((first #t))
(lambda (value)
(if first (begin (set! first #f) value) 0))))
(define f (left-or-right?))
(printf "~s\n" (+ (f 0) (f 1))) ;0 in Chez, Gauche; 1 in MIT, Biwa
求值的环境模型
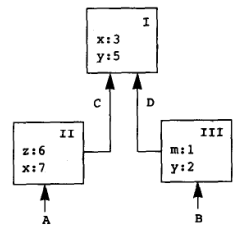
一个环境指的就是框架 frame 的一个序列,每个框架包含了一些对于变量的值关联的约束,在任一框架中,任何变量最多只能有一个约束。每个框架包含一个指针,指向其外围环境,对于没有外围环境的框架,将其看做全局框架。在右侧这个环境中包含三个框架,其中 II 和 III 的外部框架指向 I,I 是全局框架。A - D 是环境指针,在环境 A 中,x 被约束为 7(尽管在外部框架 I 中 x 被约束为 3,但 II 中的环境遮蔽了这一约束),z 被约束为 6,y 被约束为 5;在环境 B 中,m 被约束为 1,y 为 2,x 为 3。这种模型就好像投影,每层框架的约束彼此重叠,底层覆盖高层,最终形成表达式求值的上下文。
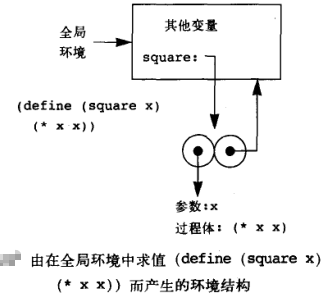
在环境模型中的求值规则和代换模型类似,包含两个步骤:①求值组合式中各个子表达式(包括操作符和操作对象);②将运算符子表达式的值应用于运算对象子表达式的值。但是,将一个复合过程应用于参数在环境模型中的含义并不相同,在环境模型中,一个过程总是一个对偶,包括代码(一个 lambda 表达式(define 直接定义看做 lambda 语法糖))和指向环境的指针,求值此表达式指的就是在全局环境中将过程名符号约束到此求值结果上去,比如 (define (square x) (* x x)) 的求值本质就是在全局环境中将 square 这一符号通过向下箭头关联到一个特定过程(这一过程本身包含指向全局环境的向上指针),为此框架加入新的约束,如下所示:
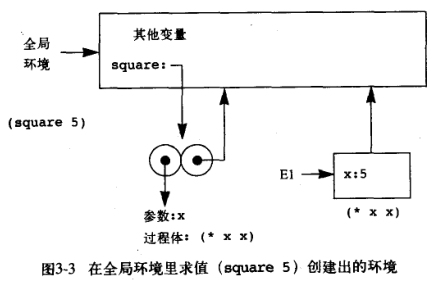
而将一个过程应用于一组实际参数,其会建立一个新的环境,后者包含将所有形式参数约束于对应的实际参数的框架,此框架外围环境就是此过程所在的环境,过程体在此新环境下进行求值。比如对 (square 5) 进行求值,这里从 square 所在的全局环境创建了环境 E1,其中形参被实参替换,进行求值得到了 25。
对于在某个环境中求值 (set!
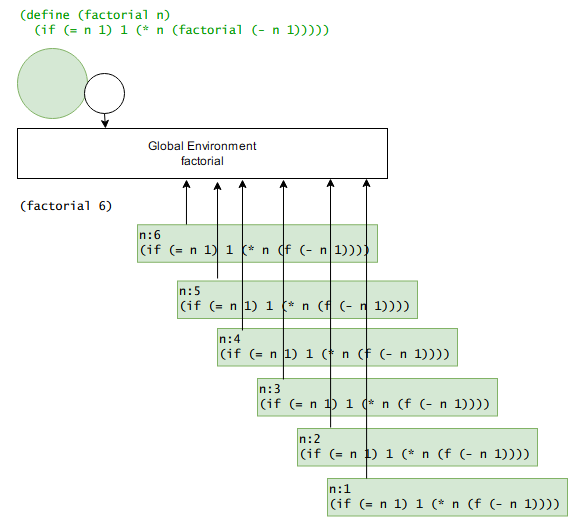
上图是递归应用 factorial 的例子,在这个例子中,先求值子表达式,factorial 绑定到全局环境的 lambda 表达式上,其应用过程为从此 factorial 指定的环境出发创建一个子环境,然后将实参 6 替换 n,进行求值。在求值的过程中又遇到了 factorial,在全局环境中找到它,因此继续创建新环境,周而复始,直到 n 为 1,在此环境下得到值 1,依次在栈中弹回得到最终的结果。
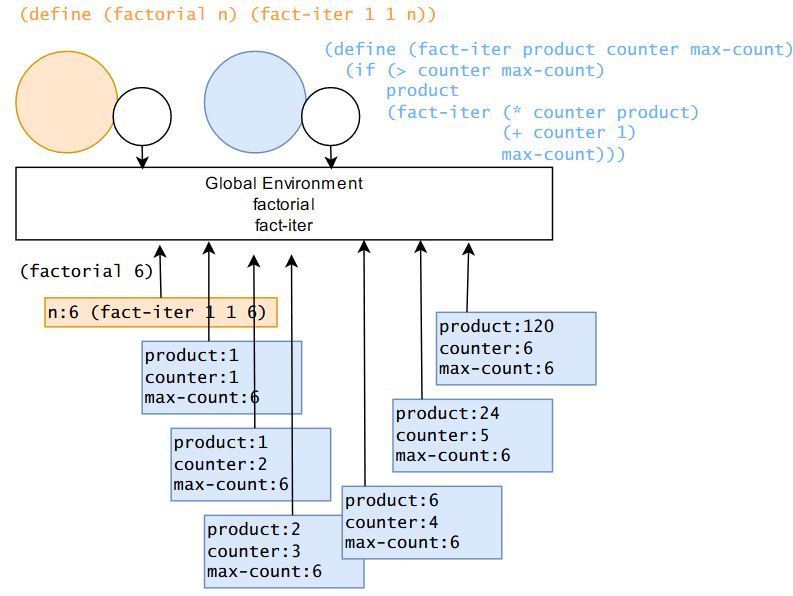
上图是迭代应用 factorial 的例子,其原理类似,先在全局环境找到 factorial,根据其指定的全局环境创建子环境(黄色),然后求值遇到 fact-iter,从全局环境中找到并创建子环境,实参替换形参进行求值,周而复始遇到 fact-iter,因此每次都创建子环境,最后得到结果 120,按照栈弹回得到 (factorial 6) 的结果。
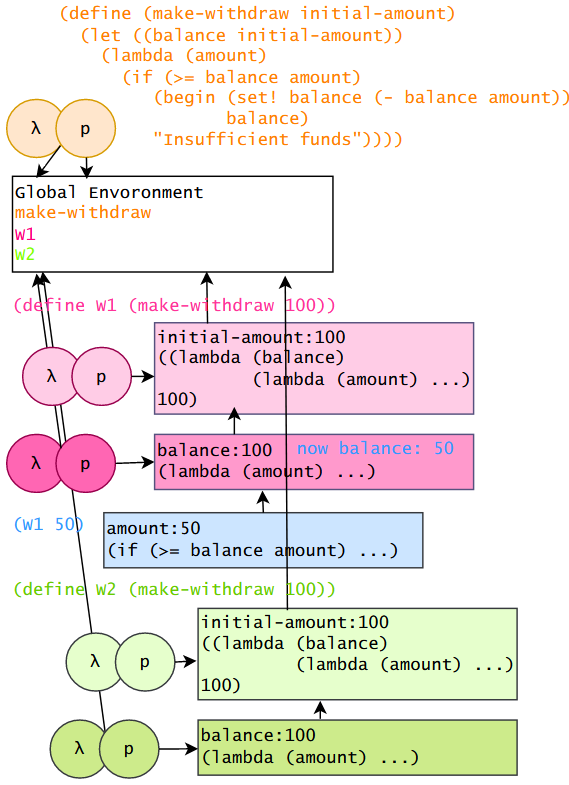
上面这个例子更为全面的展示了 define lambda 表达式的绑定以及过程应用实参的过程,以及闭包和局部赋值的本质。首先 W1 表达式会先执行 make-withdraw 过程,其从全局环境查到后,根据代码应用实参100,并根据 make-withdraw 所指全局环境创建局部环境(浅红色),let 是 lambda 语法糖,因此这里相当于对一个匿名表达式应用 100 实参,这里的匿名表达式序对(浅红色)并没有绑定到全局变量,其指针指向此子环境。对此序对求值会执行代码,子2环境(深红色)指向匿名表达式序对(浅红色)指针所指向的子1环境(浅红色),当返回后此 lambda 表达式(深红色)整体被绑定到全局环境的 W1 符号。
为 W1 传递 50 实参,会查找此序对(深红色),其左边代码形参被替换实参,基于右边指针创建子环境(蓝色),然后求值,这里 set! 修改了符号 balance,从环境的框架逐步查找此符号,在深红色框架找到后进行修改。
W2 表达式的求值、W2 符号的全局空间绑定和 W1 类似,不再赘述,注意,如果再对 W2 传递 50 实参,那么其 balance 所指的会是深绿色框架,和 W1 所在的深红色框架中的值无关。

上面这个例子展示了内部定义的实现。简而言之,局部过程用于程序模块化的核心在于:①局部过程的名字不会和包容其过程之外的名字干扰,因为其在过程运行时创建的框架中约束,而非全局环境。②局部环境只要将包含它们的过程的形参作为自由变量就可以访问此过程的实际参数,因为局部过程体的求值所在环境是外围过程求值所在的环境的下属,因此这里形参可以找到(实际上构造这些局部过程时实参已经替换了形参,所以对于形参函数体而言,其外部形参符号已经是数值了)。
就这个取款的过程而言,局部过程在绿色环境中定义,withdraw, deposit 和 dispatch 符号被绑定,当调用 (acc 'deposit) 时,基于此创建了新的环境,这里返回了 deposit 在绿色环境被找到,然后应用实参 40,这里设置 balance 变量,其存在于绿色环境中,现在被修改为 90。对于 acc2 而言,也是如此,注意这里共享的只有全局环境,而如果 (acc 'withdraw) 的时候,其共享的则是绿色环境,可以自由访问这里的其他符号和值,比如对 balance 进行操作。
用变动数据做模拟
变动的表结构
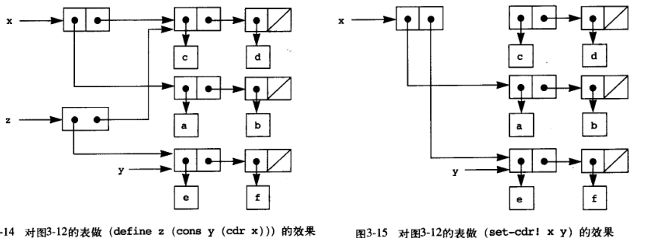
;同一与变化 当序对和表可以变动时,环境模型的优缺点就更为明显的表现了出来。相比较 cons, car 和 cdr, append,可使用 set-car!, set-cdr! 以及 append! 来就地修改表结构。这种就地修改乍一看简化了表的操作,但其实不然,如下所示,z1 通过迭代模型将 y 作为 x 序对的第一个元素,这里其实内部共享了 '(c d) 这个元素,但因为不论 x y 还是 z1 都不可修改,因此这种共享无害。而在 z2 中,就地替换的 set-cdr! 直接让 x 的后半序对被替换为 y,这里之前的 '(c d) 被垃圾回收,看起来更加简洁,但其实不然,现在的 x 被破坏了,虽然我们可能只想得到 z2 没想破坏它。
(define x '((a b) (c d)))
(define y '(e f))
(define z1 (cons y (cdr x)))
(display x) ;((a b) (c d))
(define z2 (set-cdr! x y))
(display x) ;((a b) (e f))
append! 也是如此,如下所示,本意我们只想得到一个合并了 a b 的 c,但使用 append! 会增加对 a 的副作用。这种同一性改变导致的变化使得我们不得不将符号放在操作的时间维度进行小心的判断。last-pair 此处被用来实现获取表的最后一个序对,make-cycle 利用可变的 set-cdr! 很容易实现了环,即让一个序对末尾和头部相连,造成了隐患 —— 这种隐患的本质来自于同一性改变导致的符号含义变化,使一个符号在时间维度有不同的表现。
(define a '(a b))
(define b '(c d))
(define c1 (append a b))
(display a) ;(a b)
(define c2 (append! a b))
(display a) ;(a b c d)
(define (last-pair x)
(if (null? (cdr x)) x (last-pair (cdr x))))
(define (make-cycle x)
(set-cdr! (last-pair x) x) x)
(printf "~s\n" (make-cycle '(a b c)))
在环境模型中因为同一和变化特点导致的问题有很多,大致分为以下三点(对于 Java 程序员而言,这三点是他们职业生涯开始时习以为常的不得不忍受的痛苦:值vs引用,相等性判断,状态顺序带来的心智负担):
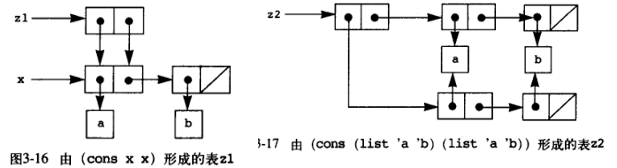
1. 共享不再简单可靠。在 Scheme 的实现中,代换模型中大量共享了指针地址,但这种共享与直接使用值构造对程序正确性没有任何影响(eq? 用来检查指针相等,但如下 e1 e2 即便不 eq? 也不影响使用,因为 e1 和 e2,包括组成 e1 的 d 不可赋值,因此安全性得以保障),而一旦使用环境模型引入可变性,这将导致共享存在严重的问题:要在任何时候注意值传递和引用传递的差别,避免因为同一与变化导致的意外共享的问题(比如 fuck 过程就导致了不同方式构造的 e 产生了差别):
(define d '(a b))
(define e1 (cons d d))
(define e2 (cons '(a b) '(a b)))
(define (fuck e) (set-car! (car e) 'fuck) e)
(printf "~s ~s\n" (fuck e1) (fuck e2))
;((fuck b) fuck b) ((fuck b) a b)
(printf "eq?~s eq?~s\n"
(eq? (car e1) (cdr e1)) ;#t for same ref
(eq? (car e2) (cdr e2))) ;#f for same value
2. 需要对相等性问题额外处理。对表的序对统计本来是一个及其简单的过程,现在因为同一和变化的问题,允许赋值导致了序对可能部分或全部成环:三个序对,count-pairs-1 可能返回 3,4,7 甚至不返回:

count-pairs-2 使用了一个 memo 列表来记录出现的序对以正确实现了序对统计:
(define (count-pairs-2 x)
(define (inner x memo)
(if (and (pair? x) (not (memq x memo)))
(inner (car x) (inner (cdr x) (cons x memo)))
memo))
(length (inner x '())))
(printf "~s\n" (count-pairs-2 (make-cycle '(1 2 3))))
因为可变表结构的这种问题,设计了 loop-detector 用于检测成环,这里 mirror 是一个任意的东西,每次从表获取 car 后将其设置为这个东西,如果成环,那么我们将在某个 car 后得到 mirror,这样就实现了环检测。
(define (loop-detector x)
(let ((id (cons '() '())))
(define (loop remains)
(cond ((null? remains) #f)
((eq? id (car remains)) #t)
(else (set-car! remains mirror)
(loop (cdr remains)))))
(loop x)))
(printf "~s ~s\n" (loop-detector '(1 2 3))
(loop-detector (make-cycle '(1 2 3))))
3.把握状态顺序的心智负担。这种同一性变化带来的最后一个大问题就是对心智的负担,哪怕是一个简单的 reverse 函数,如下函数利用 set-cdr! 实现了对表的反向。
(define (reverse-s x)
(define (loop x y)
(if (null? x) y
(let ((temp (cdr x)))
(set-cdr! x y)
(loop temp x))))
(loop x '()))
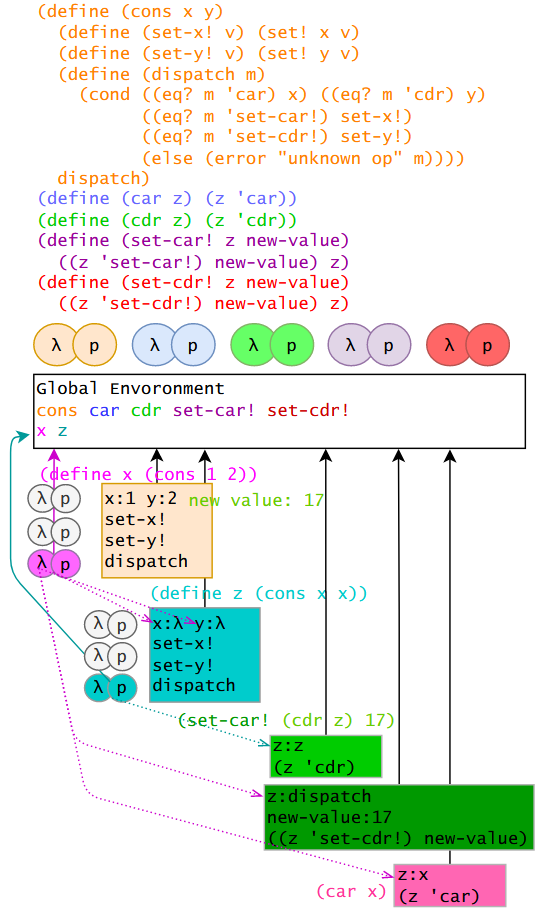
这种对表结构的改变本质就是赋值。在之前的章节中,通过过程实现了序对,而序对的变动,则可以通过对实现序对的值进行赋值来实现。左图提供了其实现代码和环境过程表示。
当 x 在全局环境绑定 (cons 1 2) 的结果时,先找到 cons 代码,然后构造子环境(橙色)并返回 dispatch 对象(粉红色)并和符号 x 进行绑定。当 z 在全局环境绑定 (cons x x) 时,同样构造子环境(青色),传入 x 绑定的值:lambda 表达式,然后返回 dispatch 对象(青色)。
调用 cdr z 以及 set-car! 过程依次创建浅绿色和深绿色环境,前者通过对青色 lambda 调用依次调用青色环境的 set-y! 返回局部值 x,即紫色 lambda,后者通过对传入的紫色 lambda 求值调用橙色环境 set-x! 修改 x 的值为 17。
而最后,调用 car x 会创建粉红色环境,实参为粉红色 lambda,执行代码会返回 y 值,即 17。
队列的表示
如果不使用队列的环境模型(即赋值和使用可变表结构),队列 FIFO 的实现会很笨拙:
(define (make-queue) '())
(define (empty-queue? q) (empty? q))
(define (front-queue q) (car q))
(define (insert-queue! q item) (append q (list item)))
(define (delete-queue! q) (cdr q))
(define q (make-queue))
(define q1 (insert-queue! q 'a))
(define q2 (insert-queue! q1 'b))
(define q3 (delete-queue! q2))
(define q4 (insert-queue! q3 'c))
(define q5 (insert-queue! q4 'd))
(define q6 (delete-queue! q5))
(printf "~s ~s ~s ~s ~s ~s\n" q1 q2 q3 q4 q5 q6)
而一旦决定引入可变表结构,队列的创建依旧不方便 —— 充满了可变指针,但使用非常简单了,尤其是引入局部变量闭包加上消息传递风格时(OOP)。这里队列的实现使用序对,队列包含一个包含头尾的管理序对,以方便从后部插入和从前部取出,这个序对关联两个数据序对,序对指针包含数据和指向下一个数据序对的指针,如下图所示:
--------
q -----> |⚪|⚪| -----------------------
-------- |
| |
-------- -------- --------
|⚪|⚪|---->|⚪|⚪|---->|⚪|⚪|
-------- -------- --------
| | |
a b c如下四个选择函数用来直接操作前后的数据序对:
(define (front-ptr q) (car q))
(define (rear-ptr q) (cdr q))
(define (set-front-ptr! q pair) (set-car! q pair))
(define (set-rear-ptr! q pair) (set-cdr! q pair))
如下的实现比较简单,获取头部元素就是获取第一个数据序对的值,插入元素就是更新尾部数据序对,使其指向新的数据序对,然后更新管理序对指向末尾的引用。删除元素就是将头部引用指向从原头部数据序对的下一个序对上。打印序对这里从头部数据序对开始不断遍历直到没有下一个元素为止。
(define (make-queue) (cons '() '()))
(define (empty-queue? q) (null? (front-ptr q)))
(define (front-queue q)
(if (empty-queue? q)
(error "empty queue call front!" q)
(car (front-ptr q))))
(define (insert-queue! q item)
(let ((new-pair (cons item '())))
(cond ((empty-queue? q)
(set-front-ptr! q new-pair)
(set-rear-ptr! q new-pair)
q)
(else
(set-cdr! (rear-ptr q) new-pair)
(set-rear-ptr! q new-pair)
q))))
(define (delete-queue! q)
(cond ((empty-queue? q)
(error "empty queue call delete!" q))
(else (set-front-ptr! q (cdr (front-ptr q))) q)))
(define (print-queue q)
(define (handle-all item)
(if (or (null? item) (not (pair? item))) (newline)
(begin (printf "~s " (car item))
(handle-all (cdr item)))))
(if (empty-queue? q) (newline)
(handle-all (front-ptr q))))
(define q (make-queue))
(print-queue (insert-queue! q 'a))
(print-queue (insert-queue! q 'b))
(print-queue (delete-queue! q))
(print-queue (insert-queue! q 'c))
(print-queue (insert-queue! q 'd))
(print-queue (delete-queue! q))
如果说环境模型简化了队列的使用,那么闭包和消息传递风格则进一步简化了队列的使用,其代码和上面几乎一致,除了每个方法不再需要传递 q 并且从 q 中通过选择函数选择头部和尾部数据序对了:
(define (make-queue)
(let ((front-ptr '())
(rear-ptr '()))
(define (empty-queue?) (null? front-ptr))
(define (front-queue)
(if (empty-queue?)
(error "empty queue call front!")
(car front-ptr)))
(define (insert-queue! item)
(let ((new-pair (cons item '())))
(cond ((empty-queue?)
(set! front-ptr new-pair)
(set! rear-ptr new-pair))
(else
(set-cdr! rear-ptr new-pair)
(set! rear-ptr new-pair)))))
(define (delete-queue!)
(cond ((empty-queue?) (error "empty queue call delete!" -1))
(else (set! front-ptr (cdr front-ptr)))))
(define (print-queue)
(define (handle-all item)
(if (or (null? item) (not (pair? item))) (newline)
(begin (printf "~s " (car item))
(handle-all (cdr item)))))
(if (empty-queue?) (newline)
(handle-all front-ptr)))
(define (dispatch m . args)
(cond ((eq? m 'empty-queue?) (empty-queue))
((eq? m 'front-queue) (front-queue))
((eq? m 'insert-queue!) (insert-queue! (car args)))
((eq? m 'delete-queue!) (delete-queue!))
((eq? m 'print-queue) (print-queue))))
dispatch))
(define q (make-queue))
(q 'insert-queue! 'a)
(q 'print-queue)
(q 'insert-queue! 'b)
(q 'print-queue)
(q 'delete-queue!)
(q 'print-queue)
(q 'insert-queue! 'c)
(q 'print-queue)
(q 'insert-queue! 'd)
(q 'print-queue)
(q 'delete-queue!)
(q 'print-queue)
最后,还有一种队列称之为双端队列,其实现的数据结构和单端队列大致相同,如果不追求从双端队列末尾删除元素的 Θ(1) 时间效率的话 —— 因为从末尾删除后,需要更新倒数第二个数据序对指向末尾指针,现有数据结构做不到这一点。为此,需要维护双向指针,其数据结构大致如下所示(第三排的两个指针分别指向前后第二排的数据序对,称其为导航序对):
--------
q -----> |⚪|⚪| ---------------------
-------- |
| |
-------- -------- --------
|⚪|⚪| |⚪|⚪| |⚪|⚪|
-------- -------- --------
| | | | | |
a | b | c |
-------- -------- --------
|⚪|⚪|<---->|⚪|⚪|<--->|⚪|⚪|
-------- -------- --------基于这样的数据结构,实现非常复杂,充斥着指针操作。这里 make-deque 和 empty-deque? 和 front-deque, rear-deque 都很简单,和之前代码一致,但 front-insert-deque! 就比较复杂,其涉及先获取现有头部数据序对,然后依赖此指针构造新的数据序对 + 导航序对,并且更新旧的数据序对中的导航序对,使其反向指向此新数据序对,然后将新的数据序对插入头部管理序对。rear-insert-deque! 类似,先获取旧的数据序对以构造新的数据序对 + 导航序对,然后更新旧的数据序对的导航序对指向新的数据序对,然后将指向末尾的管理序对指向新的数据序对。
(define (make-deque) (cons '() '())) ;构造空双端队列
(define (empty-deque? q) (null? (front-ptr q))) ;判断双端队列是否为空
(define (front-deque q) ;第一个元素
(if (empty-deque? q)
(error "empty deque call front!" q)
(car (front-ptr q))))
(define (rear-deque q) ;最后一个元素
(if (empty-deque? q)
(error "empty deque call rear!" q)
(car (rear-ptr q))))
(define (front-insert-deque! q item) ;从前插入一个元素
(if (empty-deque? q)
(let ((new-pair (cons item (cons '() '()))))
(set-front-ptr! q new-pair)
(set-rear-ptr! q new-pair) q)
(let ((new-pair (cons item (cons '() (front-ptr q)))))
(set-car! (cdr (front-ptr q)) new-pair)
(set-front-ptr! q new-pair) q)))
(define (rear-insert-deque! q item) ;从后插入一个元素
(if (empty-deque? q)
(let ((new-pair (cons item (cons '() '()))))
(set-front-ptr! q new-pair)
(set-rear-ptr! q new-pair) q)
(let ((new-pair (cons item (cons (rear-ptr q) '()))))
(set-cdr! (cdr (rear-ptr q)) new-pair)
(set-rear-ptr! q new-pair) q)))
删除现在比插入更复杂:front-delete-deque! 从头部删除,先获取需要删除的数据序对,根据此序对的导航序对获取新的数据序对,然后将彼此的导航序对引用解除,将指向头部的管理序对指向新的数据序对。rear-delete-deque! 从尾部删除,同样先获取旧的和新的数据序对,彼此解除导航序对的关联以方便垃圾回收,然后更新指向尾部的管理序对指向新的末尾数据序对。打印 print-deque 代码略微进行了修改,隐藏了导航序对的信息,只依赖导航序对链条仅显示链条上的数据序对。
(define (front-delete-deque! q) ;从头端删除
(cond ((empty-deque? q)
(error "empty queue call delete!" q))
(else
(let ((old-pair (front-ptr q))
(new-pair (cddr (front-ptr q))))
(set-cdr! (cdr old-pair) '())
(set-car! (cdr new-pair) '())
(set-front-ptr! q new-pair) q))))
(define (rear-delete-deque! q) ;从末端删除
(cond ((empty-deque? q)
(error "empty queue call delete!" q))
(else (let ((old-pair (rear-ptr q))
(new-pair (cadr (rear-ptr q))))
(set-cdr! (cdr new-pair) '())
(set-car! (cdr old-pair) '())
(set-rear-ptr! q new-pair)) q)))
(define (print-deque q)
(define (handle-all item)
(if (or (null? item) (not (pair? item))) (newline)
(begin (printf "~s " (car item))
(handle-all (cddr item)))))
(if (empty-deque? q) (newline)
(handle-all (front-ptr q))))
(define q (make-deque))
(print-deque (front-insert-deque! q 'a))
(print-deque (front-insert-deque! q 'b))
(print-deque (front-delete-deque! q))
(print-deque (rear-insert-deque! q 'c))
(print-deque (rear-insert-deque! q 'd))
(print-deque (rear-delete-deque! q))
表格的表示
表格指的是能够表示一个 key 和一个 value 关联的数据结构。下面提供了一种简单的实现:
table
|
-------- -------- -------- --------
|⚪|⚪| ----->|⚪|⚪|-----> |⚪|⚪|------>|⚪|⚪|
-------- -------- -------- --------
| | | |
*table* -------- -------- --------
|⚪|⚪| |⚪|⚪| |⚪|⚪|
-------- -------- --------
| | | | | |
a 1 b 2 c 3(define (lookup key table)
;查找表格,返回匹配的 key 对应的 value,找不到返回 #f
(let ((record (assoc key (cdr table))))
(if record (cdr record) #f)))
(define (assoc key records)
;在导航序对中查找 key, 返回匹配的数据序对
(cond ((null? records) #f)
((equal? key (caar records)) (car records))
(else (assoc key (cdr records)))))
(define (insert! key value table)
;插入元素,如果存在则替换,不存在则插入 table 头部
(let ((record (assoc key (cdr table))))
(if record (set-cdr! record value)
(set-cdr! table (cons (cons key value)
(cdr table))))))
(define (make-table) (list '*table*))
下面的数据结构提供了二维表格(可变长度)的实现,其代码采用了 CPS 风格,节省了对选择函数的调用。注意,这里每个第一维 key 选择后,得到的结果是一个完全等价于第一维表格的子表格,要获取其导航序对需要 cdr 才可以(这种选择只是为了美观,实际并不必须,在下面的 n 维表格实现中为了实现简单就避免了这个不必要的 cons)。
-------- -------- -------- --------
|⚪|⚪| ----->|⚪|⚪|-----> |⚪|⚪|------>|⚪|⚪|
-------- -------- -------- --------
| | | |
*table* -------- -------- --------
|⚪|⚪| |⚪|⚪| |⚪|⚪|
-------- -------- --------
| | | | | |
a | b 2 c 3
-------- -------- -------- --------
|⚪|⚪| ----->|⚪|⚪|-----> |⚪|⚪|------>|⚪|⚪|
-------- -------- -------- --------
| | | |
*table* -------- -------- --------
|⚪|⚪| |⚪|⚪| |⚪|⚪|
-------- -------- --------
| | | | | |
+ 1 - 2 * 3 (define (make-table-2 same-key?)
(let ((local-table (list '*table*)))
(define (assoc key records)
;在导航序对中查找 key, 返回匹配的数据序对
(cond ((null? records) #f)
((same-key? key (caar records)) (car records))
(else (assoc key (cdr records)))))
(define (lookup key-1 key-2)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record (cdr record) #f))
#f)))
(define (insert! key-1 key-2 value)
(let ((subtable (assoc key-1 (cdr local-table))))
(if subtable
(let ((record (assoc key-2 (cdr subtable))))
(if record
(set-cdr! record value)
(set-cdr! subtable
(cons (cons key-2 value)
(cdr subtable)))))
(set-cdr! local-table
(cons (list key-1
(cons key-2 value))
(cdr local-table)))))
'ok)
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "unknown op" m))))
dispatch))
(define t1 (make-table-2 equal?))
(define get (t1 'lookup-proc))
(define put (t1 'insert-proc!))
(put 'A 'a 23)
(display (get 'A 'a))
下面提供了多维表格的实现,和二维类似又不尽相同,这里为了实现简单除了第一维外子表格直接挂在父表格数据序对的 cdr 上,多维的插入比较复杂,涉及路径存在和不存在的问题,如果路径存在且数据存在,直接替换,如果路径存在但数据不存在,则向此维度子表格插入数据到头部,并更新父维度数据序对 cdr。如果路径不存在,则递归创建此维度 —— 依赖子维度返回的子维度数据结构。
table
-------- -------- -------- --------
|⚪|⚪| ----->|⚪|⚪|-----> |⚪|⚪|------>|⚪|⚪|
-------- -------- -------- --------
| | | |
*table* -------- -------- --------
|⚪|⚪| |⚪|⚪| |⚪|⚪|
-------- -------- --------
| | | | | |
a | b 2 c 3
-------- -------- --------
|⚪|⚪|-----> |⚪|⚪|------>|⚪|⚪|
-------- -------- --------
| | |
-------- -------- --------
|⚪|⚪| |⚪|⚪| |⚪|⚪|
-------- -------- --------
| | | | | |
+ 1 - 2 * 3 (define (make-table-n same-key?) (let ((local-table (list '*table*)))
(define (assoc key records)
(cond ((null? records) #f)
((same-key? key (caar records)) (car records))
(else (assoc key (cdr records)))))
(define (lookup . keys)
(define (lookup-inner table-now keys)
(if (null? keys) #f
(let ((key-now (car keys)))
(let ((subtable (assoc key-now (cdr table-now))))
(if (not subtable) #f
(if (not (null? (cdr keys)))
(lookup-inner subtable (cdr keys))
(cdr subtable)))))))
(lookup-inner local-table keys))
(define (insert! value . keys)
(define (insert-inner table-now keys)
(if (null? keys) #f
(let ((key-now (car keys)))
(let ((subtable (assoc key-now (cdr table-now))))
(cond ((and subtable (not (null? (cdr keys))))
;尚未遍历完毕整条路径,但存在此节点,继续递归
(insert-inner subtable (cdr keys))
table-now)
((and (not subtable) (not (null? (cdr keys))))
;尚未遍历完毕整条路径,且不存在此节点
(set-cdr! table-now
(cons
(let ((this-node (insert-inner (cons '() '()) (cdr keys))))
(set-car! this-node key-now) this-node)
(cdr table-now)))
table-now)
((and subtable (null? (cdr keys)))
;整条路径遍历完毕且存在当前值
(set-cdr! subtable value)
table-now)
((and (not subtable) (null? (cdr keys)))
;整条路径遍历完毕且不存在当前值
(set-cdr! table-now (cons (cons key-now value) (cdr table-now)))
table-now)
(else (error "not a option here" 233)))))))
(insert-inner local-table keys))
(define (dispatch m)
(cond ((eq? m 'lookup-proc) lookup)
((eq? m 'insert-proc!) insert!)
(else (error "unknown op" m))))
dispatch))
(define t1 (make-table-n equal?))
(define get (t1 'lookup-proc))
(define put (t1 'insert-proc!))
(put 23 'A 'a)
(put 24 'A 'b)
(put 25 'B 'c)
(put 26 'D 'e '+)
(display (get 'A 'a))
(display (get 'A 'b))
(display (get 'B 'c))
(display (get 'D 'e '-))
最后,这三种实现都是“无序”表格,查找效率较差,可以基于二叉树 tree 的数据抽象实现更高效的表格(一维),在查询频繁的场景下效率较高:
(define (make-table compare)
(define (make-tree key value left-branch right-branch)
(list key value left-branch right-branch))
(define (tree-key tree) (car tree))
(define (tree-value tree) (cadr tree))
(define (tree-left-branch tree) (caddr tree))
(define (tree-right-branch tree) (cadddr tree))
(define (tree-empty? tree) (null? tree))
(define (tree-set-key! new-key tree)
(set-car! tree new-key))
(define (tree-set-value! new-value tree)
(set-car! (cdr tree) new-value))
(define (tree-set-left-branch! new-left-branch tree)
(set-car! (cddr tree) new-left-branch))
(define (tree-set-right-branch! new-right-branch tree)
(set-car! (cdddr tree) new-right-branch))
(define (tree-insert! tree given-key value compare)
(if (tree-empty? tree) (make-tree given-key value '() '())
(let ((compare-result (compare given-key (tree-key tree))))
(cond ((= 0 compare-result) (tree-set-value! value tree) tree)
((= 1 compare-result)
(tree-set-right-branch!
(tree-insert! (tree-right-branch tree) given-key value compare)
tree) tree)
((= -1 compare-result)
(tree-set-left-branch!
(tree-insert! (tree-left-branch tree) given-key value compare)
tree) tree)))))
(define (tree-search tree given-key compare)
(if (tree-empty? tree) '()
(let ((compare-result (compare given-key (tree-key tree))))
(cond ((= 0 compare-result) tree)
((= 1 compare-result)
(tree-search (tree-right-branch tree) given-key compare))
((= -1 compare-result)
(tree-search (tree-left-branch tree) given-key compare))))))
(let ((t '()))
(define (empty?) (tree-empty? t))
(define (insert! given-key value)
(set! t (tree-insert! t given-key value compare)) 'ok)
(define (lookup given-key)
(let ((result (tree-search t given-key compare)))
(if (null? result) #f
(tree-value result))))
(define (dispatch m)
(cond ((eq? m 'insert!) insert!)
((eq? m 'lookup) lookup)
((eq? m 'empty?) (empty?))
(else (error "Unknow mode " m))))
dispatch))
(define (compare-string x y)
(cond ((string=? x y) 0)
((string>? x y) 1)
((string<? x y) -1)))
(define (compare-symbol x y)
(compare-string (symbol->string x) (symbol->string y)))
(define (compare-number x y)
(cond ((= x y) 0) ((> x y) 1) ((< x y) -1)))
(define t1 (make-table compare-symbol))
(define insert (t1 'insert!))
(define lookup (t1 'lookup))
(insert 'a 23) (insert 'b '24)
(display (lookup 'b))
下面提供了基于表格的一种用途:作为计算缓存。注意 memo-fib 可将递归的 fib 过程时间消耗控制在 θ(n) 级别,注意这里不能简单是 (memoize fib),因为后者会在 fib 过程中调用 fib 而非 memoize 包装的 fib,即缓存不会被调用:
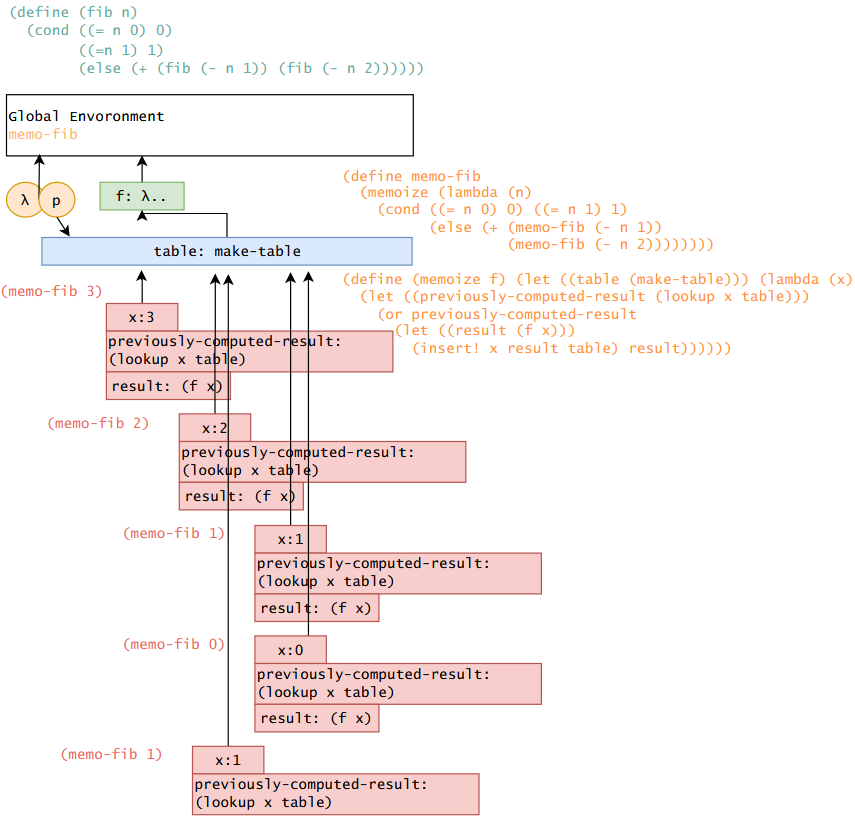
上面这个表简单的画出了 (memo-fib 3) 的环境图,table 在这里作为缓存中心,调用 f 3 的时候,其调用了 f 2,f 2 又递归调用了 f 1 和 f 0,最后栈回到 f 2 后,调用 f 1 时直接从缓存中找到就返回了,虽然在这个例子中 f 1 简单的等于 1,但是这反映了缓存的理念,当 n 越大,缓存的效果越好。
数字电路的模拟器
下面的实例通过事件回调风格实现了数字电路的模拟,这里的数字电路通过与、或、非门进行组合,构成了半加器、全加器以及加法运算器。
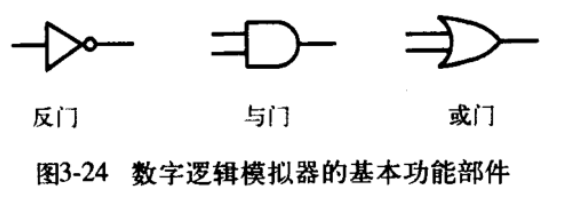
为了完成数字电路的模拟,这里定义了几个层次的数据抽象:线路被用来承载信号(包括 0 和 1),可对线路上的信号进行读写,当线路信号值改变时触发回调函数执行动作。
(get-signal
基于线路的抽象,我们可以构建反门、与门和或门的抽象(本质就是当线路输入发生改变,输出在一定时间后根据门类进行变化),这里做的就是从输入端线路获取信号,然后设置一定延时后执行动作(对于与门和或门,执行动作的事件安装在输入线路上,但执行的动作 —— 设置信号则是操纵输出线路的信号,这是因为它们有两个输入,任一变化都会导致输出线路变化,因此要分别安装操纵输出线路的事件)。
(define (logical-not s) (if (= s 0) 1 0))
(define (inverter input output)
(define (invert-input)
(let ((new-value (logical-not (get-signal input))))
(after-delay inverter-delay
(lambda () (set-signal! output new-value)))))
(add-action! input invert-input) 'ok)
(define (logical-and s1 s2) (if (or (= s1 0) (= s2 0)) 0 1))
(define (and-gate a1 a2 output)
(define (and-action-procedure)
(let ((new-value (logical-and (get-signal a1)
(get-signal a2))))
(after-delay and-gate-delay
(lambda () (set-signal! output new-value)))))
(add-action! a1 and-action-procedure)
(add-action! a2 and-action-procedure 'ok)
(define (logical-or s1 s2) (if (or (= s1 1) (= s2 1)) 1 0))
(define (or-gate a1 a2 output)
(define (or-action-procedure)
(let ((new-value (logical-or (get-signal a1)
(get-signal a2))))
(after-delay and-gate-delay
(lambda () (set-signal! output new-value)))))
(add-action! a1 or-action-procedure)
(add-action! a2 or-action-procedure) 'ok)
注意这里的或门其实可以用非和与门合并构建起来,两个输入端都反向,然后传入与门,结果再反向即可,不过效率较低(有三倍延迟)。
接下来基于与或非门构建半加器和全加器,这里本质就是将多根电线通过这些门类相连:
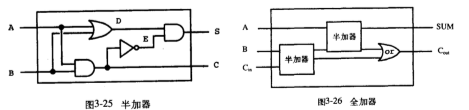
(define (half-adder a b s c)
(let ((d (make-wire)) (e (make-wire)))
(or-gate a b d)
(and-gate a b c)
(inverter c e)
(and-gate d e s) 'ok))
(define (full-adder a b c-in sum c-out)
(let ((s (make-wire))
(c1 (make-wire))
(c2 (make-wire)))
(half-adder b c-in s c1)
(half-adder a s sum c2)
(or-gate c1 c2 c-out) 'ok))
下面的 n 位的逐位进位加法器,输入的两个数二进制分别从 A 和 B 输入,An 表示第一个数的第 n 个二进制位。C 为进位表示,计算的结果放在 S 中。ripple-carry-adder 和 r 提供了加法器的两种实现,第一种好一点,代码更加清晰。
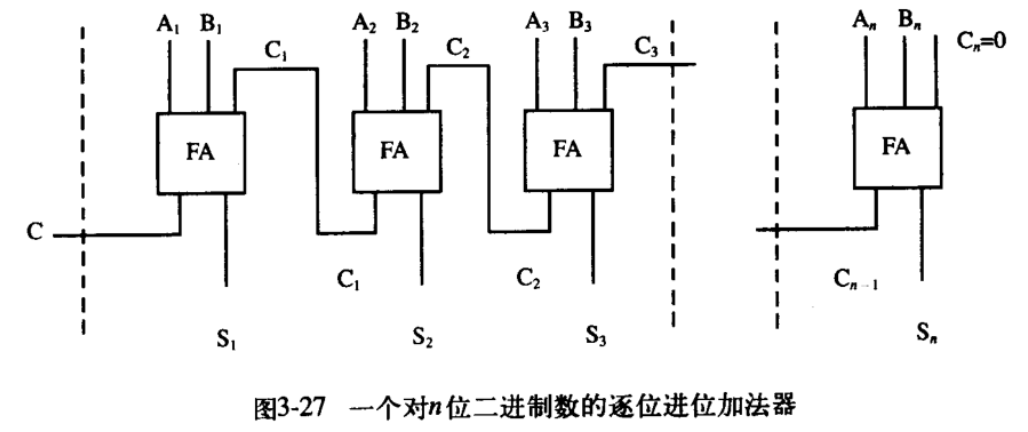
(define (ripple-carry-adder as bs ss c)
(cond ((null? as) (set-signal! c 0) c)
(else (full-adder
(car as) (car bs)
(ripple-carry-adder
(cdr as) (cdr bs) (cdr ss) (make-wire))
(car ss) c) c)))
(define (r as bs ss c)
(define (i as bs ss cs)
(if (null? as)
(let ((cc (make-wire)))
(set-signal! cc 0) cc)
(full-adder
(car as) (car bs)
(i (cdr as) (cdr bs) (cdr ss) '())
(cdr s) (if (null? cs) (make-wire) (car cs)))))
(i as bs ss (list c)))
现在我们搭建好了基于“wire”这一事件模拟回调支持的数据抽象之上的各个模块和组件,顺利实现了一个加法器,那么接下来就要考虑如何实现电线这一抽象,为了支持事件回调,这里通过封装两个内部状态来实现:signal-value 保存当前电线的值,action-procedures 存储此电线状态改变所要执行的所有事件回调。这里 CPS 风格的 get-signal 用来支持获取信号,set-signal 用来设置信号,同时出发所有回调函数,而 add-action! 则触发此事件(这里之所以立即触发是因为如果不这样,那么只有等到下一次 set-signal! 时才会被触发,这显然和 add-action! 的语义不符)并添加回调到列表。
(define (make-wire)
(let ((signal-value 0) (action-procedures '()))
(define (set-my-signal! new-value)
(if (not (= signal-value new-value))
(begin (set! signal-value new-value)
(call-each action-procedures))
'done))
(define (accept-action-procedure! proc)
(set! action-procedures (cons proc action-procedures))
(proc))
(define (dispatch m)
(cond ((eq? m 'get-signal) signal-value)
((eq? m 'set-signal!) set-my-signal!)
((eq? m 'add-action!) accept-action-procedure!)
(else (error "unknown op" m))))
dispatch))
(define (call-each procedures)
(if (null? procedures) 'done
(begin ((car procedures))
(call-each (cdr procedures)))))
(define (get-signal wire) (wire 'get-signal))
(define (set-signal! wire new-value) ((wire 'set-signal!) new-value))
(define (add-action! wire action-procedure)
((wire 'add-action!) action-procedure))
这还不算完,为了支持对上述行为的模拟,还需要实现 after-delay,即实现一个“虚拟世界”,这个世界按照时间记录了所发生的的一切。首先,这里用到了之前基于序对实现的队列,其构造和选择函数如下所示:
;队列数据结构的实现
(define (front-ptr q) (car q))
(define (rear-ptr q) (cdr q))
(define (set-front-ptr! q pair) (set-car! q pair))
(define (set-rear-ptr! q pair) (set-cdr! q pair))
(define (make-queue) (cons '() '()))
(define (empty-queue? q) (null? (front-ptr q)))
(define (front-queue q)
(if (empty-queue? q)
(error "empty queue call front!" q)
(car (front-ptr q))))
(define (insert-queue! q item)
(let ((new-pair (cons item '())))
(cond ((empty-queue? q)
(set-front-ptr! q new-pair)
(set-rear-ptr! q new-pair)
q)
(else
(set-cdr! (rear-ptr q) new-pair)
(set-rear-ptr! q new-pair)
q))))
(define (delete-queue! q)
(cond ((empty-queue? q)
(error "empty queue call delete!" q))
(else (set-front-ptr! q (cdr (front-ptr q))) q)))
(define (print-queue q)
(define (handle-all item)
(if (or (null? item) (not (pair? item))) (newline)
(begin (printf "~s " (car item))
(handle-all (cdr item)))))
(if (empty-queue? q) (newline)
(handle-all (front-ptr q))))
我们考虑将整个模拟世界通过一个叫做“待处理表”的数据抽象进行实现,其包含一些函数:判断是否为空,获取第一个、下一个、删除第一个项目、添加动作到此表,返回当前模拟时间:

这里的实现如下所示,待处理表本质就是一个当前时间 - 序列组序对,序列组包含着多个按照时间排列的序列,每个序列都是时间 - 队列序对,每个队列包含了一个或多个发生在这一时刻的事件。
;待处理表数据结构的实现
;每条时间序列结构 segment:时间 time - 队列 queue
(define (make-time-segment time queue) (cons time queue))
(define (segment-time s) (car s))
(define (segment-queue s) (cdr s))
;待处理表数据结构:当前时间 current-time - 时间序列组 segments
(define (make-agenda) (list 0))
(define (current-time a) (car a))
(define (set-current-time! a time) (set-car! a time))
(define (segments a) (cdr a))
(define (set-segments! a ss) (set-cdr! a ss))
(define (first-segment a) (car (segments a)))
(define (rest-segment a) (cdr (segments a)))
(define (empty-agenda? a) (null? (segments a)))
添加一个动作到待处理表本质就是将其插入序列组特定时间的序列的队列中,这里比较复杂的原因是,插入的时间可能和待处理表当前的时间不一致,如果其发生较晚,则直接插入,反之则需要在待处理表的序列组中找到合适的序列并插入其队列或找到合适的空隙创建序列并插入新创建的队列:
;添加到待处理表
(define (add-to-agenda! time action agenda)
;序列组为空或序列组首个序列时间早于当前时间
(define (belongs-before? segments)
(or (null? segments)
(< time (segment-time (car segments)))))
;将动作包装为 queue 并构造时间序列
(define (make-new-time-segment time action)
(let ((q (make-queue)))
(insert-queue! q action)
(make-time-segment time q)))
;此方法用于将动作插入序列组特定时间序列,其实现如下:
;从序列组头部开始,如果时间匹配则插入动作到此序列队列
;反之,对序列组其他序列逐个处理,如果现在头部序列时间更早,说明
;无时间序列匹配,构造新时间序列并将此动作插入新队列,反之继续这一过程。
(define (add-to-segments! segments)
(if (= (segment-time (car segments)) time)
(insert-queue! (segment-queue (car segments)) action)
(let ((rest (cdr segments)))
(if (belongs-before? rest)
(set-cdr! segments
(cons (make-new-time-segment time action)
(cdr segments)))
(add-to-segments! rest)))))
;对于当前待处理表的序列组,如果组第一个序列时间比当前早,即当前时间序列为空,
;那么将此动作装入新的序列并插入序列组头部。反之,调用 add-to-segments!处理。
(let ((segments (segments agenda)))
(if (belongs-before? segments)
(set-segments! agenda
(cons (make-new-time-segment time action) segments))
(add-to-segments! segments))))
获取最新时间序列的队列的第一项比较简单,注意获取后将系统时间修改为此队列时间。删除最新时间的第一项也比较简单,注意如果时间序列的队列为空,则将时间序列全部删除。
;获取最新时间的第一项
(define (first-agenda-item a)
(if (empty-agenda? a) (error "agenda empty!" 233)
(let ((first-seg (first-segment a)))
(set-current-time! a (segment-time first-seg))
(front-queue (segment-queue first-seg)))))
;删除最新时间的第一项
(define (remove-first-agenda-item! a)
(let ((q (segment-queue (first-segment a))))
(delete-queue! q)
(if (empty-queue? q) (set-segments! a (rest-segment a)))))
基于待处理表的数据抽象,我们就可以进行模拟了,创建一个“虚拟世界” the-agenda,然后定义 after-delay 就是在一定时间后往待处理表中插入一个条目,propagate 用来对待处理表的所有动作进行调用实现模拟,probe 用于获取特定线路当前的数据以及其在模拟世界的信息。
;延迟执行本质就是往待处理表中插入一条特定时间数据
(define the-agenda (make-agenda))
(define (after-delay delay action)
(add-to-agenda! (+ delay (current-time the-agenda))
action the-agenda))
;模拟本质就是对所有待处理表项目调用直到表空
(define (propagate)
(if (empty-agenda? the-agenda) 'done
(let ((first-item (first-agenda-item the-agenda)))
(first-item)
(remove-first-agenda-item! the-agenda)
(propagate))))
;获取特定线路当前状态
(define (probe name wire)
(add-action! wire (lambda ()
(printf "\n~s ~s New-value = ~s"
name (current-time the-agenda)
(get-signal wire)))))
(define inverter-delay 2)
(define and-gate-delay 3)
(define or-gate-delay 5)
接下来,构造几根电线,执行加法器过程,其会向 the-agenda 虚拟世界注册 action,调用 propagate 开始模拟,就能看到各个输出结果的电线状态,这就完成了加法的计算,比如下面的例子展示了计算 3 + 1 = 4 的整个模拟过程。
(define a1 (make-wire)) (ripple-carry-adder (list a1 a2 a3)
(define a2 (make-wire)) (list b1 b2 b3)
(define a3 (make-wire)) (list s1 s2 s3) c)
(define b1 (make-wire)) (set-signal! a1 0)
(define b2 (make-wire)) (set-signal! a2 1)
(define b3 (make-wire)) (set-signal! a3 1) ;3
(define s1 (make-wire)) (set-signal! b1 0)
(define s2 (make-wire)) (set-signal! b2 0)
(define s3 (make-wire)) (set-signal! b3 1) ;1
(define c (make-wire)) (propagate)
(probe 'result-1 s1) ;1
(probe 'result-2 s2) ;0
(probe 'result-3 s3) ;0
这个例子主要想说明的是,在 agenda 和 wire 的数据抽象与与或非门、半加器全加器以及加法器的过程抽象中,使用变动数据完成抽象封装是完全没有问题的,这和代换模型中的抽象没有任何区别。在这些特殊场景 —— 比如事件回调风格的模拟中,环境模型和变动数据能够更加灵活和贴切对客体进行抽象,符合我们的心智模型。
约束的传播
计算机是一个单向的输入输出系统,在某些情况下并不方便。在这一节将定义一种约束系统,使得连接到此系统的对象(称之为连接器)在值改变的时候,能够操纵其他连接器使得约束网络始终满足约束需求(当然,仅在一个未知条件下才可以,如果约束 a + b = 2,那么设置连接器 a 为 1,则 b 会被灌装为 2,但是如果 b 提前有值 2,那么设置 a 将导致一个冲突,必须手动清除连接器 b 的值才可以)。
下面是对 9C = 5(F - 32) 的华氏温度和摄氏温度转换的用例,为了打造这个约束系统,这里定义 make-connector 以构造连接器,在 c-f-converter 中通过 multiplier, adder, constrant 等约束条件将多个连接器约束起来,set-value! 和 forget-value! 分别对连接器设置值和删除值。
(define C (make-connector))
(define F (make-connector))
#| ___________ ____________ __________
c ----| | | |----- v ------| |
| |--- u ---| | | |-- F
w(9)--|_________| |__________|--x(5) y(32)--|________|
|#
(define (celsius-fahrenheit-converter c f)
;9C=5(F-32) 的约束
(let ((u (make-connector)) ;约束 w(9) * c = v * x(5)
(v (make-connector)) ;约束 v + y(32) = f
(w (make-connector)) ;约束 9
(x (make-connector)) ;约束 5
(y (make-connector)));约束 32
(multiplier c w u)
(multiplier v x u)
(adder v y f)
(constrant 9 w)
(constrant 5 x)
(constrant 32 y) 'ok))
(celsius-fahrenheit-converter C F)
(probe "Celsius temp" C)
(probe "Fahrenheit temp" F)
(set-value! C 25 'user)
(set-value! F 212 'user)
(forget-value! C 'user)
(set-value! F 212 'user)
采用自顶向下的方法,假如我们有了连接器的构造和选择函数 make-connector, set-value!, forget-value, connect(为此连接器加入新的约束条件),那么如何构造约束条件呢?下面提供了一些例子,简而言之,约束条件本质就是一个为连接器设置约束条件后返回的闭包,其通过 'I-have-a-value 调用闭包以根据当前连接器的值操纵可操纵的其他连接器的值来建立约束,通过 'I-lost-my-value 调用闭包以清空所有值。
; 对连接器的约束:adder, multiplier, constrant, probe
(define (adder a1 a2 sum)
(define (process-new-value)
(cond ((and (has-value? a1) (has-value? a2))
(set-value! sum (+ (get-value a1) (get-value a2)) me))
((and (has-value? a1) (has-value? sum))
(set-value! a2 (- (get-value sum) (get-value a1)) me))
((and (has-value? a2) (has-value? sum))
(set-value! a1 (- (get-value sum) (get-value a2)) me))))
(define (process-forget-value)
(forget-value! sum me)
(forget-value! a1 me)
(forget-value! a2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else (error "Unknown request" request))))
(connect a1 me)
(connect a2 me)
(connect sum me)
me)
(define (multiplier m1 m2 product)
(define (process-new-value)
(cond ((or (and (has-value? m1) (= (get-value m1) 0))
(and (has-value? m2) (= (get-value m2) 0)))
(set-value! product 0 me))
((and (has-value? m1) (has-value? m2))
(set-value! product
(* (get-value m1) (get-value m2))
me))
((and (has-value? product) (has-value? m1))
(set-value! m2
(/ (get-value product) (get-value m1))
me))
((and (has-value? product) (has-value? m2))
(set-value! m1
(/ (get-value product) (get-value m2))
me))))
(define (process-forget-value)
(forget-value! product me)
(forget-value! m1 me)
(forget-value! m2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else (error "Unknown request " request))))
(connect m1 me)
(connect m2 me)
(connect product me)
me)
(define (averager m1 m2 avg)
(define (process-new-value)
(cond ((and (has-value? m1) (has-value? m2))
(set-value! avg
(/ (+ (get-value m1) (get-value m2)) 2)
me))
((and (has-value? avg) (has-value? m1))
(set-value! m2
(- (* 2 (get-value avg)) (get-value m1))
me))
((and (has-value? avg) (has-value? m2))
(set-value! m1
(- (* 2 (get-value avg)) (get-value m2))
me))))
(define (process-forget-value)
(forget-value! product me)
(forget-value! m1 me)
(forget-value! m2 me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else (error "Unknown request " request))))
(connect m1 me)
(connect m2 me)
(connect avg me)
me)
求平均值的第二种约束条件时通过 adder, multiplier 和 constrant 实现,相当于先求和,再满足 * 0.5 等于平均值的约束。
(define (averager-2 a b c)
(let ((sum (make-connector)))
(d (make-connector))
(adder a b sum)
(multiplier sum d c)
(constrant (/ 1 2) d) 'ok))
(define (squarer a b)
(define (process-new-value)
(if (has-value? b)
(if (< (get-value b) 0)
(error "square less than 0" (get-value b))
(set-value! a (sqrt (get-value b)) me))
(if (has-value? a)
(set-value! b (square (get-value a)) me))))
(define (process-forget-value)
(forget-value! a me)
(forget-value! b me)
(process-new-value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(process-new-value))
((eq? request 'I-lost-my-value)
(process-forget-value))
(else (error "Unknown request " request))))
(connect a me)
(connect b me)
me)
注意,求平方不能用这个 squarer-x 过程,因为 a 可以推 b,但是有 b 后,multiplier 不知道两个乘数是相同的,因此不会计算。
(define (squarer-x a b)
;不能由 b 推得 a, multiplier 中没有定义
(multiplier a a b))
常数的约束条件相对而言简单一些,基本上就是为连接器设置约束,然后为其设置值即可。
(define (constrant value connector)
(define (me request)
(error "Unknown request" request))
(connect connector me)
(set-value! connector value me)
me)
这里比较有意思的一个约束是 probe,其被用来实现当值改变时进行打印,以简化调试过程。
(define (probe name connector)
(define (print-probe value)
(printf "Probe: ~s = ~s\n" name value))
(define (me request)
(cond ((eq? request 'I-have-a-value)
(print-probe (get-value connector)))
((eq? request 'I-lost-my-value)
(print-probe "?"))
(else (error "Unknown request" request))))
(connect connector me)
me)
最后,我们来实现这个连接器的数据抽象,连接器应该包含三个状态:值、来源和链接器的约束条件表。这里 set-my-value 用于设置值和来源,并且对所有约束条件调用以传播约束。forget-my-value 用来清空值和来源,并且对所有约束条件调用以传播约束。connect 用于插入约束条件。
;连接器构造函数:维护内部三个对象:值、来源以及此连接器的若干约束
(define (make-connector)
(let ((value #f) (informant #f) (constraints '()))
(define (set-my-value newval setter)
(cond ((not (has-value? me))
;如果没有值,则设置值与来源,且回调所有其它约束
;此处的 me 相当于 Java Class 中的 this
;这里本质就是调用 (if informant #t #f)
;不过是通过选择函数调用的,绕了一圈
(set! value newval)
(set! informant setter)
(for-each-except setter
inform-about-value
constraints))
((not (= value newval))
;如果已有值,且还需要设置新值,则直接报冲突
(error "contradiction" (list value newval)))
(else 'ignored)))
(define (forget-my-value retractor)
(if (eq? retractor informant)
;只有设置值的来源可删除值,删除来源并回调其它约束
(begin (set! informant #f)
(for-each-except retractor
inform-about-no-value
constraints))
'ignored))
(define (connect new-constraint)
;如果连接器尚不存在此约束,则将其插入到约束列表
;如果当前没有值,则回调约束们设置值
(if (not (memq new-constraint constraints))
(set! constraints
(cons new-constraint constraints)))
(if (has-value? me)
(inform-about-value new-constraint))
'done)
(define (me request)
(cond ((eq? request 'has-value?)
(if informant #t #f))
((eq? request 'value) value)
((eq? request 'set-value!) set-my-value)
((eq? request 'forget) forget-my-value)
((eq? request 'connect) connect)
(else (error "unknown op " request))))
me))
(define (for-each-except exception procedure list)
;对于 list 遍历,除了 exception 之外的执行 precedure 过程
(define (loop items)
(cond ((null? items) 'done)
((eq? (car items) exception) (loop (cdr items)))
(else (procedure (car items))
(loop (cdr items)))))
(loop list))
;连接器选择函数:用于操作值,为连接器添加新约束
(define (has-value? connector)
(connector 'has-value?))
(define (get-value connector)
(connector 'value))
(define (set-value! connector new-value informant)
((connector 'set-value!) new-value informant))
(define (forget-value! connector retractor)
((connector 'forget) retractor))
(define (connect connector new-constraint)
((connector 'connect) new-constraint))
(define (inform-about-value constraint)
(constraint 'I-have-a-value))
(define (inform-about-no-value constraint)
(constraint 'I-lost-my-value))
下面是 (define a (make-connector)) (define a (make-connector)) 和 (set-value! a 10 'user) 的环境表示:
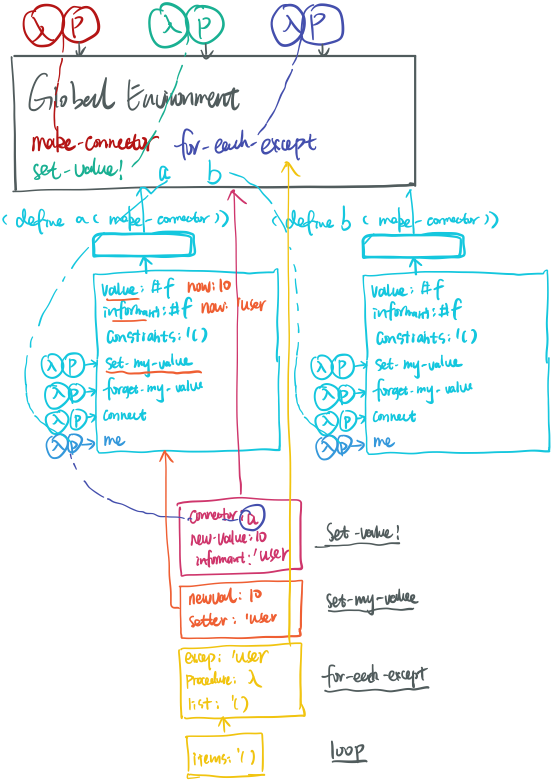
注意,在上面的摄氏度和华氏度转换的例子中,我们还可以更有表达式风格一些(表达式风格简洁易懂,不过缺点是丢失了句柄 —— 即操作这些连接器的机会,比如为中间连接器加上 probe 调试打印约束),而不是手动的一个一个构造连接器并加入约束体统:
;9C = 5(F-32) -> F = (9/5)C + 32
(define (celsius-fahrenheit-converter x)
(c+ (c* (c/ (cv 9) (cv 5)) x) (cv 32)))
(define C (make-connector))
(define F (celsius-fahrenheit-converter C))
(define (c+ x y)
(let ((z (make-connector)))
(adder x y z) z))
(define (c- x y)
(let ((z (make-connector)))
(adder y z x) z))
(define (c* x y)
(let ((z (make-connector)))
(multiplier x y z) z))
(define (c/ x y)
(let ((z (make-connector)))
(multiplier y z x) z))
(define (cv value)
(let ((z (make-connector)))
(constrant value z) z))
并发:时间是一个本质问题
上述基于环境模型的数据和过程抽象实现的两个应用:事件模拟的数字电路、约束系统充分展示了具有内部状态的环境对象在模拟上的威力。但是这种威力也付出了响应的代价:其不得不抛弃简单易懂的代换模型,丧失了同一性的同时带来了无穷尽的变化,且因为丢掉的应用透明性导致共享不再安全可靠,开发者必须把握一个或多个过程在时间维度实际执行的过程,心智负担加重。这些问题的本质在于为程序引入了时间这一维度:仅仅因为引入了时间,对一个表达式的求值结果不但依赖表达式本身,还依赖其发生的时刻。但介于其在模拟系统上的强大威力,因此环境模型也能得到大量使用。
但如果我们试图降低不必要的时间约束,将模型组织为相互分离的局部状态的对象,以实现更好的模块化和更高效的进行运行和模拟,换言之 —— 把计算模型划分为能够独立并发演化的部分(并发系统),问题就会暴露出来:这种独立局部状态的对象模块在并发上不得不面对更加严重的赋值状态复杂性问题。
从表面上看,时间是一个很简单的东西,就是强加在各个事件上的一个顺序,但其实其隐藏着巨大的复杂性,尤其是在并发系统中。这种复杂性的一般表现是:几个进程有可能同时共享一个状态变量,而导致复杂的原因是,多个进程可能同时操纵这种共享的状态,而操纵共享状态带来的复杂性的根源在于,对不同进程之间共享的变量的赋值,以及这种赋值不能立刻传递到各个进程导致状态的不一致。
比如银行账户,对于并发最严厉的限制是修改任意共享变量的两个操作不能同时存在:对于一个账户,同一时间只能一个人存款或取款,这样的效率很低。对于并发稍微放松一点限制,独立账户(非共享变量)可以并发执行,且一个共享账户允许并发读,但只允许同步写,这种方式导致可能有不同的顺序,但最终的结果一致。一些其它的技术,比如无锁编程和 CAS 技术能够进一步提升并发操作的效率且保证并发操作结果和顺序操作结果最终一致。而更弱的限制在特殊的场景中也有体现,比如热量流动模拟,每次并发更新值后,都会和相邻进程的值平均以修正,使其最终可以收敛到正确的解。
假定 parallel-execute 可以并发的执行多个放在入参的无参 lambda 表达式,make-serializer 可以实现串行化,串行化组将保证同一时间最多只有一个过程执行:(serializer λ) 将返回包装后的 λ 以供实际调用,在 (serializer λ) 过程中,通过操纵 serializer 内部的 mutex 互斥锁实现加锁和解锁,因此对于包装后的过程而言,同一时间只能有一个线程能够成功传入参数并获取锁使用。
(define (parallel-execute . args) ???)
(define (make-serializer) ???)
下面是两个例子,注意对于 x 而言,并发执行共享变量写入将导致各种可能结果,这里不仅仅是这两个 lambda 表达式执行先后的结果,而且指的是每个 lambda 表达式执行时获取第一个 x,第二个 x(第三个 x)以及更新 x 这三个(四个)步骤的彼此可能重叠,根据环境模型,x 的值来自于全局环境,因此这里完全可以出现执行 double 时第一个 x 为 10,然后中断,执行第二个表达式后,第二个 x 变为 1000 最后写入 x 为 10000 这样的事情。
(define x 10)
(parallel-execute (lambda () (set! x (* x x)))
(lambda () (set! x (* x x x))))
对于串行化保护而言,对于下面第一种保护方式仅仅让 s 传入的两个表达式实现了串行化,换言之,对于第一个表达式存在着计算 double x 和设置 x 两个步骤,第二个表达式存在着将 x 递增 1 的步骤,这三个步骤还是可能存在竞赛的。
(define x 10)
(define s (make-serializer))
(parallel-execute (lambda () (set! x ((s (lambda () (* x x))))))
(s (lambda () (set! x (+ x 1)))))
下面是一个正确的例子,传入 s 的表达式调用将串行执行,对共享变量的读写没有竞赛。
(define x 10)
(define s (make-serializer))
(parallel-execute (s (lambda () (set! x (* x x))))
(s (lambda () (set! x (* x x x)))))
基于上面的 API,银行账户的并发安全实现可以这样做:
(define (make-account balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((protected (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) (protected withdraw))
((eq? m 'deposit) (protected deposit))
((eq? m 'balance) balance)
(else (error "Unknown request " m))))
dispatch))
注意,就左图而言,对读取 balance 进行串行保护是不必要的,因为多个读取 balance 的线程彼此间并不互相影响,至于写入 balance 的 withdraw 和 deposit,这种保护措施将完全不起作用。就右图而言,这里每次返回了同一个 protected-functionName 共享引用,而不是每次都重新构造一个,对于此处的 make-serializer 实现而言,其实没有任何区别,不论是共享引用一个现有的受保护包装函数还是每次构造一个受保护包装函数,这个包装函数内部总是通过操纵全 serializer 唯一的 mutex 进行加锁和释放,本质没有区别。

尽管串行化器解决了单个共享变量的并发访问问题,但是多个共享变量将变得更棘手。下面是一个简单过程,转账,因为这里仅涉及每个账户的单次操作,因此只用在每个账户内实现串行化即可(尽管这样的实现不健壮,比如扣了 from 的款,to 还没收到时系统崩溃了):
(define (transfer from to amount)
((from 'withdra) amount)
((to 'deposit) amount))
而另一些过程则没这么幸运了,比如 exchange 交换两个账户余额,这需要计算一个中间值,然后再对两个账户进行操作,这意味着 exchange 也需要实现串行化。解决方案是将 account 的 serializer 暴露出来,然后构造 exchange 的两个变量的串行化保护:
(define (exchange a1 a2)
(let ((diff (- (a1 'balance) (a2 'balance))))
((a1 'withdraw) diff) ((a2 'deposit) diff)))
(define (make-account-2 balance)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((balance-serializer (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
((eq? m 'balance) balance)
((eq? m 'serializer) balance-serializer)
(else (error "Unknown request " m))))
dispatch))
(define (exchange a1 a2)
(let ((diff (- (a1 'balance) (a2 'balance))))
((a1 'withdraw) diff) ((a2 'deposit) diff)))
(define (exchange-safe a1 a2)
(let ((s1 (a1 'serializer))
(s2 (a2 'serializer)))
((s1 (s2 exchange)) a1 a2)))
基于这个版本,现在存取款都需要手动调用此串行化实例来执行保护:
(define (deposit-safe account amount)
(let ((s (account 'serializer))
(d (account 'deposit)))
((s d) amount)))
注意现在我们为什么不使用内嵌的串行化实例来处理 withdraw 和 deposit,而仅在 excahnge 上使用外部串行化实例呢?如下所示:

这是因为 exchange-safe 调用的 exchange 使用了 withdraw 和 deposit,如果 withdraw 和 deposit 使用了内置的串行化器,这意味着将 exchange-safe 外部的串行化器将包裹内部的这些串行化器,导致死锁。
现在,我们需要想办法实现 make-serializer 序列化器,可以基于 mutex 互斥锁的概念实现,mutex 是一种数据结构,其可以获取或释放一个锁,如果某个线程获取了 mutex 的锁,那么只有等到其释放,其余线程才能获取这个锁,否者将一直等待,基于此 make-serializer 的实现基本上就是在执行无参 lambda 前后加锁解锁。而 mutex 的实现这里给了实例,通过一个内部布尔变量来实现,如果已经有锁,那么无限循环请求 acquire,直到锁被释放。需要注意,这里 test-and-set! 仅用于示意,实际依赖于硬件实现原子化操作,否者两个线程同时进入 test-and-set! 同时获取到锁就会导致问题。
(define (make-serializer)
(let ((mutex (make-mutex)))
(lambda (p)
(define (serialized-p . args)
(mutex 'acquire)
(let ((val (apply p args)))
(mutex 'release)
val))
serialized-p)))
(define (make-mutex)
(let ((cell (list #f)))
(define (the-mutex m)
(cond ((eq? m 'acquire)
(if (test-and-set! cell)
(the-mutex 'acquire)))
((eq? m 'release) (clear! cell))))
the-mutex))
(define (clear! cell) (set-car! cell #f))
(define (test-and-set! cell)
(if (car cell) #t
(begin (set-car! cell #t) #f)))
信号量是一种类似于 mutex 互斥锁的结构,其可以被 n 个线程持有。其内部维护了 n 这个状态,每次请求锁就减 1,到 0 时无限循环等待释放锁。为了安全,这里在操作内部状态时通过 mutex 实现了加锁和释放。另一种解决方案是通过 test-and-set! n 这个原子操作(示意,依赖于硬件)。
(define (make-semaphore n)
(let ((mutex (make-mutex)))
(define (the-semaphore m)
(cond ((eq? m 'acquire)
(mutex 'acquire)
(cond ((= n 0) (mutex 'release)
(the-semaphore 'acquire))
(else (set! n (- n 1))
(mutex 'release))))
((eq? m 'release)
(mutex 'acquire)
(set! n (+ n 1))
(mutex 'release))))
(the-semaphore)))
(define (make-semaphore-2 n)
(define (test-and-set! n)
(if (= n 0) #t (begin (set! n (- n 1)) #f)))
(define (the-semaphore m)
(cond ((eq? m 'acquire)
(if (test-and-set! n)
(the-semaphore 'acquire) 'ok))
((eq? m 'release)
(set! n (+ n 1)))))
(the-semaphore))
多个共享值的最大问题不在于并发安全实现的繁琐,而在于死锁问题。对于 serialized-exchange 过程,如果 A 操作 a1 和 a2 的同时,B 同时并发操作 a2 和 a1,则 A 将卡死在获取 a2 锁这一步,B 将卡死在获取 a1 锁这一步,每个进程都无穷尽的等待下去,这就是所谓死锁。避免死锁的一种方案是为不同加锁对象分配标识符,总是按照一定顺序进行加锁。换言之,Havender 1968 提出的避免死锁的一般性技术是:枚举共享资源,按顺序获取它们,对于无法避免的死锁,要求具备死锁恢复方法,要求进程能够退出死锁状态并重新尝试运行。
下面是基于带数字标记的账户实现,其 exchange 过程将比较两个账户数字标记,然后按照顺序来获取锁,以避免死锁问题。但有时候,死锁是无法避免的,而其根源就是无法按照顺序去获取锁,只能通过死锁恢复来避免死锁,比如账户现在具有关联账户功能,当余额不足会自动从关联账户消费,A 和 B 账务余额都不足,且都同时从对方账户扣费,这时其都试图获取对方的锁,而这依旧会造成死锁。
(define (make-account-3 balance n-id)
(define (withdraw amount)
(if (>= balance amount)
(begin (set! balance (- balance amount))
balance)
"Insufficient funds"))
(define (deposit amount)
(set! balance (+ balance amount))
balance)
(let ((balance-serializer (make-serializer)))
(define (dispatch m)
(cond ((eq? m 'withdraw) withdraw)
((eq? m 'deposit) deposit)
((eq? m 'balance) balance)
((eq? m 'serializer) balance-serializer)
((eq? m 'id) n-id)
(else (error "Unknown request " m))))
dispatch))
(define (exchange a1 a2)
(let ((diff (- (a1 'balance) (a2 'balance))))
((a1 'withdraw) diff) ((a2 'deposit) diff)))
(define (exchange-safe-3 a1 a2)
(let ((s1 (a1 'serializer))
(s2 (a2 'serializer)))
((if (> (a1 'id) (a2 'id))
(s1 (s2 exchange-1))
(s1 (s2 exchange-1)))
a1 a2))
总的来说,并发性、时间和通信的复杂性不是计算机系统的问题,而是计算机系统对于物理世界复杂性的一种反映。对于这个问题的解决,有一种方案称之为 Actor 模型,在 20 世纪被广泛用于电信行业的 Erlang 中(以及现在的 Java/Scala 的 Akka Platform 中),这种模型强调 Actor 对于人类行为的模拟:接受和发送的消息都是异步实现的,共享变量依赖对一个变量 keeper 的请求和消息接受,而此 keeper 通过信箱来强制实现并发访问的时间有序性,这从架构上避免了共享状态导致的问题(不过也带来了新的消息传递可靠性问题),Go 的 goroutine 通过 channel 实现了类似但使用更简单的消息共享,而目前业界的主流做法就是将复杂性控制在某个系统内,比如数据库系统,而在其他地方通过函数式风格的逻辑代码实现并发安全性。
流
模拟真实世界的现象时,通过对局部变量的赋值来表示真实世界时间的变化看起来非常自然,但在上面章节中提到的同一与变化、引用和共享安全、并发问题等等,无一不是这一“自然的决策”带来的代价。在本章节,我们将介绍一种称之为流的数据结构,其能够模拟一些带有状态的系统,同时不需要利用赋值或变动的数据。
流作为延时的表
在上一章,我们基于序列实现了很多公共过程抽象,认识到了将其作为界面可以解决大量的实际问题。但如果序列是基于表实现的,那么在很多时候,序列的抽象过程将面临时间和空间上及其低效的代价。比如求 10 - 100000 之内的第二个素数这样的问题,采用基于表的序列,我们首先要构造一个 100000 - 10 = 99990 长的表,然后进行 filter,这样的效率很低。即便不是这样极端的例子,就拿计算区间素数之和来说,迭代风格相比较基于序列的操作也要节省大量空间 —— 因为后者需要先构建一个长长的表,哪怕这个表使用的空间实际上不必须。

流是一种惰性的表,其仅包含表头的值,对于表尾数据则在需要时通过内置的闭包动作求得。下面是流作为数据抽象的定义,其中 cons-stream 等价于 (cons <a> (delay <b>)),这里的 delay 用于惰性包含一个动作,当调用 force 时才进行求值。delay 的实现很简单,其实就是一个 lambda 闭包,force 则就是对这个匿名 λ 求值,但为了高效实现 delay,可将其包含动作的闭包传入 memo-proc,如果已经求过值,那么 memo-proc 将现有结果直接返回,反之则求值并记住结果,以便重复调用时可直接返回。stream-null? 用于判断一个流是否为空,the-empty-stream 用于返回一个空的流。
(define-syntax cons-stream
(syntax-rules () ((_ a b) (cons a (delay b)))))
;(define (cons-stream a b) (cons a (delay b)))
(define (stream-car s) (car s))
(define (stream-cdr s) (force (cdr s)))
(define stream-null? null?)
(define the-empty-stream '())
(define (memo-proc proc)
(let ((already-run? #f) (result #f))
(lambda ()
(if (not already-run?)
(begin (set! result (proc))
(set! already-run? #t) result)
result))))
(define-syntax delay
(syntax-rules () ((_ exp) (memo-proc (lambda () exp)))))
(define (force x) (x))
基于 stream 的数据抽象,我们可以打造流版本(而非序列版本)的过程操作,stream-ref 用于返回第 n 个流的值,stream-map 用于对一个或多个流的每个数据进行映射,区别序列的 map,这里的映射是惰性的,并不立刻求值,而是直接返回(除了第一项),stream-filter 用于对流的内容进行过滤,也是惰性的(除了第一项)。stream-for-each 用于让流“强行勤快”起开,逐个求值并执行 proc 过程,其可用于 display-stream 打印流内容。
(define (stream-ref s n)
(if (= n 0) (stream-car s)
(stream-ref (stream-cdr s) (- n 1))))
(define (stream-map-simple proc s)
(if (stream-null? s) the-empty-stream
(cons-stream (proc (stream-car s))
(stream-map-simple proc (stream-cdr s)))))
(define (stream-map proc . argstreams)
(if (stream-null? (car argstreams))
the-empty-stream
(cons-stream
(apply proc (map stream-car argstreams))
(apply stream-map
(cons proc (map stream-cdr argstreams))))))
(define (stream-filter pred stream)
(cond ((stream-null? stream) the-empty-stream)
((pred (stream-car stream))
(cons-stream (stream-car stream)
(stream-filter pred (stream-cdr stream))))
(else (stream-filter pred (stream-cdr stream)))))
(define (stream-for-each proc s)
(if (stream-null? s) 'done
(begin (proc (stream-car s))
(stream-for-each proc (stream-cdr s)))))
(define (display-line x) (newline) (display x))
(define (display-stream s) (stream-for-each display-line s))
最后,我们实现了流版本的 Range,这里返回的流是惰性的,仅包含 low 这个值:
(define (stream-enumerate-interval low high)
(if (> low high) the-empty-stream
(cons-stream low (stream-enumerate-interval (+ low 1) high))))
在实现求范围第二个素数问题的时候,可直接使用流版本的 Range,这样就避免了 Range 不必要的表空间和时间消耗,流仅求值到第二个素数就停止了。
(define (stream-second-prime from to)
(define (prime? n)
(define (square x) (* x x))
(define (divides? a b) (= (remainder b a) 0))
(define (find-divisor n test)
(cond ((> (square test) n) n)
((divides? test n) test)
(else (find-divisor n (next test)))))
(define (next n) (+ n 1))
(define (smallest-divisor n)
(find-divisor n 2))
(= n (smallest-divisor n)))
(car (cdr (stream-filter prime?
(stream-enumerate-interval from to)))))
下面的例子仅打印了 0,在获取第 5 项时打印了 0 - 5,在获取第 7 项时打印了 1- 7(如果没有使用 memo 实现 delay) 5 - 7(如果使用 memo 实现 delay),证明了 x 确实是惰性的(注意,这里的惰性指的是后面的数不计算,但就像不使用 memo 实现的 delay 一样,只包含 0 的 x 在求第 5 个数时计算了 0 - 5,在求第 7 个数时计算了 0 - 7,这里的 x 始终仅包含第一个值,如果多次用到除了第一个的前面的值,其还是会重复计算的,因此大部分 Scheme 实现都缓存了流的值,使得多次调用也只计算一次)。
(define (show x) (printf "~s\n" x) x)
(define x (stream-map show (stream-enumerate-interval 0 10)))
(printf "~s\n" (stream-ref x 5))
(printf "~s\n" (stream-ref x 7))
Scheme 流缓存在缓存流前面计算过的数值时非常有用:比如如下代码,accum 用一种巧妙的方式实现了流调用的计数,通过 sum 反映了出来,第一次 seq 返回了 1,因为此时仅头部元素 1 被执行 accum,sum 为 1,而 y 执行后,sum 为 6,z 执行后,sum 为 15,这是因为它们的第一项都是非惰性的,要进行实际计算,这是不使用 memo 的版本的结果,而使用 memo 后,y 执行完 sum 为 6,z 执行完 sum 为 10,相比较 15 少的原因是,其在找到第一个能被 5 整除的元素时,除了 seq 第一项的前面元素都被缓存,因此不会触发 accum 和 sum 的变化,因此 sum 的值变化更少。
(define sum 0)
(define (accum x) (set! sum (+ x sum)) sum)
(define interval (stream-enumerate-interval 1 20))
(define seq (stream-map-simple accum interval))
(define y (stream-filter even? seq))
(define z (stream-filter (lambda (x) (= (remainder x 5) 0)) seq))
无穷流
无穷流就是咬着自己尾巴的蛇:蛇头就是函数入口,其返回一个流,流的首项元素是非惰性的,而流的下一项则又通过构造这个函数/回到蛇头来生产,比如 ones 生产无限序列 1,这是最简单的无穷流。stream-n 生产递增的整数,这里的要点在于流的下一项操纵构造蛇头的参数来实现值的递增。fibgen 用于返回斐波那契数列,这里构造的下一项为数列第二个数,同时准备下一个数为上一个数 + 这个数,以便再次生成下一项(第三个数)。以上三个过程 ones, ints 和 fibs 是依赖一条🐍的无穷流。此外,我们可以使用 stream-filter 和 stream-map 对无穷流进行变化,比如 no-sevens 用来过滤不能整除 7 的整数序列。

;; 1×🐍
(define ones (cons-stream 1 ones))
(define (stream-n n) (cons-stream n (stream-n (+ n 1))))
(define ints (stream-n 1))
(define (fibgen a b) (cons-stream a (fibgen b (+ a b))))
(define fibs (fibgen 0 1))
(display (stream-ref fibs 10)) (newline)
(define (divisible? x y) (= (remainder x y) 0))
(define no-sevens (stream-filter (lambda (x) (not (divisible? x 7))) ints))
(display (stream-ref no-sevens 100)) (newline)
我们可以利用一个无穷流来构造另一个无穷流,比如如下所示的 sieve 过程,其构造的无穷流依赖于传入的 stream 参数,返回此流的第一项,而 sieve 的下一项则通过将多个传入 stream 的元素进行 stream-filter 过滤后生成。这里 sieve 过滤的条件是传入 stream 的元素的下一项元素不能被上一项整除。通过这种方式返回的序列就是 primes 素数序列。总结来说,这种依赖一条🐍来构造另一条🐍的无穷流称之为 1.5 条🐍依赖。
;; 1.5×🐍
(define (sieve stream)
(cons-stream (stream-car stream)
(sieve (stream-filter
(lambda (x)
(not (divisible? x (stream-car stream))))
(stream-cdr stream)))))
(define primes (sieve (stream-n 2)))
(display (stream-ref primes 50)) (newline)
接下来的这些过程:evens,ints-2,fibs-2,primes-2,paratial-sums 则更进一步,构造这些无穷流时,其末项不仅咬着自己的蛇头,还依赖一条或多条甘于贡献的小蛇(这些小蛇可能是单独的流,或者是自身的影子)。比如这里的 add-stream 用于将两条流合并,evens 用来返回 2 的倍数的序列,这里看起来代码很简单,但其实并不容易理解,可以认为,构造 evens 末项的时候,其依赖于一条两倍于自己的流的首项,因此第二项返回了 2,而第三项则依赖于一条两倍于自己的流的第二项,因此返回了 4,因此最后是 2 4 8 16 的序列。ints-2 是基于 ones 无限流实现的递增流,这里的含义类似,从 ones 中取一项和自身第一项相加得到第二个末项,从 ones 中取一项和自身第 n-1 项相加得到第 n 个末项,因此就是 1 2 3 4 的序列。fibs-2 则更加巧妙的利用了自身的前若干项实现了斐波那契数列,这里的 stream-cdr 和 stream-car fibs-2 并不会导致锁死,原因是 fibs-2 恰好有两项前置的非惰性值。
;; 2×🐍
(define (add-stream s1 s2) (stream-map + s1 s2))
(define evens (cons-stream 1 (add-stream evens evens))) ;2 4 8 16
(define ints-2 (cons-stream 1 (add-stream ones ints-2)))
(define fibs-2 (cons-stream 0
(cons-stream 1 (add-stream (stream-cdr fibs-2) fibs-2))))
这里检验了 delay 的 memo 功能,如果使用 memo,则计算 fibs-2 10 只会消耗 8 次 add-stream 的加法运算,而不使用 memo 则会导致流前面除了非惰性项的重复计算,导致加法的指数增加。
(define test-sum 0)
(define (add-stream-debug s1 s2) (stream-map
(lambda (a b) (begin (set! test-sum (+ test-sum 1)) (+ a b))) s1 s2))
(define fibs-debug (cons-stream 0
(cons-stream 1 (add-stream-debug (stream-cdr fibs-debug) fibs-debug))))
(newline) (display (stream-ref fibs-debug 10))
(newline) (display test-sum)
scale-stream 和 add-stream 类似,实现了为流的每个数乘上某个值,其都依赖于底层的 stream-map 实现,可以将 scale 后的流看做单独的蛇,double 过程基于 scale-stream 进行了实现,每次从这条 scale 后的蛇上取元素构造自身下一项,然后自身又成为这条 scale 的蛇的下一项,因为 double 第二项对应着 scale-double 的第一项,因此通过 scale-double 构造 double 的第 n 项始终是可行的。当然,另一种实现方式就是使用单独的蛇,末项构造时通过对上一项进行 double 直接返回。
(define (scale-stream stream factor)
(stream-map (lambda (x) (* x factor)) stream))
(define double (cons-stream 1 (scale-stream double 2)))
primes-2 是利用这种双蛇模式计算素数流的实现方式,其依赖一条整数流,对这条整数流执行 prime? 过程以过滤并查找下一个素数作为末项。注意这里 prime? 过程并不同于一般过程,其会去通过 primes-2 这条蛇本身来获取元素进行检查(一个数 n 如果不能被任意小于 √n 的素数整除,那么它就是素数),自然,这里检查的元素一定都是 primes-2 已经计算得到的结果(而非惰性的部分)。
(define (prime? n)
(define (square x) (* x x))
(define (divides? a b) (= (remainder b a) 0))
(define (iter ps)
(cond ((> (square (stream-car ps)) n) #t)
((divides? n (stream-car ps)) #f)
(else (iter (stream-cdr ps)))))
(iter primes-2))
(define primes-2
(cons-stream 2 (stream-filter prime? (stream-n 3))))
mul-streams 和 div-streams 是类似于 add-streams 的对于两条流的合并处理,factorials 用于使用双蛇模式计算阶乘,由于每一个阶乘值都等于上一个阶乘值 * 这个值本身,因此这里“甘于贡献的小蛇”是整数流和 factorials 流的乘积。partial-sums 也是这种规律的流体现,对于整数 1 2 3 4 5,返回的 partial-sums 流(下称 ps 流)的每一个下一项都相当于当前 ps 流的值 + 原 stream 下一个值之和。
(define (mul-streams s1 s2) (stream-map * s1 s2))
(define (div-streams s1 s2) (stream-map / s1 s2))
(define factorials (cons-stream 1 (mul-streams factorials (stream-n 2))))
(define (partial-sums stream) ;S0 S0+S1; S0+S1+S2; ...
(cons-stream (stream-car stream)
(add-stream
(partial-sums stream)
(stream-cdr stream))))
(define par-sums (partial-sums ints)) ;1 3 6 10 15
merge 是一个将两个排序过的流合并为无重复流的过程,利用这个过程,我们可以计算所有满足“没有 2 3 5 以外的素数因子”的整数,即:满足条件的集合 S 从 1 开始,(scale-stream S 2) (scale-stream S 3) (scale-stream S 5) 的元素都是 S 的元素。这里的小蛇 (merge (scale S 2) (scale S 3)) 并不会咬到 S 自身,因此 S 可以持续的返回元素。
(define (merge s1 s2)
;将两个排好序的流合并为一个排好序的流并删除重复元素
(cond ((stream-null? s1) s2)
((stream-null? s2) s1)
(else
(let ((s1car (stream-car s1))
(s2car (stream-car s2)))
(cond ((< s1car s2car)
(cons-stream s1car (merge (stream-cdr s1) s2)))
((> s1car s2car)
(cons-stream s2car (merge s1 (stream-cdr s2))))
(else (cons-stream s1car
(merge (stream-cdr s1)
(stream-cdr s2)))))))))
(define S (cons-stream 1
(merge (merge (scale-stream S 2) (scale-stream S 3))
(scale-stream S 5))))
最后这个例子生动形象的展示了双流模式的应用:幂级数的加减乘除运算的实现。关于题目完整的描述参见下文:

(define (integrate-series a-stream)
(stream-map / a-stream ints))
(define exp-series
(cons-stream 1 (integrate-series exp-series)))
(define cosine-series (cons-stream 1
(integrate-series (scale-stream -1 sine-series))))
(define sine-series
(cons-stream 1 (integrate-series cosine-series)))
(define (mul-series s1 s2)
(cons-stream (* (stream-car s1)
(stream-car s2))
(add-stream (scale-stream (stream-cdr s2)
(stream-car s1))
(mul-series (stream-cdr s1) s2))))
(define (reciprocal-series s) (cons-stream 1
(mul-series (scale-stream (stream-cdr s) -1)
(reciprocal-series s))))
(define (div-series s1 s2)
(if (eq? (stream-car s2) 0)
(error "constant of s2 can't be zero." s2)
(mul-series s1 (reciprocal-series s2))))
流计算模式的应用
流可以用来表示时间,这样就避免了引入时间维度的可变状态导致的信息丢失问题。
将迭代过程表示为流过程
在迭代操作时,我们可以不在每次调用函数是传入新变量以维护可变状态,而是让函数作为无穷流获取下一项的过程,比如下面解决 sqrt 的过程,sqrt-stream 采用无限流,首项为第一次传入的 1.0,之后应用 sqrt-improve 作为末项,通过对流的打印或者取特定位置值就可以得到 sqrt-improve 的结果。注意这里的 sqrt-stream 中不要省略本地变量 guesses,如果省略,则每次流末项获取时都依赖一个新的 sqrt-stream 过程返回一个同样的但不是通一个引用的流,这将导致 delay 的 memo 机制失效,降低效率。
(define (average x y) (/ (+ x y) 2))
(define (sqrt-improve guess x)
(average guess (/ x guess)))
(define (sqrt-stream x)
(define guesses
(cons-stream 1.0
(stream-map (lambda (guess) (sqrt-improve guess x)) guesses)))
guesses)
(display (stream-ref (sqrt-stream 2) 100))
下面是使用 π/4 = 1 - 1/3 + 1/5 - 1/7 ... 求 π 的方案,pi-summands 中构造了每一个分式,然后合并流。最后进行了 4 倍放大,然后就得到了 π 的模拟流。不过这里的问题是,模拟的 π 值收敛的很慢。
(define (pi-summands n)
(cons-stream (/ 1.0 n)
(stream-map - (pi-summands (+ n 2)))))
(define pi-stream
(scale-stream (partial-sums (pi-summands 1)) 4))
(display (stream-ref pi-stream 10))
ln2 的计算是另外一个类似的例子:ln2 = 1 - 1/2 + 1/3 - 1/4 ...
(define (ln2-stream)
(define (ln2-summands n)
(cons-stream (/ 1.0 n)
(stream-map - (ln2-summands (+ n 1)))))
(partial-sums (ln2-summands 1)))
(print-stream-first (ln2-stream) 3)
我们可以考虑应用欧拉发现的对于交错级数和工作的加速器来加速递归,假如 Sn 是原有和的序列的第 n 项,那么加速后的形式就是:
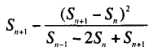
因此我们可以对原来的模拟流应用欧拉变换,得到更好的收敛效果。为了进一步进行加强,可以通过 make-tableau 构造生产流的流,第一行都是递归应用了 transform 后的加强版,这里去除序列第 8 项就能获取到 π 的精确 14 位数字。
(define (square x) (* x x))
(define (euler-transform s)
(let ((s0 (stream-ref s 0))
(s1 (stream-ref s 1))
(s2 (stream-ref s 2)))
(cons-stream (- s2 (/ (square (- s2 s1))
(+ s0 (* -2 s1) s2)))
(euler-transform (stream-cdr s)))))
(display (stream-ref (euler-transform pi-stream) 10))
(define (make-tableau transform s)
(cons-stream s (make-tableau transform (transform s))))
(define (accelerated-sequence transform s)
(stream-map stream-car (make-tableau transform s)))
(display (stream-ref (accelerated-sequence euler-transform pi-stream) 8))
流能够提供的功能迭代也能够提供,但是流带给我们一种操纵“无穷”的数据结构的能力 —— 如果我们想要将流看做一种数据抽象而非隐藏在一个过程中的迭代的话(这种流数据抽象使得这种描述数据操作的方式更容易实现),在上面的 transform 和 make-tableau 上淋漓尽致的得以体现。
下面的 stream-limit 展示了如何从流中选取可容忍误差范围的结果,stream-limit-x 很优雅的操纵流这种数据结构,但是不满足这里的应用场景,这是流的场景局限。
(define (stream-limit-x stream tolerance)
(define tol-stream
(add-stream (scale-stream (stream-cdr stream) -1) stream))
(define filtered-tol-stream
(stream-filter
(lambda (x) (if (< (abs x) tolerance) #t #f)) tol-stream))
(stream-ref filtered-tol-stream 0))
(define (stream-limit stream tolerance)
(if (< (abs (- (stream-ref stream 0)
(stream-ref stream 1))) tolerance)
(stream-ref stream 1)
(stream-limit (stream-cdr stream) tolerance)))
(define (sqrt x tolerance)
(stream-limit (sqrt-stream x) tolerance))
序列的无穷流
上面介绍的使用流来表示迭代过程并没有真正表现出流的优势,但是在一些场景下,比如需要对无穷或者为止长度的数据执行操作,这时候使用迭代就很不合适(随着现代计算机需要处理的数据越来越多,这种场景变得非常常见)。在这一部分,我们将试图将两条或多条流构造为序对流,注意,这里不是指的将两条流每个元素配对,而是对每个流的每个元素和另外一条流的所有元素配对,因为流是无限的,因此使用迭代无法解决这样的问题 —— 甚至使用流也比较棘手。假设 S 和 T 是两条待整合的流,那么其序对有如下左图种方式,如果不考虑顺序,那么一共有右图所示个元素。
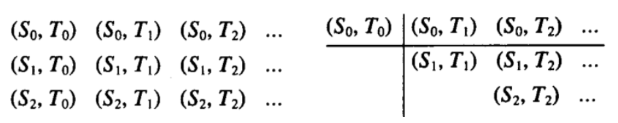
这里的模式其实很明显,序对的流首项是: S 第一个元素 和 T 第一个元素,末项是:S 第一个元素作用于 T 剩下的元素(第一行)+ 递归调用此过程,传入 S 剩下的元素和 T 剩下的元素。但问题是,末项两个流之和如何相加,根据 append 我们定义 stream-append,但是这不能解决问题,因为 stream-append 获取 s1 第一项后,下一项总是试图遍历尽 s1 下一项,直到 s1 完毕再遍历 s2,对于一般流而言,这不是问题,且很好的符合 append 的语义,但是对于两条无限流,这样就永远停留在 s1 上,不会到达 s2,就这个例子而言,就是停留在第一行。
(define (stream-append s1 s2)
(if (stream-null? s1) s2
(cons-stream (stream-car s1)
(stream-append (stream-cdr s1) s2))))
这个问题其实很容易解决,递归时将两条流顺序交换即可,这样就会“雨露均沾” 的将两条流串起来了。
(define (interleave s1 s2)
(if (stream-null? s1) s2
(cons-stream (stream-car s1)
(interleave s2 (stream-cdr s1)))))
基于 interleave 和上面的模式,可以提供 pairs 过程,其返回序对流:
(define (pairs s t)
(cons-stream (list (stream-car s)
(stream-car t))
(interleave (stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
(pairs (stream-cdr s) (stream-cdr t)))))
(print-stream-first (pairs ints ints) 10)
注意,不能写成 pairs-x 的形式,如下所示,这是因为 interleave 并不是 cons-stream,没有 delay 第二个参数的能力,因此这里虽然理论可以成功获取第一个元素,但构造甚至不会返回,因为 Scheme 总是试图对传入 interleave 的第二个表达式求值,而这是一个无穷的递归。
(define (pairs-x s t)
(interleave (stream-map (lambda (x) (list (stream-car s) x)) t)
(pairs-x (stream-cdr s) (stream-cdr t))))
对于考虑顺序的 pairs,实现也很简单,只需要在返回末项是第二行从头开始即可:
(define (pairs-dup s t)
(cons-stream (list (stream-car s)
(stream-car t))
(interleave (stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
(pairs-dup (stream-cdr s) t))))
当然,两条流的序对可以做,那么三条流自然也不在话下,triples 提供了三条流的合并,这里巧妙的利用了 pairs t u 返回 t 和 u 组成的所有序对,用于配合 interleave 构造第一行(将 t u 合并起来看),然后相似的递归调用 triples 第二行即可。另一种看法是将其看做正方体,需要求的序对本质是一个三棱锥。phythagorean-stream 提供了一个满足三元序对前两个元素平方和等于第三个元素平方的序对,比如 3 4 5、6 8 10 等,这种能力只有基于流才能实现。
(define (triples s t u)
(cons-stream (list (stream-car s) (stream-car t) (stream-car u))
(interleave (stream-map (lambda (x) (cons (stream-car s) x))
(stream-cdr (pairs t u)))
(triples (stream-cdr s)
(stream-cdr t)
(stream-cdr u)))))
(define phythagorean-stream
(stream-filter (lambda (items)
(let ((i (car items)) (j (cadr items)) (k (caddr items)))
(= (+ (* i i) (* j j)) (* k k)))) (triples ints ints ints)))
(print-stream-first phythagorean-stream 3)
在上面的例子中,我们随机穿插了合并为序对的流的顺序,但有时我们可能希望通过权重函数自行定义,merge-weighted 是 merge 的一个变式,其将两个流根据 weight 权重函数的结果来进行排序合并。
(define (merge-weighted s1 s2 weight)
(cond ((stream-null? s1) s2)
((stream-null? s2) s1)
(else (let ((s1car (stream-car s1))
(s2car (stream-car s2)))
(let ((comp (- (weight s1car) (weight s2car))))
(cond ((< comp 0)
(cons-stream s1car
(merge-weighted (stream-cdr s1) s2 weight)))
((> comp 0)
(cons-stream s2car
(merge-weighted s1 (stream-cdr s2) weight)))
(else (cons-stream s1car
(cons-stream s2car
(merge-weighted (stream-cdr s1)
(stream-cdr s2) weight))))))))))
基于 merged-weight 过程,我们完全可以将 pairs 合并第一行和剩余行的任务交给 merged-weight 来实现,其并不会像 stream-append 一样,因为这里总是排过序的(按照权重),因此会自然的按照权重来从两条流中按权重顺序返回序对流。
(define (weighted-pairs s t weight)
(cons-stream
(list (stream-car s) (stream-car t))
(merge-weighted
(stream-map (lambda (x) (list (stream-car s) x)) (stream-cdr t))
(weighted-pairs (stream-cdr s) (stream-cdr t) weight) weight)))
pascal 是一个二元序对流,这里的序对按照和的大小进行了排序。sorted-number235 是一个二元序对流,这里的序对每个值都可以被 2 3 5 整除,且其按照序对第一个元素 * 2 + 第二个元素 * 3 + 第一个元素 * 第二个元素 * 5 的和的顺序进行排序。
(define (divide? a b) (= (remainder a b) 0))
(define pascal (weighted-pairs ints ints (lambda (p) (apply + p))))
(define number235 (stream-filter
(lambda (x) (not (or (divide? 2 x) (divide? 3 x) (divide? 5 x)))) ints))
(define sorted-number235 (weighted-pairs number235 number235
(lambda (p)
(+ (* 2 (car p)) (* 3 (cadr p)) (* 5 (car p) (cadr p))))))
ramanujan 数指的是可以以多于一种方式表达为两个立方数之和的数,ramanujan 过程则返回了这样的数,其实现并不复杂,对于序对流,只需要按照两个元素分别立方和排序,那么相邻的数都是某个 ramanujan 数的表达方式,ram-pair 构造一个流,流通过错序对两个数计算 ram-weight 以判断其是否权重相等,如果相等,则就得到一个 ramanujan 数,将其作为流元素弹出,通过 stream-map ram-weight ram-fit-stream 将此流重映射为权重值,即得到了 ramanujan 数的流。ramanujan-for 用来检查某个数是否是 ramanujan 数,且如果是,返回它的多种表达方式流,其原理类似。
(define (ramanujan)
(define ram-weight (lambda (x)
(let ((i (car x)) (j (cadr x))) (+ (* i i i) (* j j j)))))
(define ram-stream (weighted-pairs ints ints ram-weight))
(define (ram-pair s1 s2)
(let ((i1 (stream-car s1)) (i2 (stream-car s2)))
(if (= (ram-weight i1) (ram-weight i2))
(cons-stream i1 (ram-pair (stream-cdr s1) (stream-cdr s2)))
(ram-pair (stream-cdr s1) (stream-cdr s2)))))
(define ram-fit-stream (ram-pair (stream-cdr ram-stream) ram-stream))
(stream-map ram-weight ram-fit-stream))
(define (ramanujan-for t)
(define ram-weight (lambda (x)
(let ((i (car x)) (j (cadr x))) (+ (* i i i) (* j j j)))))
(define ram-stream (weighted-pairs ints ints ram-weight))
(stream-filter (lambda (x) (= (ram-weight x) t)) ram-stream))
同样的,我们可以得到“所有数都能够以三种不同的方式表示为两个平方数之和”的这些不同的表示方式,和 ramanujan 不同的是,这里的 way3 对按照权重排过序的流的三个元素进行检查,相邻三个元素意味着找到一个解,将其作为 list 扔出去即可,因此 way3 就得到了目标流(每个流的元素都是不同表示方式的序列)。
(define (number-3way)
(define n-weight (lambda (x)
(let ((i (car x)) (j (cadr x))) (+ (* i i) (* j j)))))
(define n-stream (weighted-pairs ints ints n-weight))
(define (way3 s1 s2 s3)
(let ((i1 (stream-car s1)) (i2 (stream-car s2)) (i3 (stream-car s3)))
(if (and (= (n-weight i1) (n-weight i2))
(= (n-weight i3) (n-weight i2)))
(cons-stream (list (n-weight i1) i1 i2 i3)
(way3 (stream-cdr s1) (stream-cdr s2) (stream-cdr s3)))
(way3 (stream-cdr s1) (stream-cdr s2) (stream-cdr s3)))))
(way3 (stream-cdr (stream-cdr n-stream))
(stream-cdr n-stream)
n-stream))
将流作为信号
如果说局部状态以及其带来的模块性是物理世界的一种形象表征,那么流则就是信号处理系统在计算中的对应物,流的元素可以表示信号在顺序上的时间间隔值。 因为流的性质,所以积分过程很容易实现,如下所示 S 的流可以简单的对 x 在时间维度流的积累加上常数 C 得到,integral 过程实现了这一点。如果将这一过程看做信号处理系统,则其表示如下:
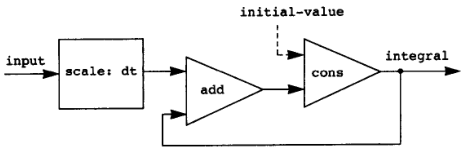
(define (integral integrand initial-value dt)
(define int
(cons-stream initial-value
(add-stream (scale-stream integrand dt) int))) int)
根据这个积分过程,可以很容易实现 RC 电路(R 电阻 C 电容)的信号模拟,其中 i 为输入电流,v 为响应电压,其关系为:
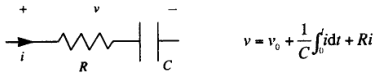
下面提供了其基于积分的实现:
(define (RC R C dt) (lambda (i v0)
(add-stream
(integral (scale-stream i (/ 1 C)) v0 dt)
(scale-stream i R))))
(define RC1 (RC 5 1 0.5))
(print-stream-first (RC1 ones 10) 10)
下面是另一个例子,对于信号 1 2 1.5 1 0.5 -0.1 -2 -3 .. ,另一个描述了此信号过零点的信号如下所示: 0 0 0 0 0 -1 0 0 (从正到负为 -1,从负到正为 1,其余为 0)。下面是这个过零点信号的实现:
(define (make-zero-crossings input-stream last-value)
(cons-stream
(sign-change-detector (stream-car input-stream) last-value)
(make-zero-crossings (stream-cdr input-stream)
(stream-car input-stream))))
(define (sign-change-detector new init)
(cond ((and (< init 0) (> new 0)) 1)
((and (> init 0) (< new 0)) -1)
(else 0)))
(define sense-data ints)
(define zero-crossings (make-zero-crossings sense-data 0))
本质来说,这里就是将流前后两个信号比较生成新的流,因此可以写的更加简洁:
(define zero-crossings-boss
(stream-map sign-change-detector
sense-data (cons-stream 0 sense-data)))
因为某些时候传感器会有噪声,可能产生假的过零点,因此可以对信号进行平滑,下面的代码展示了对于每个感应值和前一个平均后再提取过零点值的过程:
(define (make-zero-crossings-exp input-stream last-value last-avpt)
(let ((avpt (/ (+ (stream-car input-stream) last-value) 2)))
(cons-stream (sign-change-detector avpt last-avpt)
(make-zero-crossings-exp (stream-cdr input-stream)
avpt))))
但是这个例子并不优雅,因为平均过程被耦合在其中了,下面的代码将平均过程提取了出来,先对原始数据做平滑,然后求过零点流。
(define (make-zero-crossings-module input-stream)
; (define (smooth s)
; (cons-stream (/ 2 (+ (stream-car s) (stream-car (stream-cdr s))))
; (smooth (stream-cdr s))))
(define (smooth s)
(stream-map (lambda (a b) (/ (+ a b) 2)) s (stream-cdr s)))
(define after-smooth (smooth input-stream))
(stream-map sign-change-detector
after-smooth (stream-cdr after-smooth)))
流和延迟求值
流能够实现的本质得益于延迟求值 - delay 和 fouce 的实现。虽然我们构造的流抽象在大部分情况下可以很好的工作,但是在某些复杂的情况下,可能还是需要直接使用 delay,比如如下一个求解 dy/dt = f(y) 的解微分方程,这里的实现 integral 需要传入一个用于积分的流,但是这个流依赖于对积分结果应用函数 f 得到的结果,因为这里实际上 integral 第一次返回的是 y0,所以我们可以将传入 integral 的 dy 先 delay 掉,然后在 integral 中 force 进行计算。这里展示了 dy/dt = y 的解(e)。

(define (integral-lazy delayed-integrand initial-value dt)
(define int
(cons-stream initial-value
(let ((integrand (force delayed-integrand)))
(add-stream (scale-stream integrand dt) int))))
int)
(define (solve f y0 dt)
(define y (integral-lazy (delay dy) y0 dt))
(define dy (stream-map f y)) y)
(display (stream-ref (solve (lambda (y) y) 1 0.001) 1000))
integral 还可以使用不使用 add-stream 的一般方式定义,为了实现懒加载,这里也需要假定 integrand 传入流为 delay,然后对其先 fouce 再使用:
(define (integral-2 integrand-delay initial-value dt)
(cons-stream initial-value
(let ((integrand (force integrand-delay)))
(if (stream-null? integrand)
the-empty-stream
(integral-2 (delay (stream-cdr integrand))
(+ (* dt (stream-cdr integrand))
initial-value)
dt)))))
对于齐次二阶线性微分方程而言,下面是一个信号图:
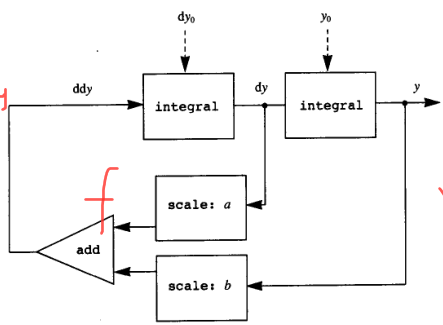
可以类似的写出 y 的求解方式,注意这里使用了两次 delay,分别对 dy 和 ddy。
(define (solve-2nd a b dt y0 dy0)
(define y (integral-lazy (delay dy) y0 dt))
(define dy (integral-lazy (delay ddy) dy0 dt))
(define ddy (add-stream (scale-stream a dy)
(scale-stream b y)))
y)
可以抽象出来,使过程可以解决一般的二次微分方程
(define (solve-2nd-common f dt y0 dy0)
(define y (integral-lazy (delay dy) y0 dt))
(define dy (integral-lazy (delay ddy) dy0 dt))
(define ddy (f dy y))
y)
最后看一个串联 RLC 电路的例子,这里 R L C 分别是电阻、电容和电感值,根据下面的信号流图,可以使用流来轻松的进行表达,RLC 过程以 R L C 和 dt 为参数,返回一个过程,此过程以初始时间的 vc 和 il 电压和电流为参数,返回关于电压和电流随时间变化的流,这里 vc 依赖 il 而 il 也依赖 vc。
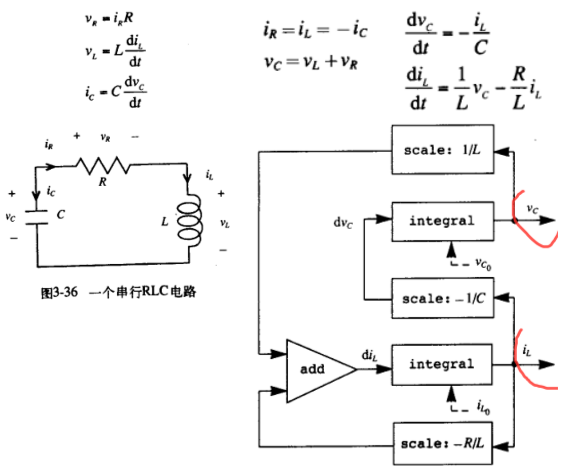
(define (RLC R L C dt)
(lambda (vc0 il0)
(define vc (integral-lazy (delay (scale-stream (* -1 (/ 1 C)) il))
vc0 dt))
(define il (integral-lazy (delay (add-stream
(scale-stream (/ 1 L) vc)
(scale-stream (* -1 (/ R L)) il)))
il0 dt))
(stream-map cons vc il)))
(define RLC1 (RLC 1 1 0.2 0.1))
(print-stream-first (RLC1 10 0) 5)
如上所示,虽然流在信号模拟方面一点也不逊色于可变状态的方式,但是流的显式延迟求值分裂了过程,我们需要小心确认每个参数到低是延迟的还是常规的,为避免这一问题,一种方式让所有过程都应用延时参数,即采用规范序方式(而非正则序),但是延迟导致了依赖事件顺序的能力受到极大损害,在赋值、变动数据和执行 IO 的过程将非常难以理解。
总的来说,引入赋值的主要好处就是可以增强系统的模块化,在本章开头的求解 π 的蒙卡罗特过程中得以体现:赋值将一个大系统的状态分别封装,隐藏到局部变量中。在流模型中,可以实现等价的模块化,同时不需要赋值,比如这里 rand-stram 的实现:
(define (random-update x) (remainder (+ (* 13 x) 5) 24))
(define random-init (random-update (expt 2 32)))
(define rand-state
(let ((x random-init))
(lambda () (set! x (rand-update x)) x)))
(define rand-stream
(cons-stream random-init
(stream-map rand-update stream)))
回到本章开头的一些例子,我们现在可以使用流来实现蒙卡罗特过程,map-successive-pairs 对两个随机数进行操作,返回结果,cesaro-stream 是其一个应用,用于计算是否两个数有公共因子,monte-calrlo 过程在这里没有使用赋值和局部变量,而是依靠传入的结果流实现了概率统计,其返回概率随时间的变化。根据这些过程,pi 可以轻易的通过 cesaro-stream 配合 monte-calorlo 统计得以实现计算。
(define (gcd a b) (if (= b 0) a (gcd b (remainder a b))))
(define (map-successive-pairs f s)
(cons-stream
(f (stream-car s) (stream-car (stream-cdr s)))
(map-successive-pairs f (stream-cdr (stream-cdr s)))))
(define cesaro-stream
(map-successive-pairs (lambda (r1 r2) (= (gcd r1 r2) 1))
rand-stream))
(define (monte-calrlo experiment-stream passed failed)
(define (next passed failed)
(cons-stream (/ passed (+ passed failed))
(monte-calrlo
(stream-cdr experiment-stream) passed failed)))
(if (stream-car experiment-stream)
(next (+ passed 1) failed)
(next passed (+ failed 1))))
(define pi (stream-map (lambda (p) (sqrt (/ 6 p)))
(monte-calrlo cesaro-stream 0 0)))
蒙卡罗特积分过程类似,和基于赋值的过程不同,这里通过计算随机点落在圆中的流在 monte-carlo 过程进行统计,计算出了倍率,然后实现了积分。
(define (estimate-integral p x1 x2 y1 y2 trials)
(define (random-in-range low high)
(let ((range (- high low)))
(+ low (random range))))
(define circle-x (+ (/ (- x2 x1) 2) x1))
(define circle-y (+ (/ (- y2 y1) 2) y1))
(define (double x) (* x x))
(define integral-stream
(map-successive-pairs
(lambda (x y)
(not (> (+ (double (- x circle-x))
(double (- y circle-y)))
(double 1))))
rand-stream))
(scale-stream (monte-carlo integral-stream 0 0)
(* (- x2 x1) (- y2 y1))))
当然,支持重置的随机数生成器也是可以实现的,这里巧妙的利用了传入命令:生成 or 重置作为命令流,通过对命令流的 map 调用 rand-update 实现了随机数和可重置的随机数生成器。
(define (rand requests)
(define (update cmd data)
(cond ((eq? cmd 'generate)
(rand-update data))
((and (pair? cmd)
(eq? (car cmd) 'reset)
(number? (cadr cmd)))
(cadr cmd))))
(define requested-stream
(cons-stream random-init
(stream-map update requests requested-stream)))
requested-stream)
(define (list->stream items)
(if (null? items) the-empty-stream
(cons-stream (car items)
(list->stream (cdr items)))))
(define (stream->list stream)
(if (stream-null? stream) '()
(cons (stream-car stream)
(stream->list (stream-cdr stream)))))
(stream->list
(rand (list->stream '(generate generate (reset 5) generate (reset 5)))))
当然,不是所有的赋值都可以使用流来模拟,比如我们虽然可以基于流实现银行账户,不过却没有办法处理两个共享账户者对数据流的归并。使用对象、赋值和局部状态来进行模拟是自然的,因为这本质是使用计算执行的时间来模拟我们所在世界的时间,也就是将“对象”弄进了计算机,非常符合我们队自己身处其中并交流的世界的看法。对象模型也是强大的,总的来说,当对象之间不共享的状态远远大于它们所共享的状态时,对象模型就特别好用(每个人都心怀鬼胎,但彼此和睦),反之,对象则成为一种对于数据和过程抽象的禁锢(看不到一件事情是如何发展的,见上一章末尾 - 无状态的面向对象中的数据抽象和过程抽象 部分)。