SICP 103 - 构造数据抽象
这是 SICP 第二章的内容总结,包含了大部分习题的答案。数据抽象是软件工程的基石之一,本文阐述了数据抽象的方法,如何对层次性数据进行抽象,如何对数据抽象的不同表现形式进行处理(基于标签、数据导向风格和消息传递风格),如何打造数据抽象层次这几个问题。
Hermann Weyl 在《思维的数学方式》中提到:现在到了数学抽象中最关键的一步:让我们忘记这些符号所表示的对象。.. 数学家不应该在这里停步,有许多操作可以应用于这些符号,而根本不必考虑它们到底代表着什么东西。这句话简要的概括出了编程中“数据抽象”的主要目的:创建一种不依赖特定数据类型的过程,使其可以满足更多不同的用例。
数据抽象导引
把“数据”看做一种简单认识,那么“复合数据”就是一种数据对象的组合的新认识,这种“复合数据”相比较“纯数值数据”而言,可以更好地模拟真实世界中具有若干侧面的现象,而不仅仅停留在操做基本数值的数学问题层面:比如一个操做有理数(分数)的运算,使用“纯数值数据”将不得不对分子和分母在每一个过程中手动对应并小心计算,而使用“复合数据”则可以将其看做一个概念单位进行操作。将“复合数据”和其他所有数据对比可以发现,“复合数据”是一种比语言提供的(或者说机器实际操作的)基本数据对象更高的概念层次,基于这种更高的抽象(过程可接受、直接操作复合对象的能力,所有过程基于此有理数的抽象进行过程计算,而非基于基本数据的抽象进行计算),我们可以提升程序的模块性(即在一个范围内随意修改实现而不影响依赖这些过程的其他过程的正确性的能力),此外还能进一步提升程序设计语言的表达能力(过程不仅不必关心参数的具体细节结构,甚至不用关心它们是什么复合数据结构 —— 只需要调用能处理这种复合数据结构的过程处理即可。就像网络栈,每个上层只依赖和其接触的层,而不依赖所有底层,或者说就像 OOP 的“依赖接口而非实现”的设计理念,这里的接口就是其接触层提供的抽象,实现就是其底层具体的细节)。
总的来说,数据抽象是一种设计方法学,其让我们将一个复合数据对象的使用和此对象怎样用更基本的数据对象构造的细节隔离开。基于这种更高的抽象平台,我们往往需要设计一些使用复合数据对象的程序,使其就像是在“抽象数据”上操作一样。此外,为了让“抽象数据”落地被机器执行,还需要一组被称之为选择函数和构造函数的过程来建立抽象数据的具体表示。
下面是一个例子,其中 cons 用于形成对偶,car 用于获取寄存器地址部分内容(对偶第一个),cdr 用于获取寄存器减量部分内容(对偶第二个)。这里展示了构造抽象数据的构造和选择函数(考虑到了归约和正负号问题),以及基于抽象数据平台的运算过程定义以及其使用方法。
注意到这里形成的“抽象屏障” rat 是如何让我们工作在一个较高层次的。
一般而言,为了让复合数据抽象被机器识别,我们要提供其构造和选择函数,在机器可理解的基本数值和复合抽象数据之间搭建桥梁。
这个桥梁一般在初始化此抽象数据、定义底层交互时使用,比如这里为 rat 数据抽象定义的 add, sub, mul, div, equal运算符。而之后的过程,则完全基于此抽象之上进行:不论是初始化、调用这些基于 rat 数据抽象的过程都是如此,复合数据背后的实现:cons、car、cdr 均不可见。
这一思想的第一个优点就是提升了程序的模块性,使得程序容易维护和修改,比如将有理数约化到最简形式的工作可以在 make-rat 时进行,也可以推迟到实际获取 number 和 denom 时进行。不论怎么设计或者后续需要调整,数据抽象方法带来的模块化能力都能为我们提供便利,且不对系统其它部分的工作造成影响。
;抽象数据的构造函数和选择函数
(define (make-rat n d)
(define (gcd x y)
(if (= y 0) x (gcd y (remainder x y))))
(cond ((or (and (< n 0) (< d 0)) ;双负得正
(and (> n 0) (< d 0))) ;母负转子负 这个桥梁一般在初始化此抽象数据、定义底层交互时使用,比如这里为 rat 数据抽象定义的 add, sub, mul, div, equal运算符。而之后的过程,则完全基于此抽象之上进行:不论是初始化、调用这些基于 rat 数据抽象的过程都是如此,复合数据背后的实现:cons、car、cdr 均不可见。
(make-rat (- n) (- d)))
(else (let ((g (gcd n d)))
(cons (/ n g) (/ d g))))))
(define (number x) (car x))
(define (denom x) (cdr x))
;基于抽象数据的过程定义
(define (add-rat x y)
(make-rat (+ (* (number x) (denom y))
(* (number y) (denom x)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (number x) (denom y))
(* (number y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (number x) (number y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (number x) (denom y))
(* (denom x) (number y))))
(define (equal-rat? x y)
(= (* (number x) (denom y))
(* (number y) (denom x))))
(define (printr x)
(printf "~d/~d\n" (number x) (denom x)))
;基于抽象数据的过程
(define one-half (make-rat 1 2))
(define one-third (make-rat 1 3))
(printr one-half)
(printr one-third)
(printr (add-rat one-half one-third))
(printr (mul-rat one-half one-half))
但更为关键的,数据抽象方法还通过“层层的抽象数据并仅使用与其关联层的抽象”提升了程序设计语言的表达能力:比如下面基于 point 抽象的 segment 抽象,以及更高层次的 rect 抽象。注意实际问题:计算 rect 的周长和面积是如何建立在一层层的数据抽象之上的,并且最终调用的过程是如何实现和大部分不需要关心的过程解耦合的:
(define (make-point x y) (cons x y))
(define (x-point p) (car p))
(define (y-point p) (cdr p))
(define (printp p) (printf "(~d,~d)" (x-point p) (y-point p)))
(define (make-segment x y) (cons x y))
(define (start-segment s) (car s))
(define (end-segment s) (cdr s))
(define (prints s) (printf "[~s,~s]"
(printp (start-segment s))
(printp (end-segment s))))
(define (midpoint-segment s)
(let ((ss (start-segment s))
(se (end-segment s)))
(let ((ssx (x-point ss))
(ssy (y-point ss))
(sex (x-point se))
(sey (y-point se)))
(make-point
(/ (+ ssx sex) 2)
(/ (+ ssy sey) 2)))))
(printp (midpoint-segment (make-segment
(make-point 10 20) (make-point 30 40))))
一个小小的例子:求线段的中点,这里利用了 segment 抽象以及其下的 point 抽象甚至到数值的地步:这里将底层关于点 x 和 y 的基本数据结构被暴露出来了,这意味着 midpoint-segment 是作为一个位于 point 和 segment 的抽象层次内的内部过程,并不是作为依赖 segment 抽象的外部应用而存在的。
(define (make-rect s1 s2) (cons s1 s2))
(define (h-length r) (define s (car r))
(- (x-point (end-segment s)) (x-point (start-segment s))))
(define (v-length r) (define s (cdr r))
(- (y-point (start-segment s)) (y-point (end-segment s))))
(define (rect-length r)
(* 2 (+ (h-length r) (v-length r))))
(define (rect-area r)
(* (h-length r) (v-length r)))
;重新基于对角 point 实现 rect,应用 rect-length 和 rect-area 完全无需更改即可工作
(define (make-rect p1 p2) (cons p1 p2))
(define (h-length r) (define p1 (car r)) (define p2 (cdr r))
(- (x-point p2) (x-point p1)))
(define (v-length r) (define p1 (car r)) (define p2 (cdr r))
(- (y-point p1) (y-point p2)))
基于“数据抽象”带来的这种模块化和模块依赖的数据层次,我们有理由相信,cons,car 和 cdr 也完全可以建立在一个模块中,只要其能正确实现暴露的抽象:car 从 cons 获取第一个,cdr 从 cons 获取第二个值即可,而至于此模块如何实现,则无关紧要。cons-car-cdr-1 提供了一种实现方式(实际 Lisp 直接实现了序列而不是这种方式实现的),注意这里我们看到,所谓的数据通过过程和闭包来进行了模拟:
(define (cons-car-cdr-1)
(define (cons x y)
(define (dispatch m)
(cond ((= m 0) x)
((= m 1) y)
(else (error "Argument not 0 or 1" m))))
dispatch)
(define (car z) (z 0))
(define (cdr z) (z 1)) 1)
更有甚者,还能这样写:
(define (cons-car-cdr-2)
(define (cons x y)
(lambda (m) (m x y)))
(define (car z)
(z (lambda (p q) p))) ;((lambda (m) (m x y)) (lambda (p q) p))
(define (cdr z)
(z (lambda (p q) q)))
(newline))
(define (cons-car-cdr-3)
(define (pow a x)
(cond ((= x 0) 1)
((= x 1) a)
(else (* a (pow a (- x 1))))))
(define (loop number)
(lambda (target)
(define (inner-loop now sum)
(cond ((= (remainder now number) 0)
(inner-loop (/ now number) (+ sum 1)))
(else sum)))
(inner-loop target 0)))
(define (cons a b) (* (pow 2 a) (pow 3 b)))
(define (car x) ((loop 2) x))
(define (cdr x) ((loop 3) x))
(printf "cons(5,10) is ~d, car is ~d, cdr is ~d\n"
(cons 5 10) (car (cons 5 10)) (cdr (cons 5 10))))
上面几个例子中,我们通过过程实现了数据的存储和获取:数据完全可以作为过程产生的“闭包”,而获取数据则通过调用过程来进行。这意味着,我们可以生活在一个完全没有数据的语言中,仅通过对过程进行操作(仅限正整数)来完成计算:Alonzo Church 计数就是这样一种表示形式,此人亦发明了 λ 演算。
(define zero (lambda (f) (lambda (x) x)))
(define (add-1 n)
(lambda (f)
(lambda (x)
(f ((n f) x)))))
;通过代入演算很容易得出 1 2 3 的表示形式
(define one (lambda (f) (lambda (x) (f x))))
(define two (lambda (f) (lambda (x) (f (f x)))))
(define three (lambda (f) (lambda (x) (f (f (f x))))))
;要实现这个过程并不难,只需要将 a 和 b 通过 add-1 的方式表示出来即可
(define (add a b)
(lambda (a)
(lambda (b)
(lambda (f)
(lambda (x)
((a f) ((b f) x)))))))
层次性数据和闭包
了解 JavaScript 的开发者可能很清楚“闭包”一词的含义,这在某种程度上来源于 JavaScript 作者本来是想写 Scheme 编译期的历史。总的来说,闭包一词来自于 Lisp,其包含两层含义:①抽象代数中,如果在某个运算下封闭的一集元素应用此运算本身,其产出仍然是该集合里的元素。②表示一种带有自由变量的过程而用的实现技术。在本文中的闭包指的是第一层含义(原始含义)。
序对这个数据组织模式在很多编程语言中都有对应,Python 或 Go 的元组,Java 和 Scala 的 Tuple,但是大部分语言都没有基于此组织模式进一步深入:在 Go 中元组多用于为过程提供错误信息,在 Java 和 Scala 中,受限于静态类型,用途和 Go 的类似。在 Lisp 中,序对的每个元素都可以是一个值或者一个指针:指向另外一个序对,这种组织模式非常灵活,如下所示:
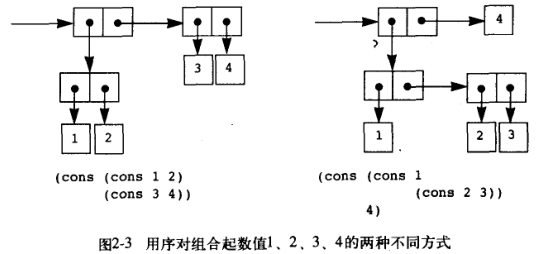
将这种用来根据序对建立元素的能力称之为 cons 的闭包性质:即通过 cons 组合的数据对象的结果本身还可通过同样的操作再进行组合(如果 cons 某个元素为值则不可,为嵌套 cons 则可以)。
表的抽象
这种层次性的结构的灵活性可能超出了我们的想象,比如我们可以用来建立一批数据有序的汇集:序列 List,其相当于 (cons 1 (cons 2 (cons 3 (cons 4 nil)))),可以使用语法糖 (list 1 2 3 4) 来表示,将这个序对的序列称之为一个表。nil,是 nihil 的拉丁语缩写,指的是空,可以将其看做一个不包含任何元素的序列用作表的结束(Chez Scheme 实现中 nil 使用 '() 表示)。注意 Lisp “过程即数据”这一特性表现在:Lisp 的语法 (+ 1 2 3 4) 等本身就是一个表,注意(list 1 2 3 4) 和 (1 2 3 4) 的区别,后者是前者表达式求值的结果,如果后者表示一个表达式,则其会调用 1 这个过程去计算表达式的值,就会出错。
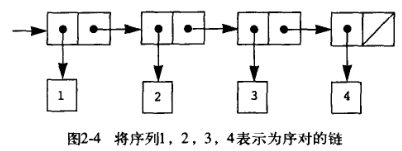
可以很方便的通过 car 和 cdr 从 list 中获取头部元素和去除头部元素,可以通过 cons 将一个 cons 添加一个头部元素。
(define a (list 1 2 3 4));1 2 3 4
(define first-a (car a));1
(define no-head-a (cdr a));2 3 4
(define b (cons "hello" no-head-a)) ;hello 2 3 4
这种表在大部分语言中都有对应实现:比如 Scala 的 List(Python 的 List 本质是一个可扩容 Array,不是表,Java 的 ArrayList 也是一种可扩容 Array,不是表)或者 Java 基于对象实现的 Node 链表,C 基于 struct 实现的链表。这些结构的链表如果要实现数据抽象,就必须使用类型参数,比如
List[Int], List[String]。而对于 C,则缺乏这种复用能力,必须手动指定指针为某个定义好形式的元素。对于动态语言来说数据抽象要好一些,比如 Lisp 和 Python。相比较其他语言基本数据结构 Array 而言,Lisp 的表或者说 List 是一种优缺点鲜明的数据结构:遍历速度很快,插入删除非常灵活和方便,但是占用空间大,查找也很慢。
下面是基于基于序对的表的一些基本操作,基本就是通过在递归/迭代中操作 car 和 cdr,通过 null? 判断来实现的精巧过程,包括获取特定下标项、获取表长度、表组合、获取最后表、表反转等操作。注意,需要深刻认识表的序对构成:序对组成的表第一项始终是值,reverse-err 在递归时虽然在每一层都获取了表的下一个元素,但返回时却无法满足表格式:无法构造表的第二个元素(下一张表),而如果修改实现 reverse-err2,递归也只能返回一样顺序的表(其实递归是可以实现 reverse 的,只需要利用 append 将新元素包装一个 list 并和累加 list 拼接即可,但效率很低,参见此处)。此外要注意表的操作特征类似于栈,因此为实现表反向可以很简单的对迭代对新栈压入,要实现过滤则需要使用递归,每次修改头部元素后,使用 cons 配合下一个元素的递归操作并重新构造新的表。
(define (item lists n)
(if (= n 0) (car lists) (item (cdr lists) (- n 1))))
(define (size lists)
(if (null? lists) 0 (+ 1 (size (cdr lists)))))
(define (append list1 list2)
(if (null? list1) list2 (cons (car list1) (append (cdr list1) list2))))
(define (last-pair lists)
(define (inner first next)
(if (null? next) (cons first '()) (inner (car next) (cdr next))))
(cond ((null? lists) lists)
((null? (cdr lists)) lists)
(else (inner (car lists) (cdr lists)))))
(define (reverse-err lists)
(if (null? (cdr lists))
(car lists)
(cons (reverse-err (cdr lists)) (car lists))))
(define (reverse-err-2 lists)
(if (null? lists)
'()
(cons (car lists) (reverse-err-2 (cdr lists)))))
(define (reverse lists)
(define (inner remain new)
(if (null? remain) new (inner (cdr remain) (cons (car remain) new))))
(inner lists '()))
可以利用表让之前的 cc 换零钱方式更加贴合实际:能为不同国家硬币换零钱 —— 通过定义列表。这里 cc 的实现完全可以让定义的硬币顺序先排序,然后 first-denomination 返回 car cv,except-first-denomination 返回 cdr cv,但这对输入提出了要求。另一种方法就是实现列表的排序,或者按照这里的方法:first-denomination 找出列表最大项,except-first-denomination 先找出最大项,然后构造返回排除这个最大项的新列表。
(define us-coins (list 50 25 10 5 1))
(define uk-coins (list 100 50 20 10 5 2 1 0.5))
(define cn-coins (list 100 50 20 10 5 1))
(define (cc amount coin-values)
(define (no-more? cv) (null? cv))
;基于递归实现(结果反向)
(define (except-first-denomination cv)
(define exclude (first-denomination cv))
(define (inner check collect)
(if (null? check)
collect
(let ((now-check (car check)))
(if (= exclude now-check)
(inner (cdr check) collect)
(inner (cdr check) (cons now-check collect))))))
(inner cv '()))
;基于迭代实现
(define (except-first-denomination cv)
(define exclude (first-denomination cv))
(define (inner check)
(if (null? check) '()
(let ((now-check (car check)))
(if (= exclude now-check)
(inner (cdr check))
(cons now-check (inner (cdr check)))))))
(inner cv))
(define (first-denomination cv)
(let ((now (car cv)))
(if (null? (cdr cv))
now
(if (> now (first-denomination (cdr cv)))
now
(first-denomination (cdr cv))))))
(cond ((= amount 0) 1)
((or (< amount 0) (no-more? coin-values)) 0)
(else
(+ (cc amount
(except-first-denomination coin-values))
(cc (- amount
(first-denomination coin-values))
coin-values)))))
(printf "cc 100 for cn ~d\n" (cc 100 cn-coins))
Scheme 支持可变参数,即将多个连续参数收集到一张表中,使用 x . y 记号,这样传入 1 2 3 4 则 x 为 1,(2 3 4) 为 y。下面是一个基于可变参数实现的过滤和第一个参数相同奇偶性的列表的例子(注意迭代实现得到的结果是反向的,递归实现得到的则是正向的 —— 但这里是树状递归,性能也不一定比迭代 + 反向来得好)。
(define (same-parity check . others)
(define filter
(if (= (remainder check 2) 0)
(lambda (x) (= (remainder x 2) 0))
(lambda (x) (not (= (remainder x 2) 0)))))
(define (loop now new)
(if (null? now)
new
(let ((now-h (car now)))
(if (filter now-h)
(loop (cdr now) (cons now-h new))
(loop (cdr now) new)))))
(loop (reverse (cons check others)) '()))
(define (same-parity-2 check . others)
(define filter
(if (= (remainder check 2) 0)
(lambda (x) (= (remainder x 2) 0))
(lambda (x) (not (= (remainder x 2) 0)))))
(define (loop now)
(if (null? now) '()
(let ((now-h (car now)))
(if (filter now-h)
(cons now-h (loop (cdr now)))
(loop (cdr now))))))
(loop (cons check others)))
(printf "~s\n~s\n" (same-parity-2 1 2 3 4 5 6 7) (same-parity-2 2 3 4 5 6 7))
如果说分数以及调用分数进行计算的过程构成了数据抽象和隔绝底层数据值的抽象屏障,那么对于表而言,上述 length,items,append,reverse 则对于表的实现:car 和 cdr 调用,nil 判定进行了隔离,构建了基于表的数据抽象和抽象屏障。自然,抽象屏障作为数据抽象的生态,如果提供的功能过少,则开发者将不得不深入底层实现,这破坏了数据抽象的封装。而 map 和 for-each 的实现,进一步完善了表的抽象屏障,正如同我们在大部分编程语言中见到的那样(几乎所有编程语言都有列表数据类的 for-each 操作,不论是语法形式上还是函数形式上,大部分语言也有函数形式上的 map 和 flatMap 操作)。
(define (map proc items)
(if (null? items) '()
(cons (proc (car items))
(map proc (cdr items)))))
(printf "~s\n" (map (lambda (x) (* x x)) (list 1 2 3 4 5)))
可以看到,map 是表数据抽象的很好的护城河:其模式足够常见,基于 map 的过程页非常简单且容易理解
(define (square-list items)
(if (null? items) '()
(cons (* (car items) (car items))
(square-list (cdr items)))))
(define (square-list-2 items) (map (lambda (x) (* x x)) items))
此外,for-each 甚至可以基于 map 实现,或者可以和 map 平级,基于对表底层操作实现
(define (for-each proc items) (map proc items) '())
(for-each (lambda (x) (newline) (display x))
(list 57 321 88))
下面是一个例子,其可以返回一个列表的所有子集的表,比如 (1 2 3) 返回 (() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3)) 这个表,其实现异常的简单优雅:这个问题等同于返回除了第一个元素其余的元素组成的表 + 第一个元素和此表所有元素合并的元素,后者只需要一个 map 然后为每个后续表的元素 cons 合并此元素即可:
(define (subsets s)
(if (null? s) (list '())
(let ((rest (subsets (cdr s))))
(append rest (map (lambda (x) (cons (car s) x)) rest)))))
(printf "~s\n" (subsets (list 1 2 3)))
树的抽象
表只是序对的一种特殊组织形式,如果使用序对组合多张表,比如 (cons (list 1 2) (list 3 4)),那么其本质就是 (cons (cons 1 (cons 2)) (cons 3 (cons 4)))。如果说 cons 适合使用链条表示,那么 lists 更适合使用树来表示。右上图为 (cons (list 1 2) (list 3 4)) 的树,右下图为 (list 1 (list 2 (list 3 4))) 的树,可以观察到:每个 list 字面量是一个分支节点,每个值是一个叶子。
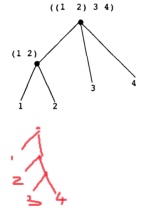
注意区分 (1 2) 这样的表字面量、(list 1 2) 这样的表表达式、(cons 1 2) 这样的序对之间的区别,这里最容易混淆的就是 (1 2) 这样的结构并不是 (cons 1 2) 的简写,而是 (cons 1 (cons 2 nil)) 的简写。
(define c (list 1 (list 2 (list 3 (list 4 (list 5 (list 6 7)))))))
(printf "~s\n" ;for 7
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr c)))))))))))))
(define c2 '(1 (2 (3 (4 (5 (6 7)))))))
(printf "~s\n" ;for 7
(car (cdr (car (cdr (car (cdr (car (cdr (car (cdr (car (cdr c2)))))))))))))
(define c3 (cons 1 (cons 2 (cons 3 (cons 4 (cons 5 (cons 6 7)))))))
(printf "~s\n" (cdr (cdr (cdr (cdr (cdr (cdr c3)))))))
如果说“序对”为结合提供了基础条件,那么“表”这种特殊的序对结构则让大规模数据结合成为可能(注意对于 list 而言,car 获取首个元素,cadr 获取余下元素,其相当于 cdr 后进行 car,见下图),而“序对结合的表”这种结构则为层次性数据结构提供了必要的支持。注意,基于 cons 组合的层次结构可作为二叉树,但仅此而已,混合 cons 和 list 带来的灵活性也不高,而完全基于 list 组合的层次结构可在每一层无限扩充,灵活性更高,后面的“树”指的主要是基于 list 表实现的层次数据结构,如下图所示。
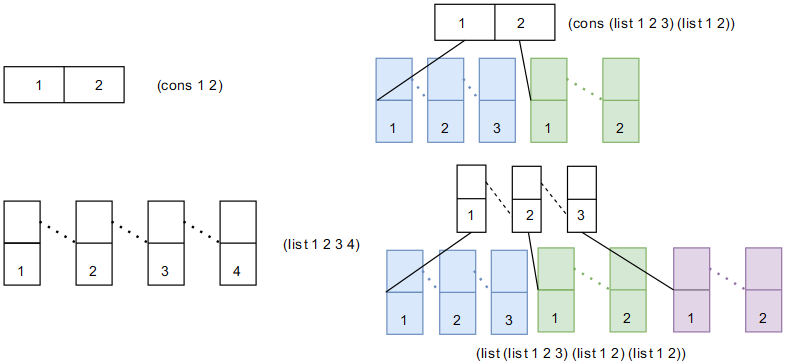
上述对表的 length 现在不能用于树:表仅将第一个序对元素看做值。定义 count-leaves 过程,让其统计树叶的值,为实现这个方法,需要依赖 Scheme 的 pair? 过程检测序对每一个元素,然后递归的对左树和右树进行统计(其实就是二叉树的遍历):
(define (count-leaves x) ;count leaves for tree
(cond ((null? x) 0) ;end-point
((not (pair? x)) 1) ;leaf
(else (+ (count-leaves (car x)) ;node-head
(count-leaves (cdr x)))))) ;node-tail
(printf "~d\n" (count-leaves (list (list 1 2) 3 4)))
而 reverse 过程也需要对树进行重写:区别于针对表的 reverse 只能对第一层的序对反转,deep-reverse 可以对树的每层序对的每个表进行反转。:
(define (deep-reverse items)
(cond ((null? items) '())
((not (pair? items)) items) ;for list, cadr to get rest
(else (reverse (list (deep-reverse (car items))
(deep-reverse (cadr items)))))))
(printf "~s\n" (deep-reverse '((1 2) (3 4))))
此外,我们可能需要一个返回树的叶子(从左到右)的方法,将其称之为 fringe。注意,树的过程可基于表的抽象来实现,而不用深入 cons, car 和 cdr, cadr —— 虽然有时候这是不得不的。fringe 方法是一个绝佳的例子:基于表的 append 方法,而非基于序对:
(define (fringe tree)
(cond ((null? tree) '())
((not (pair? tree)) (list tree))
(else (append (fringe (car tree)) (fringe (cadr tree))))))
(define x '((1 2) (3 4)))
(printf "~s ~s\n" (fringe x) (fringe (list x x)))
实际上,不论是基于 cons, car 和 cdr 抽象的 list,还是基于 list, car, cadr 抽象的 tree,我们始终在基于某个更易思考和操作数据概念平面上活动。这种数据平面可以是抽象的 list 和 tree,也可以是和问题密切相关的:下面展示了一个基于 list 抽象的结构,这种结构包含活动体 mobile,活动体由两个分支 branch 构成,每个分支具有长度和负载,负载可以是一个重物或者是一个活动体。我们通过构造函数 make-mobile 和 make-branch 以及解析函数 left-branch 与 right-branch,branch-length 与 branch-structure,然后基于这些数据抽象实现计算总活动体重量(每个分支下重物的重量之和)total-weight,计算活动体是否平衡(左边分支力矩等于右边分支力矩,且左右分支下的每个活动体都保持平衡)is-balance(注意平衡其实可以复用分支总重量的代码),这个例子想要展现的是“基于业务实施进行的数据抽象”以及基于这种抽象大厦表示的复杂思维过程,以及这种过程是如何做到和数据抽象层以下的实现无关的:构造函数和解析函数很容易替换为其他实现,比如 cons, car 和 cdr 而不是 list, car 与 cadr,甚至利用之前学到的,继续更换默认 cons,car 和 cdr 的系统实现,通过过程闭包实现 cons,car 和 cdr。
#| (define (make-mobile left right) (list left right))
(define (make-branch length structure) (list length structure))
(define (left-branch mobile) (car mobile))
(define (right-branch mobile) (cadr mobile))
(define (branch-length branch) (car branch))
(define (branch-structure branch) (cadr branch)) |#
(define (make-mobile left right) (cons left right))
(define (make-branch length structure) (cons length structure))
(define (left-branch mobile) (car mobile))
(define (right-branch mobile) (cdr mobile))
(define (branch-length branch) (car branch))
(define (branch-structure branch) (cdr branch))
(define (total-weight mobile)
(define (bw branch)
;分支重量等于:如果分支挂着重物,则是重物重量
;如果分支作为一个活动体,则返回子活动体重量
(if (pair? (branch-structure branch))
(aw (branch-structure branch))
(branch-structure branch)))
(define (aw mobile)
;活动体重量等于左边分支重量 + 右边分支重量
(+ (bw (left-branch mobile)) (bw (right-branch mobile))))
(aw mobile))
(define (is-balance mobile)
;对于节点,平衡意味着左侧分支和右侧分支力矩相等且分支均平衡
(define (mobile-balance? mobile)
(let ((left (left-branch mobile))
(right (right-branch mobile)))
(and (same-weight? left right)
(branch-balance? left)
(branch-balance? right))))
(define (branch-balance? branch)
;对于分支,如果仅挂重物,则平衡,反之判断挂载节点是否平衡
(let ((bs (branch-structure branch)))
(if (pair? bs) (mobile-balance? bs) #t)))
(define (same-weight? left right)
;左右两侧力矩是否相等:长度 * 重量,重量递归计算
(define (branch-weight branch)
(if (pair? (branch-structure branch))
(total-weight (branch-structure branch))
(branch-structure branch)))
(define (total-weight mobile)
(+ (branch-weight (left-branch mobile))
(branch-weight (right-branch mobile))))
(= (* (branch-weight left) (branch-length left))
(* (branch-weight right) (branch-length right))))
(mobile-balance? mobile))
(define m1 (make-mobile (make-branch 10 100)
(make-branch 20 200)))
(define balance-mobile (make-mobile (make-branch 10 10)
(make-branch 10 10)))
(define unbalance-mobile (make-mobile (make-branch 10 balance-mobile)
(make-branch 10 200)))
(printf "mobile weight:~d\n" (total-weight m1))
(printf "is b-m balanced? ~s\n" (is-balance balance-mobile))
(printf "is ub-m balanced? ~s\n" (is-balance unbalance-mobile))
同样的,tree 也可以有 tree-map 来简化对每个元素应用的操作。注意这里的 tree 并不适用于非 tree 结构的 cons/list,其始终会得到 ():
(define (tree-map tree action)
(cond ((null? tree) '())
((not (pair? tree)) (action tree))
(else (cons (tree-map (car tree) action)
(tree-map (cdr tree) action)))))
(define (square-tree tree)
(cond ((null? tree) '())
((not (pair? tree)) (* tree tree))
(else (cons (square-tree (car tree)) (square-tree (cdr tree))))))
(define (square-tree-2 tree) (tree-map tree (lambda (x) (* x x))))
(printf "~s ~s\n"
(square-tree '(1 (2 (3 4) 5) (6 7)))
(square-tree-2 '(1 (2 (3 4) 5) (6 7))))
(序列)作为一种约定的界面
在序对,表和数这些数据抽象中,表(序列)是最适合大部分应用场景的一种抽象。在大部分编程语言中,作为数据结构的序列也总是该语言的基础和核心。上面我们介绍了围绕序列这个数据抽象提供的一系列过程生态,比如 filter, map, length, append 等。使用这些生态在解决实际问题的过程中,我们会发现:在序列这个数据抽象的众多过程中,总有一些能提供适合更多应用的过程抽象,如果有,我们认为可能是如下三个:filter、map (包括 flat-map) 和 fold(包括 fold-left, fold-right, accumulate),其中 filter 和 fold 是必不可少的(这里的 fold 本质是 fold-right,其含义为,对 seq 的每个元素,递归应用和 init 这个状态值的 op 操作,之所以说是 fold-right,是因为这是使用递归实现的,因此知道 seq 遍历到最后一个元素,才开始应用和 init 的 op 操作,即逆序的):
(define (filter pre seq)
(cond ((null? seq) '())
((pre (car seq))
(cons (car seq) (filter pre (cdr seq))))
(else (filter pre (cdr seq)))))
(define (fold op init seq)
(if (null? seq) init (op (car seq) (fold op init (cdr seq)))))
fold 能够拓宽序列这一数据抽象的应用范围,下面是一些例子,比如计算一棵树的奇数的平方和 sum-odd-squares,计算从 0 到 n 的计数斐波契些数 even-fibs,计算从 0 到 n 的斐波那契数平方,计算一个序列偶数的平方的乘积,计算公司程序员的最高收入。说实话,如果没有 fold 这个过程抽象,这些应用的实现过程将看起来千差万别,凭谁第一眼看上去也不会觉得能有一个共同的模板出来。fold 的本质在于:它提供了一种对序列每个元素按照某个过程进行整合的抽象,这种抽象对序列和整合没有任何假设,只要求序列可逐个迭代提供值,直到结束,整合可操作某个内存位置的变量,仅此而已。
(define (demo-of-data-abstraction)
(define odd? (lambda (x) (= (remainder x 2) 0)))
(define even? (lambda (x) (not (= (remainder x 2) 0))))
(define square (lambda (x) (* x x)))
(define (enumerate-interval low high)
(if (> low high) '()
(cons low (enumerate-interval (+ low 1) high))))
(define (fib n)
(define (iter a b count)
(if (= count 0) b (iter (+ a b) a (- count 1))))
(iter 1 0 n))
(define (sum-odd-squares tree)
(fold + 0 (map square (filter odd? (fringe tree)))))
(define (even-fibs n)
(fold cons '() (filter even? (map fib (enumerate-interval 0 n)))))
(define (list-fib-squares n)
(fold cons '() (map square (map fib (enumerate-interval 0 n)))))
(define (product-of-square-of-odd-elements seq)
(fold * 1 (map square (filter odd? seq))))
(define (salary-of-highest-paid-programmer people-list)
(define programmer? ???)
(define salary ???)
(fold max 0 (map salary (filter programmer? people-list)))) '())
fold 充分展现出了抽象之美,可以使用它来实现 map, append, length 这些过程,可以看到,map 无非是 fold 对每个遍历元素应用外部操作并进行 cons 重新整合,append 无非是 fold 对于一个序列进行遍历并通过 cons 整合到另一个序列,length 无非是对一个序列进行遍历并对 0 开始累加。
(define (map p seq)
(fold (lambda (x y) (cons (p x) y)) '() seq))
(define (append seq1 seq2)
(fold cons seq2 seq1))
(define (length seq)
(fold (lambda (x y) (+ y 1)) 0 seq))
fold 的功能不仅如此,它还可以直接应用到多个问题解决上,比如用 horner 方法计算多项式函数结果,基于 length 来统计树的叶子个数。
(define (horner-eval x coeff-seq)
;计算多项式函数结果,coeff-seq 为从低到高项的因子
(fold (lambda (this-coeff higher-terms)
(+ this-coeff (* higher-terms x))) 0 coeff-seq))
(printf "~s\n" (horner-eval 2 '(1 3 0 5 0 1)))
(define (count-leaves tree)
(define len (lambda (x) (if (not (pair? x)) 1 (length x))))
(fold + 0 (map len tree)))
(printf "~s\n" (count-leaves '((1 2) 3 4)))
最后,fold 还可以继续增强抽象能力,fold-n 是一个用来对嵌套序列的每个元素位置进行 fold 并最后返回一个等长序列结果的过程。
(define (fold-n op init seqs)
;seqs 是一个嵌套的序列,其返回一个和 seqs 等长的序列,其中每一项都是
;seqs 每个子序列特定位置的 fold 结果
(if (null? (car seqs)) '()
(cons (fold op init (map car seqs))
(fold-n op init (map cdr seqs)))))
(printf "~s\n" (fold-n + 0 '((1 2 3)(4 5 6)(7 8 9)(10 11 12))))
基于 fold 和 fold-n 提供的对于序列的数据抽象和过程抽象,我们可以将其作为一个平台,其上封装业务相关的新的数据抽象和过程抽象,比如用来实现矩阵的数据抽象以进行矩阵计算,这个例子非常巧妙,dot-product 点乘,matrix-vector 矢量矩阵乘法,transpose 转秩, matrix-matrix 矩阵乘法这些基于矩阵数据抽象的生态过程基于序列提供的强大的过程抽象过程轻轻松松就实现了。这里试图说明的问题是,软件开发生态为王,封装一个数据抽象不难,但要想实现“将其作为一种约定的界面”,则必须基于此数据抽象提供丰富的、合适层级的过程抽象,比如列表提供的 filter,map,flatmap 和 fold 才能够建立合用的生态,以吸引开发者基于此抽象进行开发。
;假设 ((1 2 3 4)(4 5 6 6)(6 7 8 9)) 是矩阵每行/列的表示,那么通过 map, fold 以及
;fold-n 可建立 dot-product, matrix-vector, transpose, matrix-matrix 的抽象
(define (dot-product v w)
(fold + 0 (map * v w)))
(define (matrix-*-vector m v)
(map (lambda (items) (dot-product items v)) m))
(define (transpose mat)
(fold-n cons '() mat))
(define (matrix-*-matrix m n)
(let ((n-cols (transpose n)))
(map (lambda (m-col) (matrix-*-vector n-cols m-col)) m)))
注意,上述介绍的 fold 本质是 fold-right(基于递归,最后一个元素先和 init 执行 op),而基于迭代的 fold-left 也不难实现:
(define (fold-left op init seq)
(define (iter result rest)
(if (null? rest) result
(iter (op result (car rest)) (cdr rest))))
(iter init seq))
(define (fold-right op init seq)
(if (null? seq) init
(op (car seq) (fold-right op init (cdr seq)))))
这两种实现 fold-left 和 fold-right 并不能对一样的 op 和 init,seq 得到相同的结果,除非 op 满足交换律,比如 + * 之类,而不能是 / 和 -。最后,在前面的例子中,我们提到序列 reverse 可以简单地通过迭代 cons 当做栈插入到新的序列头来实现,在这里 reverse-by-left 使用 fold-left 重现了这一过程:init 作为新的序列,cons 作为 op。当时没有提到的是,如果使用递归当如何做,这里也提供了基于 reverse-by-right 使用 fold-right 的实现,只需要很简单的利用列表的 append 方法将其插入到新的序列尾部即可,当然,这种方法的效率相比较 reverse-by-left 差的不是一星半点,因此,在大部分支持列表数据抽象的语言中,往往会同时提供 foldLeft 和 foldRight 函数(比如 Scala)。
(define (reverse-by-left seq)
(fold-left (lambda (ele acc) (cons acc ele)) '() seq))
(define (reverse-by-right seq)
(fold-right (lambda (ele acc) (append acc (list ele))) '() seq))
(printf "~s\n" (reverse-by-left '(1 2 3 4 5)))
(printf "~s\n" (reverse-by-right '(1 2 3 4 5)))
不论是在 Scala, Java 还是 JavaScript 中,flatmap 都是一个非常神秘的过程,它好像有什么超能力一般,能将 List[List[String]] 给拍平成 List[String]。但其实,其实现可以非常简单,可以定义为一种先 map 后 fold 结果到一个 list 中的过程抽象。flatmap 可用于类似于 C/Java 的嵌套 for 循环场景中,每个外层循环值对应的内层循环遍历后得到的序列(map 过程)在外层循环中进行整合(fold 过程),因此,foldmap 的 procedure 通常定义为内层循环产生序列的匿名过程,其可以依赖外层循环每次提供的外部序列的单个元素。比如下面的 prime-sum-pairs 就是产生 0 - n 之间的两个数之和为素数的所有情况,为完成这个目标,先得到所有 0 - n 的数以及其和组成的序列,然后进行 prime? filter 最后表示为目标格式 map。而得到这个序列则依赖于嵌套的 for 循环,在 Lisp 中就是对一个 Range map(外层),然后在每次 map 的时候,对另一个 Range map(内层)并生成序对,内层 Range 依赖于外部 Range map 时提供的元素值,但这种嵌套 map 得到的结果是 List[List[Pair]],需要使用 fold 拍平装在一个 list 中,换言之,应该是一个 flatmap 嵌套内层 map。
(define (flatmap proc seq) (fold append '() (map proc seq)))
(define (prime-sum-pairs n)
(map (lambda (pair)
(list (car pair) (cadr pair)
(+ (car pair) (cadr pair))))
(filter (lambda (pair)
(prime? (+ (car pair) (cadr pair))))
(flatmap (lambda (i)
(map (lambda (j) (list i j))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))))
(printf "~s\n" (prime-sum-pairs 10))
prime-sum-pair 的另一种实现方式是先生成更精简的数对(因为 1 + 3 和 3 + 1 在上述过程中是重复的,内层循环的 j 不必大于 i 即可):unique-pairs 实现了这一过程,prime-sum-pairs 则基于此过程抽象进行了素数过滤和展示。
(define (unique-pairs n)
(flatmap (lambda (i) (map (lambda (j) (list i j))
(enumerate-interval 1 (- i 1))))
(enumerate-interval 1 n)))
(define (prime-sum-pairs n)
(map (lambda (pair) (list (car pair)
(cadr pair)
(+ (car pair) (cadr pair))))
(filter (lambda (pair)
(prime? (+ (car pair) (cadr pair))))
(unique-pairs n))))
这种嵌套映射的模式是 flatmap 的主要应用场景,注意内层 map 的数据来源并不一定是一个范围(就像嵌套 for 循环那样),也有可能是来自自身的递归调用,只要能够生成序列应用 map 即可,下面的 permutations 实现了集合 s 的所有可能排列:思想很简单:某个元素和排除这个元素的 permutations 集合所有元素进行组合就是问题的答案,很显然,需要对每个元素都应用这一过程,然后将结果合并,因此使用 flatmap。
(define (permutations s)
;生成集合 s 的所有可能排列
;去除某个元素后的集合的所有可能排列加上当前元素, 然后整合起来
(define (remove x s) (filter (lambda (e) (not (= e x))) s))
(if (null? s) (list '())
(flatmap (lambda (x)
(map (lambda (p) (cons x p))
(permutations (remove x s))))
s)))
(printf "~s\n" (permutations '(1 2 3)))
下面这个例子展示了 flatmap 嵌套 flatmap 嵌套 map 的“嵌套映射”,用来解决三个小于 n 的有序数和为 s 的问题,这里的迭代类似于 C 中的三层 for 循环。
(define (sum-of-3-number-smaller-than-n-equal-s n s)
(filter (lambda (tuple)
(let ((a (car tuple))
(b (cadr tuple))
(c (cadr (cdr tuple))))
(and (not (= a b))
(not (= b c))
(not (= a c))
(= (+ a b c) s))))
(flatmap (lambda (a)
(flatmap (lambda (b)
(map (lambda (c) (list a b c))
(enumerate-interval 1 n)))
(enumerate-interval 1 n)))
(enumerate-interval 1 n))))
(printf "SUM:\n~s\n" (sum-of-3-number-smaller-than-n-equal-s 10 15))
下面这个例子展示了 flatmap 嵌套 map 的“嵌套映射” 以解决八皇后问题,外层是递归(递归每个棋盘除了最右侧列之外棋盘的可能皇后组合),内层是迭代(用来计算在除了最右侧列外其余可能的位置和最右侧列从上到下如果是新皇后是否满足条件的判断:此判断位于 adjoin-position 中,is-ok 执行了判断,如果合适,则将新皇后插入可能的列表头,反之则将 -1 插入列表后,然后在 flatmap 外进行过滤):
(define (queens board-size)
(define (adjoin-position new-row k rest-of-queens)
;计算 k 列 r 行是否可行,如果可以返回 #t 不可以返回 #f
(define (is-ok now-queen-col rest-of-queens)
(if (null? rest-of-queens) #t
(and (let ((now-queen-row (car rest-of-queens)))
(and (not (= new-row ;不能在同行
now-queen-row))
(not (= new-row ;不能在对角线
(+ (- k now-queen-col) now-queen-row)))))
(is-ok (- now-queen-col 1) (cdr rest-of-queens)))))
;(printf "for row ~s in col ~s, exist: ~s\n" new-row k rest-of-queens)
(cond ((null? rest-of-queens) (list new-row))
((is-ok (- k 1) rest-of-queens)
(append (list new-row) rest-of-queens))
(else (list -1 rest-of-queens))))
(define (safe? k positions) ;新皇后是否安全
(if (null? positions) #t (not (= (car positions) -1))))
(define (queen-cols k) ;棋盘在前 k 列放皇后的布局
(if (= k 0)
(list '())
(filter (lambda (positions) (safe? k positions))
(flatmap (lambda (rest-of-queens)
;所有旧皇后的摆放方式
(map (lambda (new-row)
;对于新列的每一行, 计算新皇后可能的位置
(adjoin-position new-row k rest-of-queens))
(enumerate-interval 1 board-size)))
(queen-cols (- k 1))))))
(queen-cols board-size))
(printf "~s\n" (queens 8))
实例:易理解的数据屏障和深刻的过程抽象 —— 打造恰好的分层
下面是一个综合了本章和上一章的例子:一种图形语言。对于任何语言而言,需要关注的核心有三点:基本原语、组合方式和抽象手段。对于这种图形语言,唯一的原语就是 painter,其可以进行一系列的变换,比如上下镜像 below,左右镜像 beside,水平翻转和垂直翻转。
;基础过程:图画右边镜像
(define (beside painter) ???)
;基础过程:图画下面镜像
(define (below painter) ???)
;基础过程:垂直翻转
(define (flip-vert painter) ???)
;基础过程:水平翻转
(define (flip-horiz painter) ???)
基于这些基本过程,我们可以进行组合以实现一些模式:
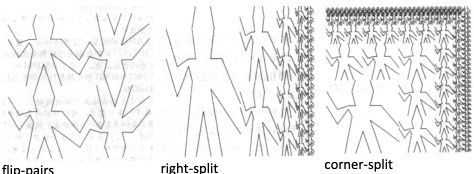
;组合过程:垂直翻转并镜像然后上下加倍
(define (flip-pairs painter)
(let ((painter2 (beside painter (flip-vert painter))))
(below painter2 painter2)))
;组合模式:右侧分裂
(define (right-split painter n)
(if (= n 0) painter
(let ((smaller (right-split painter (- n 1))))
(beside painter (below smaller smaller)))))
;组合模式:顶部分裂
(define (up-split painter n)
(if (= n 0) painter
(let ((smaller (up-split painter (- n 1))))
(below painter (beside smaller smaller)))))
;高级组合模式:右侧分裂,顶部分裂,对角缩小镜像
(define (corner-split painter n)
(if (= n 0) painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1))))
(let ((top-left (beside up up))
(bottom-right (below right right))
(corner (corner-split painter (- n 1))))
(beside (below painter top-left)
(below bottom-right corner))))))
;高级组合模式:将上述 corner-split 水平翻转并和原始左右堆砌,
;组成的新图案垂直翻转并和原始上下堆砌
(define (square-limit painter n)
(let ((quarter (corner-split painter n)))
(let ((half (beside (flip-horiz quarter) quarter)))
(below (flip-vert half) half))))
随着过程越来越多,我们逐渐发现一些模式,可以利用上一章学习的过程抽象以进行提取:
;过程抽象:将四个图形上下左右放置
(define (square-of-four tl tr bl br)
(lambda (painter)
(let ((top (beside (tl painter) (tr painter)))
(bottom (beside (bl painter) (br painter))))
(below bottom top))))
;基于高阶抽象重写的 flipped-pairs
(define (flipped-pairs-2 painter)
(define identity (lambda (x) x))
(let ((c4 (square-of-four
identity flip-vert identity flip-vert)))
(c4 painter)))
;基于高阶抽象重写的 square-limit
(define (square-limit-2 painter n)
(define identity (lambda (x) x))
(define rotate180 (lambda (x) (flip-horiz (flip-vert x))))
(let ((c4 (square-of-four flip-horiz identity
rotate180 flip-vert)))
(c4 (corner-split painter n))))
;同样的,可以对 up-split 和 bottom-split 进行过程抽象
(define (split action1 action2)
(define (inner painter n)
(if (= n 0) painter
(let ((smaller (inner painter (- n 1))))
(action1 painter (action2 smaller smaller)))))
(lambda (painter n) (inner painter n)))
(define right-split-2 (split beside below))
(define up-split-2 (split below beside))
为实现 painter 这个原语,首先需要定义框架,一个框架包含三个向量,包含了零点(基准向量)和两个框架角向量。一般而言,在一个 1 * 1 的正方形中,基准向量为 (0,0),两个角向量分别为 (1,0) 和 (0,1)。对于任意框架,将一个向量(x, y)映射到框架中需要分别执行:OriginX + xEdge1X, OriginY + yEdge2Y。为了实现这个框架,需要建立数据抽象:这里定义了 frame 的数据抽象和一些选择函数,vect 的数据抽象和其选择函数,一些运算过程,最后在 frame-coord-map 中实现了框架映射。
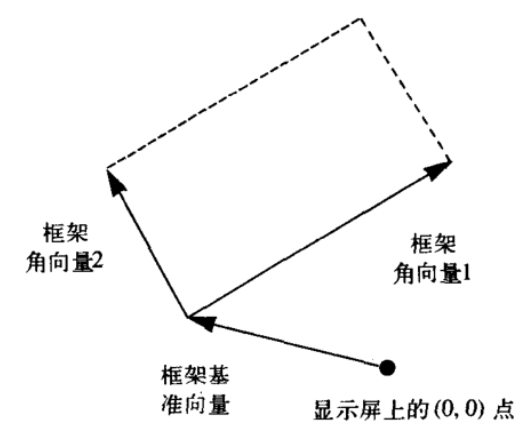
;构建数据抽象:框架数据抽象由一个基准向量和两个角向量构成
; (define (make-frame o e1 e2) (list o e1 e2))
; (define (origin-frame f) (car f))
; (define (edge1-frame f) (cadr f))
; (define (edge2-frame f) (cadr (cdr f)))
(define (make-frame o e1 e2) (cons o (cons e1 e2)))
(define (origin-frame f) (car f))
(define (edge1-frame f) (cadr f))
(define (edge2-frame f) (cdr (cdr f)))
;向量数据抽象及向量的加减缩放运算
(define (make-vect x y) (cons x y))
(define (xcor-vect v) (car v))
(define (ycor-vect v) (cdr v))
(define (add-vect v1 v2)
(make-vect (+ (xcor-vect v1) (xcor-vect v2))
(+ (ycor-vect v1) (ycor-vect v2))))
(define (sub-vect v1 v2)
(make-vect (- (xcor-vect v1) (xcor-vect v2))
(- (ycor-vect v1) (ycor-vect v2))))
(define (scale-vect v s)
(make-vect (* s (xcor-vect v)) (* s (ycor-vect v))))
;为了将某个向量 v 映射到框架 frame,通过 frame-coord-map 进行
;v=(x,y) 到 O + xE1 + yE2 的映射
(define (frame-coord-map frame)
(lambda (v)
(add-vect
(origin-frame frame)
(add-vect (scale-vect (xcor-vect v)
(edge1-frame frame))
(scale-vect (ycor-vect v)
(edge2-frame frame))))))
注意这里数据抽象的实际实现可选择任意方式,cons, list 甚至是基于过程的闭包都可以 —— 这正是数据抽象的意义所在,只有在选择函数中为其提供合适的实现即可。
接下来,我们就可以基于 vect, frame 来继续数据抽象,实现画家 painter 了。假设存在一个系统函数 draw-line,这里利用了之前的 segment 数据抽象表示线段。
;假设操作系统实现了 draw-line
(define (draw-line v1 v2) ???)
;基于向量建立新的数据抽象线段
(define (make-segment v1 v2) (cons v1 v2))
(define (start-segment s) (car s))
(define (end-segment s) (cdr s))
接下来画家的定义,就可以对一个 frame 来调用 draw-line 过程进行实际绘图了,这里依赖传入的 segment-list 即绘制线段。注意,画家这个数据抽象现在使用过程进行的表示,在之前我们也见过这样的例子:基于闭包实现的 cons, car 和 cdr, 甚至基于过程实现的数据。
;画家的一个定义如下,其画 segment-list 笔
;其接受一个 frame,然后对每一笔 segment 先进行坐标映射,
;然后进行绘制。画家是一个很好的“数据”抽象屏障,尽管这里的数据
;实际是使用调用系统 draw-line 的过程表示的
(define (segments->painter segment-list)
(lambda (frame)
(for-each
((lambda (segment)
(draw-line
((frame-coord-map frame) (start-segment segment))
((frame-coord-map frame) (end-segment segment))))
segment-list)))
基于这个 segments->painter 抽象屏障,我们可以实现各式各样的画家,比如绕着边框转的 border-painter,画 x 型的 x-painter,画菱形的 lozenge-painter 以及上图提到的 wave-painter。
(define border-painter
(segments->painter
(list
(make-segment (make-vect 0 0) (make-vect 0 1))
(make-segment (make-vect 0 1) (make-vect 1 1))
(make-segment (make-vect 1 1) (make-vect 1 0))
(make-segment (make-vect 1 0) (make-vect 0 0)))))
(define x-painter
(segments->painter
(list
(make-segment (make-vect 0 0) (make-vect 1 1))
(make-segment (make-vect 0 1) (make-vect 1 0)))))
(define lozenge-painter
(segments->painter
(list
(make-segment (make-vect 0 0.5) (make-vect 0.5 1))
(make-segment (make-vect 0.5 1) (make-vect 1 0.5))
(make-segment (make-vect 1 0.5) (make-vect 0.5 0))
(make-segment (make-vect 0.5 0) (make-vect 0 0.5)))))
(define wave-painter
(segments->painter
(list
(make-segment (make-vect 0 0.8) (make-vect 0.2 0.5))
(make-segment (make-vect 0.2 0.5) (make-vect 0.3 0.6))
(make-segment (make-vect 0.3 0.6) (make-vect 0.2 0.8))
(make-segment (make-vect 0.2 0.8) (make-vect 0.3 1.0))
(make-segment (make-vect 0.7 1.0) (make-vect 0.8 0.8))
(make-segment (make-vect 0.8 0.8) (make-vect 0.7 0.6))
(make-segment (make-vect 0.7 0.6) (make-vect 0.8 0.6))
(make-segment (make-vect 0.8 0.6) (make-vect 1.0 0.3))
(make-segment (make-vect 0.0 0.5) (make-vect 0.2 0.3))
(make-segment (make-vect 0.2 0.3) (make-vect 0.3 0.5))
(make-segment (make-vect 0.3 0.5) (make-vect 0.2 0.0))
(make-segment (make-vect 0.3 0.0) (make-vect 0.5 0.3))
(make-segment (make-vect 0.5 0.0) (make-vect 0.7 0.0))
(make-segment (make-vect 0.8 0.0) (make-vect 0.7 0.5))
(make-segment (make-vect 0.7 0.5) (make-vect 1.0 0.2)))))
至此,我们实现了 painter 这一数据抽象,并且基于此数据抽象实现了众多过程以绘制不同模式,并且在这些过程中抽象出模板(即过程抽象),实现了代码复用,提升了语言表达力。当然,前面提到的画家的变换和组合这里也可以很简单的实现:这里提供了一个 transform-painter 的过程抽象模板,简而言之就是对变换后的 painter 在通过特定 frame 从 frame-coord-map 得到映射关系 m 后,按照闭包 transform-painter 提供的规则对 origin, corner1 和 corner2 分别进行变换以重新映射矢量。下面是基于 transform-painter 的一些示例,可以看到对画家进行变换何其简单:flip-vert 对 painter 进行了反转,shrink-to-upper-right 让 painter 缩放到了右上角四分之一的位置,squash-inwards 则向中间进行收缩。
(define (transform-painter painter origin c1 c2)
(lambda (frame)
(let ((m (frame-coord-map frame)))
(let ((new-origin (m origin)))
(painter
(make-frame new-origin
(sub-vect (m c1) new-origin)
(sub-vect (m c2) new-origin)))))))
(define (flip-vert painter)
(transform-painter painter (make-vect 0.0 1.0)
(make-vect 1.0 1.0) (make-vect 0.0 0.0)))
(define (shrink-to-upper-right painter)
(transform-painter painter (make-vect 0.5 0.5)
(make-vect 1.0 0.5) (make-vect 0.5 1.0)))
(define (rotate90 painter)
(transform-painter painter (make-vect 1.0 0.0)
(make-vect 1.0 1.0) (make-vect 0.0 0.0)))
(define (squash-inwards painter)
(transform-painter painter (make-vect 0.0 0.0)
(make-vect 0.65 0.35) (make-vect 0.35 0.65)))
因此,上述依赖的 beside, below, flip-horiz,rotateX 等 painter 生态过程也就很容易通过这个 transform-painter 进行实现。注意,这里的 below 提供了基于 transfomr-painter 的实现,也提供了基于变换的实现(封装层次更高)。
(define (beside painter1 painter2)
(let ((split-point (make-vect 0.5 0.0)))
(let ((paint-left
(transform-painter painter1
(make-vect 0.0 0.0)
split-point
(make-vect 0.0 1.0)))
(paint-right
(transform-painter painter2
split-point
(make-vect 1.0 0.0)
(make-vect 0.5 1.0))))
(lambda (frame)
(paint-left frame)
(paint-right frame)))))
(define (flip-horiz painter)
(lambda (frame) (transform-painter
painter
(make-vect 1.0 0.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0))))
(define (rotate180 painter)
(lambda (frame) (transform-painter
painter
(make-vect 1.0 1.0)
(make-vect 0.0 1.0)
(make-vect 1.0 0.0))))
(define (rotate270 painter)
(lambda (frame) (transform-painter
painter
(make-vect 1.0 0.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0))))
(define (below painter1 painter2)
(let ((split-point (make-vect 0.0 0.5)))
(let ((paint-top
(transform-painter painter2
split-point
(make-vect 1.0 0.5)
(make-vect 0.0 1.0)))
(paint-bottom
(transform-painter painter1
(make-vect 0.0 0.0)
(make-vect 1.0 0.0)
split-point)))
(lambda (frame)
(paint-top frame)
(paint-bottom frame)))))
(define (below2 painter1 painter2)
(flip-horiz (rotate90
(beside (rotate270 painter1)
(rotate270 painter2)))))
上面这个“图形语言”的例子反映了数据抽象和过程抽象最核心的内容,我们将数据抽象表示为过程,封装了系统底层的 API,基于层层的数据抽象:vect, segment, frame 进行封装,通过 frame-coord-map 和 segments->painter 对 painter 进行了实现,搭建起从系统 API draw-segment 到 painter 的桥梁,并使得基于 painter 打造数据屏障成为可能,而在其上,通过 transform-painter 这一核心的过程抽象实现了一组数据生态过程,比如 below, flip, beside, rotate 等,而在这些生态过程之上又通过 square-split 的抽象实现了 left-split, right-split, corner-split,并且基于这些 split 实现了各式各样的画作。
这个例子生动形象的展示了数据抽象 painter 千姿百态各式各样的实现,以及这种数据屏障带来的隔离是如何强大,自然,transform-painter 这样根植于数据抽象的,对业务进行很好提炼的高阶过程是让我们轻松使用数据抽象的关键。最后,这个例子展示了因为数据抽象和过程抽象产生的应用分层(分层意味着层内过程的代码依赖关系的范围较为集中,仅和上下层有交叉),以及这种分层对于系统带来的积极影响:我们可以在 split 高阶图形级别(这里有高阶过程抽象 square-split)、flip 等操作变换级别(这里有高阶过程抽象 transform-painter)、frame, segment 等具体实现级别(segments->painter)进行代码的修改。这种分层让我们可以将可变性进行很好的隔离,使得程序在不断开发和完善的过程中始终保持系统稳定与健壮。
总的来说,编程是一种艺术,我们总是需要易于理解的数据屏障(解放心智而非完全暴露)和深刻的过程抽象(增加抽象而非简单堆砌)以打造恰巧好的分层,将不变性和可变性隔离,增强系统稳定性的同时又不增加冗余,使得代码最易于理解。
符号数据
在之前的例子中,数据总是由数值出发构造起来的。为提升语言表述能力,需要引入任意符号作为数据的能力,其实现通常通过为数据对象添加引号来进行。加了引号的表达式被当做数据而非求值的表达式(即大声说出你的名字 vs 大声说出'你的名字'),因为 Scheme 有空白和括号隔离,因此引号只用一边即可,且必须是单引号,双引号表示一个字符串。引号这种方式违背了语言关于复合表达式都是用括号限定的规则,不具有表的形式,因此,可将引号看做 'a 看做 (quote a) 的语法糖。比如 (list 'a 'b 'c) 就是 (a b c),(list (list 'george)) 就是 ((george)),(cadr '((x1 x2) (y1 y2))) 就是 (y1 y2)。
为了对符号进行操作,引入一些基本过程:eq? 表示对两个符号是否相同的判断,基于此可实现 memq,其用来对一个 list 中是否包含特定符号进行判断。equals? 用来对两个 list 检查符号是否相同,其定义如下。
(define (memq item x)
(cond ((null? x) #f)
((eq? item (car x)) x)
(else (memq item (cdr x)))))
(define (equal? x y)
(cond ((and (symbol? x) (symbol? y)) (eq? x y))
((and (number? x) (number? y)) (= x y))
((and (list? x) (list? y))
(cond ((and (null? x) (null? y)) #t)
((or (null? x) (null? y)) #f)
((equal? (car x) (car y)) (equal? (cdr x) (cdr y)))
(else #f)))
(else #f)))
(printf "~s\n~s\n" (equal? '(this is a list) '(this is a list))
(equal? '(this is a list) '(this (is a) list)))
实例:符号求导
不区分数据和过程表示形式的特性赋予了 Lisp 操作符号时极大的便利,代码可以表示的很自然,而不是生硬的将数据和操作数据的过程隔离开来。在这个例子中,deriv 通过对如下五个规则的递归实现对函数表达式的求导,这里的函数表达式不再作为之前的高阶函数,而是通过符号数据来表示:

Scheme 通过 symbol? 过程来判断一个表达式是否是一个符号,配合 eq? 可以实现符号等同行检测。
(define (variable? e) (symbol? e)) ;e是变量吗
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2))) ;v1 和 v2 是同一变量吗
(define (=number? exp num) (and (number? exp) (= exp num)))
(define (single-operand? x) (null? (cdr x)))
接下来,我们需要构建求导所需的加法数据抽象,其包括一个谓词 sum? 用来检查语句的语法,一个 addend 和 augend 过程用来充当选择桉树,一个 make-sum 来构造加法数据对象,这里基础版本仅支持两个数相加 make-sum-simple,而高级版本则支持多个数相加 make-sum,对于后者而言,其实现原则就是如果是两个数则调用 make-sum-simple,如果是多个数,余下的数先不计算,仅表示,而在 augend 中通过积极的调用 make-sum 来进行计算。
(define (sum? e) (and (pair? e) (eq? (car e) '+))) ;e是和式吗
(define (addend e) (cadr e)) ;e的被加数
;加法运算基本定义(仅支持两个数)
(define (augend-simple e) (caddr e)) ;e的加数
(define (make-sum-simple a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list '+ a1 a2)))) ;构造a1 和 a2 的和式
;加法运算高级定义(支持多个加数)
(define (augend e)
(let ((tail (cddr e)))
(if (single-operand? tail)
(car tail)
(apply make-sum tail)))) ;e的加数
(define (make-sum a1 . a2)
(if (single-operand? a2)
(make-sum-simple a1 (car a2))
(cons '+ (cons a1 a2))))
乘法的谓词、选择函数和构造函数类似:
(define (product? e) (and (pair? e) (eq? (car e) '*))) ;e是乘式吗
(define (multiplier e) (cadr e)) ;e的被乘数
;乘法运算基本定义(仅支持两个数)
(define (multiplicand-simple e) (caddr e)) ;e的乘数
(define (make-product-simple m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2)))) ;构造 m1 和 m2 的乘式
;乘法运算高级定义(支持多个乘数)
(define (multiplicand e)
(let ((tail (cddr e)))
(if (single-operand? tail)
(car tail)
(apply make-product tail))))
(define (make-product m1 . m2)
(if (single-operand? m2)
(make-product-simple m1 (car m2))
(cons '* (cons m1 m2))))
阶乘也是如此:
;阶乘运算定义
(define (exponentiation? e) (and (pair? e) (eq? (car e) '**)))
(define (base e) (cadr e))
(define (exponent e) (caddr e))
(define (make-exponentiation e1 e2)
(cond ((=number? e2 0) 1)
((=number? e2 1) e1)
(else (list '** e1 e2))))
最后这里实现了求导过程,基本上就是判断条件,化简递归:
;求导过程实现
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
((exponentiation? exp)
(make-product
(make-product ((exponent exp)
(make-exponentiation (base exp)
(- (exponent exp) 1))))
(deriv (base exp) var)))
(else (error "unknow expression type -- DERIV" exp))))
(printf "~s\n" (deriv '(+ x 3) 'x))
(printf "~s\n" (deriv '(* x y) 'x))
(printf "~s\n" (deriv '(* (* x y) (+ x 3)) 'x))
(printf "~s\n" (deriv '(* x y (+ x 3)) 'x)))
如果对于 Lisp 使用前缀表示理解不透彻,下面使用中缀表示的版本则充分展现了计算的复杂性,这种复杂性来自于前缀表达式可自然传递多个参数,且每个运算都使用括号区分,因此非常方便解构,而中缀表达式则包含自然的运算符优先级,这种括号是隐含的:3 + 4 * 2,因此无法通过仅修改谓词、选择函数和构造函数来达到目的。因此下面的实现仅支持“热爱括号”的两元中缀运算,如果需要实际使用,可以对传入的表达式先通过栈根据优先级修复为这种带有括号的形式(LeetCode 很常见的算法),然后再进行计算。注意这里相比较前缀运算基本仅修改了选择函数,让其按照数据格式来进行选择,此外对于构造函数,按照中缀表示进行构造,而 deriv 得益于数据抽象(加法、乘法)而完全不用更改。这里体现了数据抽象良好的分层带来的封装性对系统可靠的有益影响。
;基本过程定义
(define (variable? e) (symbol? e)) ;e是变量吗
(define (same-variable? v1 v2)
(and (variable? v1) (variable? v2) (eq? v1 v2))) ;v1 和 v2 是同一变量吗
(define (=number? exp num) (and (number? exp) (= exp num)))
(define (single-operand? x) (null? (cdr x))) ;x + (3 + 4)
;加法运算基本定义
(define (sum? e) (and (pair? e) (eq? (cadr e) '+) (not (null? (cddr e))))) ;e是和式吗
(define (addend e) (car e)) ;e的被加数
;加法运算基本定义(仅支持两个数)
(define (augend e) (caddr e)) ;e的加数
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list a1 '+ a2)))) ;构造a1 和 a2 的和式
; ;加法运算高级定义(支持多个加数)
; (define (augend e) ;(a + b + c + d)
; (let ((tail (cddr e)))
; (if (single-operand? tail)
; (car tail) ;(b) -> b or (b + c + d) -> ? 错误,这里有乘法优先级问题
;这里充分体现了前缀表达式在传递多个参数上的优势,根本无需担心运算符改变问题
; (cond ((sum? tail) (apply make-sum tail))
; ((product? tail) (apply make-product tail)))))) ;e的加数
;乘法运算基本定义
(define (product? e) (and (pair? e) (eq? (cadr e) '*) (not (null? (cddr e))))) ;e是乘式吗
(define (multiplier e) (car e)) ;e的被乘数
;乘法运算基本定义(仅支持两个数)
(define (multiplicand e) (caddr e)) ;e的乘数
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list m1 '* m2)))) ;构造 m1 和 m2 的乘式
;求导过程实现
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else (error "unknow expression type -- DERIV" exp)))
(printf "~s\n" (deriv '(x + 3) 'x))
(printf "~s\n" (deriv '(x * y) 'x))
(printf "~s\n" (deriv '((x * y) * (x + 3)) 'x)))
实例:集合的表示
下面是一个例子,介绍了如何表示高效表示集合(不重复列表)数据抽象。其 API 定义(构造和选择函数)如下所示,可判断元素是否属于集合,将元素添加到集合,求集合的交集和并集。
; (define (element-of-set? e u) ???)
; (define (adjoin-set s u) ???)
; (define (union-set u1 u2) ???)
; (define (intersection-set u1 u2) ???)
最简单的实现方法是使用一个未经排序的列表表示,每次判断都需要 θ(n) 以遍历确认是否存在,每次添加都需要 θ(n) 以遍历并插入(如果没有的话)。对于并集的计算,需要对集合 A 的每个元素在集合 B 中进行存在判断,时间复杂度 θ(n^2)。对于交集的计算也是如此。
;不允许重复的未排序数据抽象
(define (element-of-set? e u)
(cond ((null? u) #f)
((equal? e (car u)) #t)
(else (element-of-set? e (cdr u)))))
(define (adjoin-set s u)
(if (element-of-set? u s) u (cons s u)))
(define (union-set u1 u2)
(fold (lambda (ele-of-u2 u1-now)
(if (element-of-set? ele-of-u2 u1-now)
u1-now
(cons ele-of-u2 u1-now))) u1 u2))
(define (intersection-set u1 u2)
(cond ((or (null? u1) (null? u2)) '())
((element-of-set? (car u1) u2)
(cons (car u1) (intersection-set (cdr u1) u2)))
(else (intersection-set (cdr u1) u2))))
(printf "~s ~s ~s\n" (element-of-set? 1 '(1 2 3))
(element-of-set? 1 '(2 3))
(element-of-set? 1 '()))
(printf "~s ~s\n" (union-set '(1 2 3) '(2 3 4))
(intersection-set '(1 2 3) '(2 3 4))))
为提高效率,使用允许重复的未排序序列来实现集合,现在查询存在的效率依旧是 θ(n),但插入数据的效率为 θ(1),交集和并集的效率没有提升,依旧是 θ(n^2)。
;允许重复的未排序数据抽象
(define (element-of-set? e u)
(cond ((null? u) #f)
((equal? e (car u)) #t)
(else (element-of-set? e (cdr u)))))
(define (adjoin-set s u) (cons s u))
(define (union-set u1 u2)
(fold (lambda (ele-of-u2 u1-now)
(if (element-of-set? ele-of-u2 u1-now)
u1-now
(cons ele-of-u2 u1-now))) u1 u2))
(define (intersection-set u1 u2)
(fold (lambda (ele-of-u2 res-now)
(if (and (element-of-set? ele-of-u2 u1)
(not (element-of-set? ele-of-u2 res-now)))
(cons ele-of-u2 res-now) res-now)) '() u2))
(printf "~s ~s ~s\n" (element-of-set? 1 '(1 2 2 3))
(element-of-set? 1 '(2 3))
(element-of-set? 1 '()))
(printf "~s ~s\n" (union-set '(1 2 2 3) '(2 3 3 4))
(intersection-set '(1 2 3 3) '(2 3 4 4)))
现在通过排序列表来重新定义集合实现,在这种情况下,判断元素存在有 θ(n) 的速度,插入元素有 θ(n) 的速度,而交集和并集的计算则因为排序而需要 θ(n) 的速度即可,相比较未排序实现提升明显。
;排序数据抽象
(define (element-of-set? e u)
(cond ((null? u) #f)
((= e (car u)) #t)
((< e (car u)) #f)
(else (element-of-set? e (cdr u)))))
(define (adjoin-set s u)
(if (null? u) (cons s '())
(let ((next (car u)))
(if (< s next) (cons s u)
(cons next (adjoin-set s (cdr u)))))))
(define (union-set u1 u2)
(cond ((null? u1) u2)
((null? u2) u1)
(else (let ((e1 (car u1)) (e2 (car u2)))
(cond ((= e1 e2) (cons e1 (union-set (cdr u1) (cdr u2))))
((> e1 e2) (cons e2 (union-set u1 (cdr u2))))
((< e1 e2) (cons e1 (union-set (cdr u1) u2))))))))
(define (intersection-set u1 u2)
(if (or (null? u1) (null? u2)) '()
(let ((e1 (car u1)) (e2 (car u2)))
(cond ((= e1 e2) (cons e1 (intersection-set (cdr u1) (cdr u2))))
((> e1 e2) (intersection-set u1 (cdr u2)))
((< e1 e2) (intersection-set (cdr u1) u2))))))
最后,我们使用二叉树来进一步改进基于排序的实现,二叉树相比较排序进一步提升了插入和判断等基础操作的效率,现在仅需要 θ(logn) 的步数即可完成判断和插入。为了实现二叉树,首先提供其抽象实现:entry 负责从数选取根节点,left-branch 和 right-branch 选取子树,make-tree 用来构造一棵树。
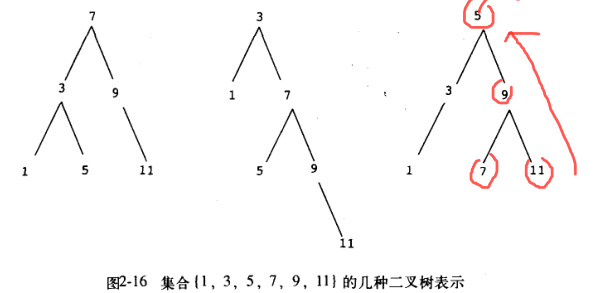
;基于二叉树实现的数据抽象
(define (entry tree) (car tree))
(define (left-branch tree) (cadr tree))
(define (right-branch tree) (caddr tree))
(define (make-tree entry left right) (list entry left right))
基于此二叉树的数据抽象,判断元素存在就可以看做对于根节点的比较,小则递归遍历左树,大则递归遍历右树,等则直接返回。插入元素也是如此,如果小则递归对左树插入,大则递归对右树插入,反之则返回此树,在根部构造无左右节点的子树挂在现有的树上。但是这样的二叉树依赖于随机的数据插入,如果数据有偏斜,那么二叉树不平衡,效率会急剧降低。
(define (element-of-set? x set)
(cond ((null? set) #f)
((= x (entry set)) #t)
((< x (entry set))
(element-of-set? x (left-branch set)))
((> x (entry set))
(element-of-set? x (right-branch set)))))
(define (adjoin-set x set)
(cond ((null? set) (make-tree x '() '()))
((= x (entry set)) set)
((< x (entry set))
(make-tree (entry set)
(adjoin-set x (left-branch set))
(right-branch set)))
((> x (entry set))
(make-tree (entry set)
(left-branch set)
(adjoin-set x (right-branch set))))))
最后,实现树和列表的转换函数,以方便构造树和后续平衡树的实现。这里提供了 append 和 copy-to-list 两种实现,前者基于递归,效率很低:对于每一层栈,append 都需要遍历前者所有元素以返回结果,后者基于迭代,效率较高。注意这里的核心思想是:分别对左树、当前值和右树进行处理,得到的结果就是有序的列表。
(define (tree->list-1 tree)
(if (null? tree) '()
(append (tree->list-1 (left-branch tree))
(cons (entry tree)
(tree->list-1 (right-branch tree))))))
(define (tree->list-2 tree) ;先解决左边值,然后解决其右边的兄弟值
;这种方式会下到最小的最左边节点,依次解决底层,弹出栈,往上游走
;直到根节点,然后在右侧子树也是如此,最后被解决的是最大的最右节点,
;其没有任何的左节点,向上依次弹出栈到根
(define (copy-to-list tree result-list)
(if (null? tree) result-list
(copy-to-list (left-branch tree)
(cons (entry tree)
(copy-to-list (right-branch tree)
result-list)))))
(copy-to-list tree '()))
(define t1 (make-tree 7
(make-tree 3 (make-tree 1 '() '()) (make-tree 5 '() '()))
(make-tree 9 '() (make-tree 11 '() '()))))
(define t2 (make-tree 3
(make-tree 1 '() '())
(make-tree 7
(make-tree 5 '() '())
(make-tree 9 '() (make-tree 11 '() '())))))
(define t3 (make-tree 5
(make-tree 3 (make-tree 1 '() '()) '())
(make-tree 9 (make-tree 7 '() '()) (make-tree 11 '() '()))))
最后我们定义从有序列表向树转换的方法,这里的实现也不复杂,只需要对列表分别处理左边一半、当前元素和右边一半,然后递归进行此过程即可。注意这里的递归很巧妙的利用了 elts 这个序列,其被指定处理 n 个元素,然后返回值告知我们尚未处理的元素。因此,在 list->tree 的最开始,传入了 elements 的length。
(define (list->tree elements)
(car (partial-tree elements (length elements))))
(define (partial-tree elts n)
(if (= n 0) (cons '() elts) ;如果没有需要处理的元素,则返回空树
(let ((left-size (quotient (- n 1) 2)))
(let ((left-result (partial-tree elts left-size))) ;先处理一半
(let ((left-tree (car left-result)) ;左边的树
(non-left-elts (cdr left-result)) ;左边尚未处理的元素
(right-size (- n (+ left-size 1)))) ;剩下的右边处理(除了当前根)
(let ((this-entry (car non-left-elts)) ;当前根
(right-result (partial-tree (cdr non-left-elts) right-size))) ;后处理一半
(let ((right-tree (car right-result)) ;右边的树
(remaining-elts (cdr right-result))) ;剩余未处理元素
(cons (make-tree this-entry left-tree right-tree)
remaining-elts)))))))) ;将左树和右树构造起来,剩余元素返回
下面提供了基于平衡二叉树实现的集合的 union-set 和 intersection-set,这里利用了对排序 union-set 和 intersection-set 的复用,先将树转换为有序列表,然后整合后,再构建平衡树。这种方式提供了 θ(n) 的效率,相比较排序序列实现一致,但基础操作:插入和查看的效率得以提升。
(define (union-set t1 t2)
(define (union-sorted-set u1 u2)
(cond ((null? u1) u2)
((null? u2) u1)
(else (let ((e1 (car u1)) (e2 (car u2)))
(cond ((= e1 e2) (cons e1 (union-sorted-set (cdr u1) (cdr u2))))
((> e1 e2) (cons e2 (union-sorted-set u1 (cdr u2))))
((< e1 e2) (cons e1 (union-sorted-set (cdr u1) u2))))))))
(list->tree (union-sorted-set (tree->list-2 t1) (tree->list-2 t2))))
(define (intersection-set t1 t2)
(define (intersection-sorted-set u1 u2)
(if (or (null? u1) (null? u2)) '()
(let ((e1 (car u1)) (e2 (car u2)))
(cond ((= e1 e2) (cons e1 (intersection-sorted-set (cdr u1) (cdr u2))))
((> e1 e2) (intersection-sorted-set u1 (cdr u2)))
((< e1 e2) (intersection-sorted-set (cdr u1) u2))))))
(list->tree (intersection-sorted-set (tree->list-2 t1) (tree->list-2 t2))))
最后,我们介绍了集合的一个实际用例:对数据库数据的查找,这里介绍了使用无排序集合和二叉树的方式,key 过程用于查找特定 entry 的数字索引,以在无排序集合或二叉树中进行导航。
(define (lookup given-key set-of-records)
(define (key set) ???)
(cond ((null? set-of-records) #f)
((equal? given-key (key (car set-of-records)))
(car set-of-records))
(else (lookup given-key (cdr set-of-records)))))
(define (lookup-2 given-key tree)
(define (key tree) ???)
(if (null? tree) #f
(let ((node (entry tree)))
(let ((node-key (key node)))
(cond ((= node-key given-key) node)
((< node-key given-key)
(lookup-2 given-key (right-branch tree)))
((> node-key given-key)
(lookup-2 given-key (left-branch tree))))))))
(printf " ~s\n ~s\n ~s\n" (tree->list-1 t1) (tree->list-1 t2) (tree->list-1 t3))
(printf " ~s\n ~s\n ~s\n" (tree->list-2 t1) (tree->list-2 t2) (tree->list-2 t3))
(printf "~s\n" (list->tree '(1 3 5 7 9 11)))
(printf "~s\n" (intersection-set (list->tree '(1 2 3 4 5)) (list->tree '(1 3 5 7 9))))
(printf "~s\n" (union-set (list->tree '(1 2 3 4 5)) (list->tree '(1 3 5 7 9)))))
实例:霍夫曼编码树
对于数据的存储而言,需要进行二进制的编码,如果需要区分 n 个字符,那么就需要 log2N 个二进制位,比如 A-H 的区分至少需要 3 位。这种方式简单并且直接,但是问题是浪费了存储资源,因为有一些字符出现的频次可能很高,其如果采用较短的编码方式将节省存储空间。基于此诞生了变长编码,莫尔斯码就是一种变长编码,为区分不同的数据,莫尔斯码需要在每个字符的点划后使用特殊分隔符。或者,也可以使用“前缀码”系统,即不同字符的前缀始终不同,通过一个前缀的二进制仅会得到一种对应的字母。变长编码如果能利用符号出现的频次地图来进行编码会显著节省存储空间,霍夫曼编码树就是根据符号频次构建其对应的二进制编码地图的一种技术。
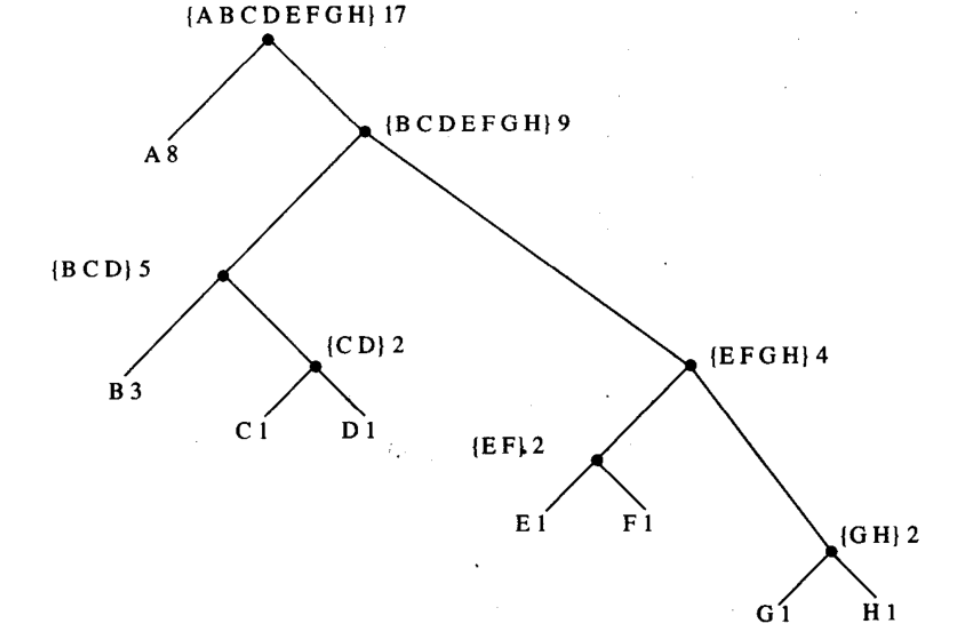
一颗包含 8 个字符的霍夫曼编码树如上图所示,其包含两种结构:leaf 总会包含一个字符与其出现的频次,tree 总能告诉我们它包含所有的字符和总频次。之所以使用二叉树形式是因为,二叉对应着 0 和 1,因此从一棵树的根开始查找,0 表示左分支,1 表示右分支,如果找到一个 leaf 就找到了此符号,反之继续根据二进制编码在 tree 中遍历,直到找到符号位置。二叉树相比较排序结构对搜索的友好决定了其效率最高。
根据上述结构定义 leaf 和 tree 的数据抽象,这里 leaf 使用一个列表实现,额外的 'leaf 用来表示这是一个 leaf 节点,选择函数 leaf? 根据此 'leaf 符号来判断是否是一个 leaf 节点,symbol-leaf 和 weight-leaf 用来从 leaf 节点选择其存储的符号和权重。make-code-tree 是 tree 的构造函数,包含了递归的左树和右树,并存储了所有符号的列表(方便查找),所有符号的权重,选择函数 left-branch 和 right-branch 用来选择左右树,symbols 和 weight 用来返回 tree/leaf 的符号集合和权重和。
(define (make-leaf symbol weight) ;制作字典节点
(list 'leaf symbol weight))
(define (leaf? obj)
(eq? (car obj) 'leaf))
(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))
(define (make-code-tree left right) ;制作字典
(list left right
(append (symbols left) (symbols right))
(+ (weight left) (weight right))))
(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
(if (leaf? tree) (list (symbol-leaf tree))
(caddr tree)))
(define (weight tree)
(if (leaf? tree) (weight-leaf tree)
(cadddr tree)))
decode 方法用来对一串 0 和 1 进行解码,方法很简单,根据数据在 tree 中导航,直到找到 leaf 取出符号为止,然后依次将多个符号取出来返回集合。
(define (decode bits tree) ;根据二进制导航左右 branch 解码
(define (choose-branch bit branch)
(cond ((= bit 0) (left-branch branch))
((= bit 1) (right-branch branch))
(else (error "bad bit from choose-branch" bit))))
(define (decode-1 bits current-branch)
(if (null? bits) '()
(let ((next-branch (choose-branch (car bits) current-branch)))
(if (leaf? next-branch)
(cons (symbol-leaf next-branch)
(decode-1 (cdr bits) tree))
(decode-1 (cdr bits) next-branch)))))
(decode-1 bits tree))
encode 方法用来将一串符号进行编码,对于每一个符号,都通过 tree 判断左树和右树是否包含,然后进入左树记下 0 右树记下 1,最后得到一个符号的 0 1 序列,不断如此,得到所有符号的 0 1 序列。
(define (encode message tree)
;对消息 message 通过 tree 字典进行编码,返回二进制序列
(define (contains items x)
(cond ((null? items) #f)
((eq? (car items) x) #t)
(else (contains (cdr items) x))))
(define (encode-symbol x tree)
(cond ((leaf? tree) '())
((contains (symbols (left-branch tree)) x)
(cons 0 (encode-symbol x (left-branch tree))))
((contains (symbols (right-branch tree)) x)
(cons 1 (encode-symbol x (right-branch tree))))
(else (error "not found symbol in tree" x))))
(define (encode-inner message)
(if (null? message) '()
(append (encode-symbol (car message) tree)
(encode-inner (cdr message)))))
(encode-inner message))
下面是一个简单的霍夫曼编码图以及其编码和解码的示意:
(define sample-tree
(make-code-tree
(make-leaf 'A 4)
(make-code-tree
(make-leaf 'B 2)
(make-code-tree
(make-leaf 'D 1)
(make-leaf 'C 1)))))
(define codec-message (encode '(B B D C A C) sample-tree))
(define decode-message (decode codec-message sample-tree))
(printf "~s ~s\n" codec-message decode-message)
为了方便构造编码 tree,提供如下方法,其接受符号和频次,通过 make-leaf-set 按照频次排序后构造为 leaf,然后将 leaf 转换为 tree。
(define (generate-huffman-tree pairs)
(define (adjoin-set x set) ;将 x 插入到有序 set 中
(cond ((null? set) (list x))
((> (weight x) (weight (car set))) (cons x set))
(else (cons (car set) (adjoin-set x (cdr set))))))
(define (make-leaf-set pairs)
;将 ((A 4) (B 2) (C 1)) 转换为排序 leaf 集合
(if (null? pairs) '()
(let ((pair (car pairs)))
(adjoin-set (make-leaf (car pair) (cadr pair))
(make-leaf-set (cdr pairs))))))
(define (successive-merge set)
(if (null? set) (make-leaf 'EOF -1)
(make-code-tree
(car set) (successive-merge (cdr set)))))
(successive-merge (make-leaf-set pairs)))
下面是一个自定义的 ABC 符号频次的 tree,最高频次在最上面,其路径最短,使用一个 0 即可编码。
(define h-tree (generate-huffman-tree '((A 4) (B 3) (C 2))))
(printf "~s\n~s\n~s\n" h-tree
(encode '(C A B) h-tree)
(decode '(1 1 0 0 1 0) h-tree))
; ((leaf A 4)
; ((leaf B 3)
; ((leaf C 2)
; (leaf END -1)
; (C END)
; 1)
; (B C END)
; 4)
; (A B C END)
; 8)
下面是一个实际的例子,对于这 8 个符号,如果定长编码,需要每个符号使用 log28 = 3 位,因此总共编码如下 36 个符号需要 36 * 3 = 108 位,而霍夫曼编码树则仅需要 88 位。
(define rock-tree (generate-huffman-tree
'((A 2) (BOOM 1) (NA 16) (SHA 3) (GET 2) (YIP 9) (JOB 2) (WAH 1))))
(define codec-rock
(encode '(GET A JOB
SHA NA NA NA NA NA NA NA NA
GET A JOB
SHA NA NA NA NA NA NA NA NA
WAH YIP YIP YIP YIP YIP YIP YIP YIP YIP
SHA BOOM) rock-tree))
(printf "~s\nlength:~d\n" codec-rock (length codec-rock))
抽象数据的多重表示
从理想的角度来说,基于某个数据抽象以及其构建的抽象屏障进行工作可以极大减轻认知负担,并且可提供实现可更改性这一松耦合的“构造系统方法学”的最佳实践。但软件系统往往是多人协作,且在时间维度不断成长起来的,要求跨时间和人员维护某一数据抽象并无可能。本小节提供的解决方案“抽象数据的多重表示”可解决这一问题。比如要对复数进行表示,介于不同计算的方便程度,可有两种数据表示方法:直角坐标和极坐标。其构造和选择函数如下所示:
;如果采用直角坐标表示
;x = rcosA, y = rsinA, r = √(x*x + y*y), a = arctan(y,x)
(define (make-from-real-imag x y) (cons x y))
(define (make-from-mag-ang r a)
(cons (* r (cos a)) (* r (sin a))))
(define (real-part x) (car x))
(define (imag-part x) (cadr x))
(define (magnitude x)
(sqrt (+ (square (real-part x))
(square (imag-part x)))))
(define (angle x)
(atan (imag-part x) (real-part x)))
;如果采用极坐标形式
(define (make-from-real-imag x y)
(cons (sqrt (+ (* x x) (* y y))) (atan y x)))
(define (make-from-mag-ang r a) (cons r a))
(define (real-part x) (* (magnitude x) (cos (angle x))))
(define (imag-part x) (* (magnitude x) (sin (angle x))))
(define (magnitude x) (car x))
(define (angle x) (cadr x))
基于复数构造和选择函数的计算过程如下所示,其不论在哪种表示方式下都能正常工作:
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2))))
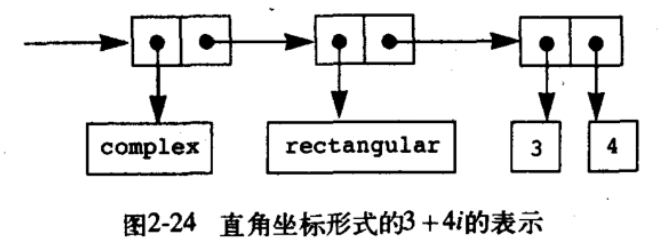
可以说,不管哪种表示,这都是又一个经典的数据抽象的例子。但问题在于,我们如何整合多种表示方式,毕竟不同表示方式的存在有客观和主观性:一套代码总是会存在对同一数据的不同侧面抽象,那么如何将其整合起来?需要注意,这里“抽象数据的多重表示”不同于“数据抽象的不同实现”,实现方式指的是使用 cons, list 或基本数字等低级数据结构和过程来实现复数这一高级数据抽象,而表示方式指的是复数这一数据抽象的不同展现方面。虽然它们都涉及到选择函数和构造函数过程,但实现方式位于数据抽象的低层,而表示方式则位于数据抽象同一层 —— 换言之,每种表示方式都可以使用多种实现方式进行实现,其层次结构如下所示:

为了将不同数据抽象的表示方式和使用复数的程序解耦,我们并不需要做太多的事情:只需要提供不同的构造函数和选择函数即可,应用程序将无差别调用这些过程。但实际上,如果想要将多种数据抽象表示整合起来,这里确实有工程上的问题:最基础的,对于一个对偶,如何知道它是基于极坐标还是直角坐标表示的呢?一般而言,有三种方式来解决这一问题:带标志数据、数据导向、消息传递。
其中标志数据的含义是,构造函数返回的复数数据添加一个类型标记符号,选择函数根据类型符号来决定实现方式,这种方式最容易理解,但缺点是不具备可加性,当添加新数据和过程时,为了避免过程名称冲突,所有之前的构造函数和选择函数都要重新命名。下面三个过程实现了打标签和获取标签,内容:
(define (label-usage)
(define (attach-tag type content) (cons type content))
(define (type-tag datum)
(if (pair? datum) (car datum) (error "no tag find" datum)))
(define (contents datum)
(if (pair? datum) (cdr datum) (error "no content find" datum)))
如下两个过程实现了带标签数据的标签判定:
(define (rectangular? z) (eq? (type-tag z) 'rectangular))
(define (polar? z) (eq? (type-tag z) 'polar))
下面是基于直角坐标的实现 -r 以及基于极坐标的实现 -p:
(define (make-from-real-imag-r x y)
(attach-tag 'rectangular (cons x y)))
(define (make-from-mag-ang-r r a)
(attach-tag 'rectangular
(cons (* r (cos a)) (* r (sin a)))))
(define (real-part-r x) (car x))
(define (imag-part-r x) (cadr x))
(define (magnitude-r x)
(sqrt (+ (square (real-part-r x))
(square (imag-part-r x)))))
(define (angle-r x)
(atan (imag-part-r x) (real-part-r x)))
(define (make-from-real-imag-p x y)
(attach-tag 'polar
(cons (sqrt (+ (* x x) (* y y))) (atan y x))))
(define (make-from-mag-ang-p r a)
(attach-tag 'polar (cons r a)))
(define (real-part-p x) (* (magnitude-p x) (cos (angle-p x))))
(define (imag-part-p x) (* (magnitude-p x) (sin (angle-p x))))
(define (magnitude-p x) (car x))
(define (angle-p x) (cadr x))
为了让其向应用程序提供统一的数据屏障视图,这里要根据标签数据类型进行构造函数和选择函数的分派:
(define (real-part z)
(cond ((rectangular? z)
(real-part-r (contents z)))
((polar? z)
(real-part-p (contents z)))))
(define (imag-poart z)
(cond ((rectangular? z)
(imag-part-r (contents z)))
((polar? z)
(imag-part-p (contains z)))))
(define (magnitude z)
(cond ((rectangular? z)
(magnitude-r (contents z)))
((polar? z)
(magnitude-p (contents z)))))
(define (angle z)
(cond ((rectangular? z)
(angle-rectangular (contents z)))
((polar? z)
(angle-polar (contents z)))))
(define (make-from-real-imag x y) (make-from-real-imag-r x y))
(define (make-from-mag-ang r a) (make-from-mag-ang-p r a))
数据导向的程序设计风格相比较带标签数据,具备了可加性:即新增加的复数数据抽象表示可以轻松和之前的表示互相融合,无需修改之前代码。所谓的数据导向,其实就是使用一个 map 把过程放在一起,其中不同的过程名和类型作为 key,不同的表示方式往 map 中写数据,而接口构造函数和选择函数通过从这个 map 中根据数据标签类型调用对应名称过程。这里的 get 和 put 就实现了这一功能:
(define operation-table (make-table))
(define get (operation-table 'lookup-proc))
(define put (operation-table 'insert-proc!))
不同的表示方式被作为不同的 package,其中将每个选择函数和构造函数加入到了 map 中。
(define (install-r-package)
(define (make-from-real-imag x y) (cons x y))
(define (make-from-mag-ang r a)
(cons (* r (cos a)) (* r (sin a))))
(define (real-part x) (car x))
(define (imag-part x) (cadr x))
(define (magnitude x)
(sqrt (+ (square (real-part x)) (square (imag-part x)))))
(define (angle x) (atan (imag-part x) (real-part x)))
(define (tag x) (attach-tag 'rectangular x))
(put 'real-part '(rectangular) real-part)
(put 'imag-part '(rectangular) imag-part)
(put 'magnitude '(rectangular) magnitude)
(put 'angle '(rectangular) angle)
(put 'make-from-real-imag 'rectangular
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'rectangular
(lambda (r a) (tag (make-from-mag-ang r a)))))
(define (install-p-package)
(define (make-from-real-imag x y)
(cons (sqrt (+ (* x x) (* y y))) (atan y x)))
(define (make-from-mag-ang r a) (cons r a))
(define (real-part x) (* (magnitude x) (cos (angle x))))
(define (imag-part x) (* (magnitude x) (sin (angle x))))
(define (magnitude x) (car x))
(define (angle x) (cadr x))
(define (tag x) (attach-tag 'polar x))
(put 'real-part '(polar) real-part)
(put 'imag-part '(polar) imag-part)
(put 'magnitude '(polar) magnitude)
(put 'angle '(polar) angle)
(put 'make-from-real-imag 'polar
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'polar
(lambda (r a) (tag (make-from-mag-ang r a)))))
最后通过 apply-generic 过程来帮助接口过程进行调用,这里基本就是剥离标签并调用对应过程:
(define (type-tag datum)
(if (pair? datum) (car datum) (error "no tag find" datum)))
(define (apply-generic op . args)
(let ((type-tags (map type-tag args)))
(let ((proc (get op type-tags)))
(if proc
(apply proc (map contents args))
(error "no method found." (list op type-tags))))))
(define (real-part z) (apply-generic 'real-part z))
(define (imag-part z) (apply-generic 'imag-part z))
(define (magnitude z) (apply-generic 'magnitude z))
(define (angle z) (apply-generic 'angle z))
(define (make-from-real-imag x y)
((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
((get 'make-from-mag-ang 'polar) r a))
数据导向的程序设计赋予了数据抽象多重表示以可加性,这极大增强了实践中数据抽象的灵活性和可用性。下面是一个对于之前提到的求导函数利用数据导向设计的修改:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else (error "unknow expression type -- DERIV" exp))))
(define (deriv-2 exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
(else ((get 'deriv (operator exp)) (operands exp) var))))
(define (operator exp) (car exp))
(define (operands exp) (cdr exp))
(put 'deriv '+ (lambda (operands var)
(let ((exp (cons '+ operands)))
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))))
(put 'deriv '* (lambda (operands var)
(let ((exp (cons '* operand)))
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))))
除了数据导向设计,还有一种选择称之为消息传递风格,用 2000 年时髦的话说就是面向对象设计思想,虽然 OOP 后来分裂成了 Java 式传统 Method Call 和 Actor 两种范式,但其含义还是一致的,即将不同数据抽象的同一表示聚集起来,放在一个实体中(一般是构造函数),调用不同实体的方法即可通过不同数据抽象表示进行工作。这种方式自然而然的实现了模块化,代码看上去也更加清爽,这里的概念基本上也对应了 OOP 的概念:构造函数,类,类实例和方法调用。因为消息传递和不同客体间的交流沟通非常类似,因此消息传递风格多用于模拟仿真。
(define (make-from-real-imag x y)
(define (dispatch op)
(cond ((eq? op 'real-part) x)
((eq? op 'imag-part) y)
((eq? op 'magnitude)
(sqrt (+ (square x) (square y))))
((eq? op 'angle) (atan y x))
(else (error "unknown op" op))))
dispatch)
(define (make-from-mag-ang r a)
(lambda (op)
(cond ((eq? op 'real-part) (* r (cos a)))
((eq? op 'imag-part) (* r (sin a)))
((eq? op 'magnitude) r)
((eq? op 'angle) a))))
(define (apply-generic op arg) (arg op))
当然,消息传递也有弊端,其一就是这里模块和构造函数合一的设计导致数据抽象实际上被分裂在这个模块闭包中(所谓类实例),我们传入的是底层的 x y r a,调用的也是基本过程,数据抽象变得不再可见。当然,就简单使用来说,这种方式构造数据抽象,使用数据抽象一气呵成,代码看上去更简单了,但实际上也丢失了外部扩展性(不修改代码的情况下),我们无法再基于复数这个数据抽象构建生态过程,打造数据屏障了 —— 除非修改这个一体的构造函数。
就本质而言,消息传递和数据导向设计风格的区别在于其操作数据抽象的着眼点不同:消息传递着眼于类型,将不同操作归到同一类型实例(闭包)下,数据导向着眼于操作,将不同类型的相同操作通过标签进行区分。
就扩展而言,消息传递在“增加过程”的可扩展性上表现很差,只允许在唯一的位置增加过程,且修改后每个实例化的类实例(闭包)都要重新加载,但是在“增加类型”上的可扩展性表现较好(尤其是静态语言中),无需修改至其他数据抽象表现形式的代码。而数据导向则在“增加过程”的可扩展性上表现很好,但有时候可能会显得零散,在“增加类型”的可扩展性上表现较好(尤其是动态语言中)。
在大部分情况下,如果不是业务有天然的 > 3 个类型(比如仿真模拟、GUI),数据导向的这种处理方式灵活性更高:数据抽象被暴露而非隐藏可以更方便的扩展并基于此数据抽象打造抽象屏障。
数据抽象的层次(带有通用型操作的系统)
上一节介绍的“数据的多重表示”中,我们发现了一种极具扩展性的“数据导向”设计风格,基于这种风格,我们可以在多个类似的数据抽象上继续进行抽象(将有理数、复数和常规算数的数据抽象继续延伸为数的抽象),就像在第一章对过程抽象继续进行抽象一样(一般函数 -> 传入函数的高阶函数 -> 生成函数的高阶函数)。
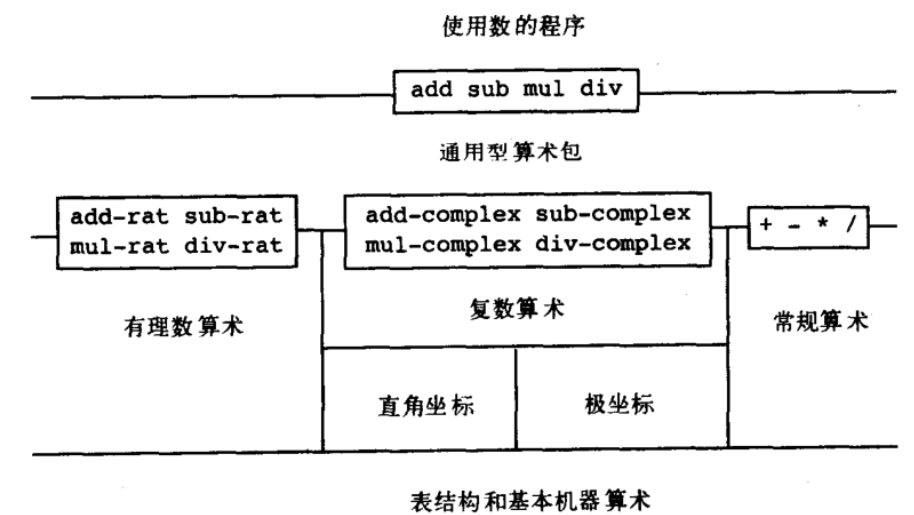
下面是通用的基于数的数据抽象的加减乘除过程,其通过查找 x 和 y 的类型,并在 map 中调用此类型的对应方法并执行。install-basic-number 是基础的运算,install-rational 是无理数运算,install-complex 是复数运算,在这里我们向 map 中安装了对应类型的过程。注意“数据导向”设计风格是基于过程进行的切面,因此如果需要实现一个过程,则需要为不同类型均实现此过程,比如 equ?,“消息传递”设计风格是基于类型进行的切面,其实现过程也需要为每个类型进行实现,区别在于,前者在任何地方都可以扩展,只要放到 map 中即可,而后者则必须修改构造函数 —— 如果无法修改的话,要使用派生子类的技术。
(define (add x y) (apply-generic 'add x y))
(define (sub x y) (apply-generic 'sub x y))
(define (mul x y) (apply-generic 'mul x y))
(define (div x y) (apply-generic 'div x y))
(define (equ? x y) (append-generic 'equ x y))
(define (install-basic-number)
(define (tag x) (attach-tag 'scheme-number x))
(put 'add '(scheme-number scheme-number)
(lambda (x y) (tag (+ x y))))
(put 'sub '(scheme-number scheme-number)
(lambda (x y) (tag (- x y))))
(put 'mul '(scheme-number scheme-number)
(lambda (x y) (tag (* x y))))
(put 'div '(scheme-number scheme-number)
(lambda (x y) (tag (/ x y))))
(put 'make 'scheme-number
(lambda (x) (tag x)))
(put 'equ? 'scheme-number
(lambda (x y) (= x y)))
'done)
(define (make-scheme-number n)
((get 'make 'scheme-number) n))
(define (install-rational)
(define (number x) (car x))
(define (denom x) (cdr x))
(define (make-rat n d) (let ((g (gcd n d)))
(cons (/ n g) (/d g))))
(define (add-rat x y)
(make-rat (+ (* (number x) (denom x))
(* (number y) (denom y)))
(* (denom x) (denom y))))
(define (sub-rat x y)
(make-rat (- (* (number x) (denom y))
(* (number y) (denom x)))
(* (denom x) (denom y))))
(define (mul-rat x y)
(make-rat (* (number x) (number y))
(* (denom x) (denom y))))
(define (div-rat x y)
(make-rat (* (number x) (denom y))
(* (denom x) (number y))))
(define (tag x) (attach-tag 'rational x))
(put 'add '(rational rational)
(lambda (x y) (tag (add-rat x y))))
(put 'sub '(rational rational)
(lambda (x y) (tag (sub-rat x y))))
(put 'mul '(rational rational)
(lambda (x y) (tag (mul-rat x y))))
(put 'div '(rational rational)
(lambda (x y) (tag (div-rat x y))))
(put 'equ? '(rational rational)
(lambda (x y)
(let ((zero (sub-rat x y)))
(and (= (number zero) 0) (= (denom zero) 0)))))
'done)
(define (make-rational n d)
((get 'make 'rational) n d))
复数的实现值得一提。这里我们为 complex 的分派没有直接实现,其会通过 make-from-xxx 继续在 map 中通过 rectangular 或 polar 继续分派以解决加减和乘除问题(类似继承链的分派)。
(define (install-complex-pakcage)
(define (make-from-real-imag x y)
((get 'make-from-real-imag 'rectangular) x y))
(define (make-from-mag-ang r a)
((get 'make-from-mag-ang 'polar) r a))
(define (add-complex z1 z2)
(make-from-real-imag (+ (real-part z1) (real-part z2))
(+ (imag-part z1) (imag-part z2))))
(define (sub-complex z1 z2)
(make-from-real-imag (- (real-part z1) (real-part z2))
(- (imag-part z1) (imag-part z2))))
(define (mul-complex z1 z2)
(make-from-mag-ang (* (magnitude z1) (magnitude z2))
(+ (angle z1) (angle z2))))
(define (div-complex z1 z2)
(make-from-mag-ang (/ (magnitude z1) (magnitude z2))
(- (angle z1) (angle z2))))
(define (tag x) (attach-tag 'complex x))
(put 'add '(complex complex)
(lambda (z1 z2) (tag (add-complex z1 z2))))
(put 'sub '(complex complex)
(lambda (z1 z2) (tag (sub-complex z1 z2))))
(put 'mul '(complex complex)
(lambda (z1 z2) (tag (mul-complex z1 z2))))
(put 'div '(complex complex)
(lambda (z1 z2) (tag (div-complex z1 z2))))
(put 'make-from-real-imag 'complex
(lambda (x y) (tag (make-from-real-imag x y))))
(put 'make-from-mag-ang 'complex
(lambda (r a) (tag (make-from-mag-ang r a))))
(put 'equ? '(complex complex)
(lambda (x y)
(let ((zero (sub-complex x y)))
(and (= (real-part zero) 0)
(= (imag-part zero) 0)))))
'done)
(define (make-complex-from-real-imag x y)
((get 'make-from-real-imag 'complex) x y))
(define (make-complex-from-mag-ang r a)
((get 'make-from-mag-ang 'complex) r a))
这里还有一个恼人的问题,我们的数据抽象层次并不智能:如上所示,如果是 'complex 类型的数据要进行 magnitude 将会出错,Scheme 不知道 'complex 是一种 'polar 或 'rectangular。因此要为此 'complex 单独注册过程到 map:

此外,目前我们的实现只能处理两个同类型数据,如果要对一个复数和一个简单数据相加则无法处理。解决办法之一是为每种类型 pair 都注册对应过程到 map 中,这种方法非常笨拙。或者可以使用“强制”的技术(类似于 Java 的自动类型转换),强制依赖于类型层次,在这个例子中,类型层次很容易定义,如下图所示,而在另外一些类型系统中,类型层次就不是那么显而易见的了,最典型的问题就是菱形继承。
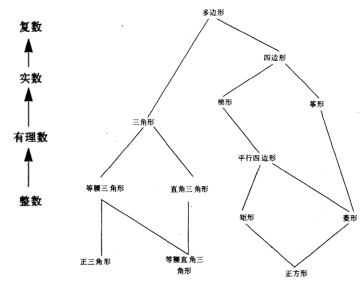
对于具体的实现而言,我们将“强制”放在另一张 map 中,通过 put-coercion 和 get-coercion 来注册允许的类型转换,比如 complex->scheme-number,然后重写 apple-generic 方法,这里为了简单只处理了两个参数的过程,如果其类型不匹配,则从“强制”表中查找将一种类型转换为另一种类型的过程,如果找到则转换后再应用。这种实现还是比较脆弱的,考虑定义一个 scheme-number->scheme-number 的强制过程,不同类型的转换会导致解释器卡死(因此需要在获取 t1->t2 和 t2->t1 时前进行一下 t1 和 t2 的检查,如果两个类型相同,且无法在基本 map 找到,则不使用强制)。

一个更为健壮的实现不仅要考虑 > 2 的参数,还需要考虑上升和下降的层次,以在类型层次间进行导航并找到可用的特殊 map 过程以进行转换。下面是几种 raise 的实现,其可搭配 apply-generic 进行逐步的类型转换尝试(就好像 Java 那样,Java 可对静态分派的方法进行参数的类型对比和转换以选择最合适的方法):
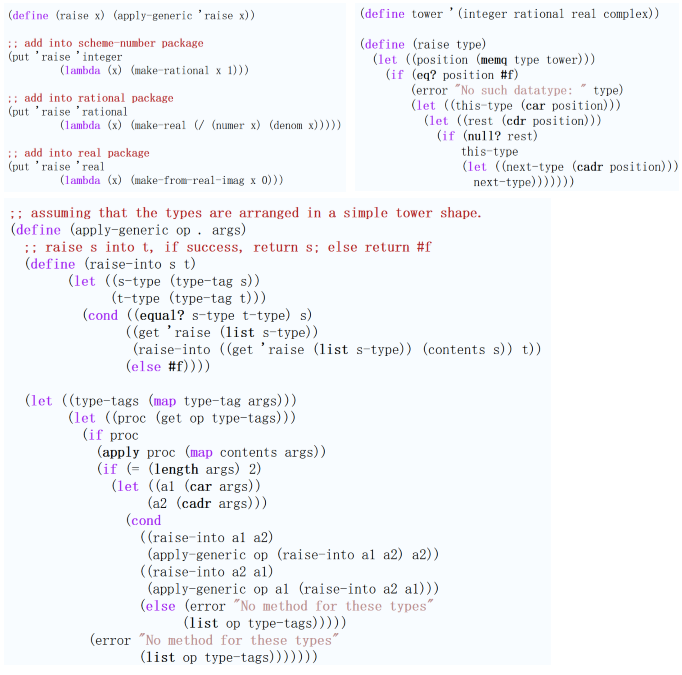
消息传递风格 (无状态面向对象) 中的数据和过程抽象
面向对象是一种软件开发的设计思想,其主要试图解决大型工程的复杂性问题,解决方案主要包含两个方面:①在静态结构上使用消息传递风格实现数据和过程抽象;②在动态发展中引入时间维度并且在封闭消息的模块中使用局部状态。第二点在下一章阐述,这里主要讲解面向对象的消息传递风格实现的抽象。
消息传递风格和“数据抽象多种表现形式和层次”的标签方法、数据导向风格不同:构造函数和选择函数现在被划归到被称之为“类”的模块中,变为类构造器和实例方法,暴露的抽象数据现在被隐藏(或者说合一成为类对象),此外数据抽象的屏障 —— 一般过程现在转身成为静态方法(在 Scala 或 Kotlin 中指的是伴生对象的方法),这种“紧凑”的表示自然而然的实现了代码的模块化。此外,数据抽象的多重表示、数据抽象的层次在消息传递的面向对象思想中被映射为类的继承关系以及接口系统,这套系统很容易使用,且易于理解。换言之,无状态的面向对象因数据抽象而起,糅合了过程抽象,实现了很好的模块化。这种糅合为数据抽象的构造提供了极大的方便,且在层次性过程抽象中也能很好的工作(类本质就是一个带有闭包过程,对象就是此过程的一个闭包实例,之前返回过程的高阶过程现在可以返回一般过程,也可以返回对象,它们本质都是过程,返回对象的缺点是在纯粹的过程抽象中掺杂了数据抽象(返回函数的高阶函数和一个返回 Java 对象的普通 Java 静态方法没有什么本质区别,Java 对象本质就是一个带有闭包的函数,不过带有数据抽象的性质),优点是提供了对于闭包更丰富的操作,有得有失)。
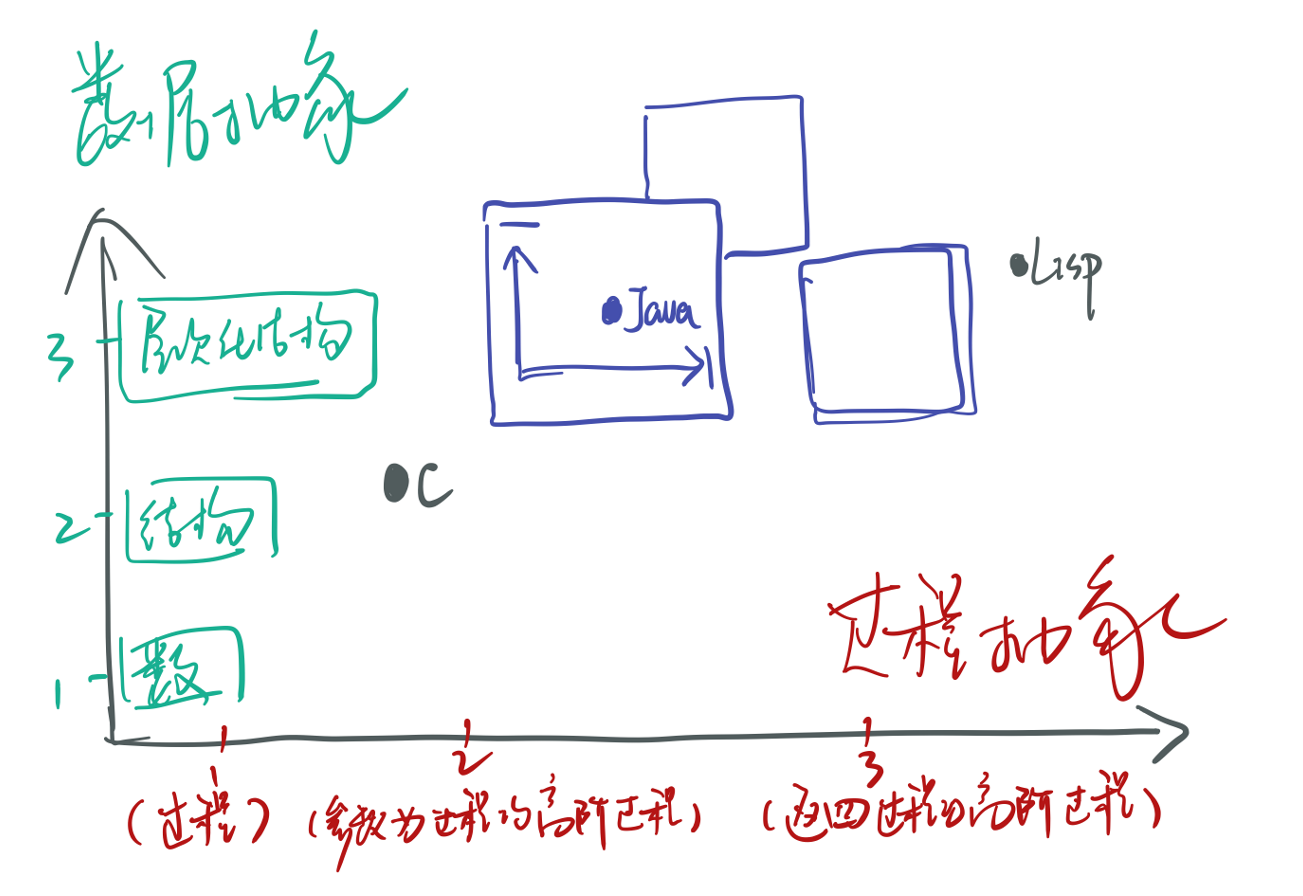
但是,也要看到这种糅合的不足,这种将“数据抽象”隐藏在类中的方式虽然提高了模块性,但不利于数据抽象的抽象屏障的扩展 —— 增加一个新的构造函数、增加新的过程。换言之,现在的扩展将不得不拘泥于模块:在面向对象的实践中,为了扩展一个数据抽象的过程,不得不使用继承或组合来创建一个新类,虽然现代面向对象理念更倾向于组合而非继承,但坦白来说,一个类代表了对数据的一层抽象,不论是组合还是继承,这些新增加的类并没有抽象任何数据,仅仅是为了扩展一个数据抽象过程,这导致了面向对象工程严重的冗余分层。一种解决方案是为面向对象引入函数式编程理念,将新的构造函数、过程放到工具类中,传入此类实例来进行调用实现数据抽象和过程抽象的扩展。
从近二十年(也是 Java 诞生以来的软件工程领域经验)来看,无状态的面向对象是一种简化了数据抽象、过程抽象,并天生支持模块化的开发模式,这种模式容易理解,支持大规模工程化,但传统的经典面向对象风格其实也极大了束缚了数据和过程的抽象水平,降低了代码的抽象能力。造成问题的根源在于这种糅合对于数据抽象的选择过程与一般过程的混淆,以及为基本过程开放了访问底层数据抽象实现的过多权限:大量开发者意识不到过程抽象应该使用静态方法而非类实例方法实现:①偷懒定义的选择过程(类实例方法)越来越多,过程抽象(静态方法)偏少 —— 类实例方法太简单好用了,看起来效率也高 —— 这导致了过程抽象不得不和大量局部状态打交道,虽然方便,但是也降低了可抽象和复用能力,而这本应该是过程抽象的目的。②存在大量的对类实例方法的级联调用(点号级联调用多简单呀) —— 这导致了数据抽象难以封闭,不能打造数据抽象屏障,无法解放心智。这两点即阻碍了数据抽象,也影响了过程抽象,简而言之,捆绑了开发者的手脚,降低了代码的表现能力。传统面向对象的一个典型的问题在于 null,有无数种策略被发明出来试图解决 NullPointerException 的问题,但却没一种好用 —— 造成空指针的最大问题在于级联调用,而级联调用不论是从设计模式还是从抽象的角度看,都是在贪婪的使用选择过程(类实例方法),因此除非开发者意识到过程更多指的是静态方法而非类实例方法(类实例方法应该仅用作操纵数据抽象的底层实现,用于静态方法或上下层数据抽象类使用以实现功能),空指针的问题才可能解决:只用简单的在静态类方法中实现过程抽象,为返回值使用 Optional、Either、Tuple 等函数式类型,简单的搭配 @NotNull 的入参和返回值即可解决这个问题。
最后,这里提到的消息传递风格仅仅是面向对象软件开发模式的静态结构部分,面向对象思想的模块化更多体现在对于状态的分割和隔离,使用计算机的时间来模拟物理世界的时间,更加贴合我们的思维。关于这部分内容也是优点缺点非常鲜明,在下一章主要介绍。
Ps. 在面向对象和设计模式中被广泛提到的“面向接口编程”其实本意应该是“不要打破数据抽象的封装”,后者并不是前者反向的论述,其包含范围更广,这里数据抽象的封装包括(a)数据不同表现形式的封装以及(b)数据抽象底层实现的封装。大部分设计模式教材中提到的“面向接口”更偏向前者 —— 接口和实现类的解耦,但实际上经典的设计模式在生产中比较少见,数据的多种表现形式并不总会有,但相反,数据的基础封装却很多,而往往被忽视的则总是不要破坏数据抽象这一部分 —— 在面向对象语言中,破坏数据抽象的典型表现就是级联调用方法,造成的恶果就是空指针异常。要立竿见影的解决这个问题,首先认识到类实例方法不是正常的过程,而是上下抽象层次沟通的通道,真正的过程应该定义在静态方法(伴生类)中,然后在需要级联调用的对象的静态方法中使用 Optional, Either 等函数式接口类型 + @Notnull 等注释包装,这样就完全不需要级联调用了。
LastUpdate:
- 2021-11-14 更新关于无状态面向对象的描述和 FP-OOP 糅合的建议。
- 2021-11-27 更新了关于无状态面向对象中高阶函数和返回对象的普通方法的论述。