Python数据处理学习笔记 - ndarray篇
这是我阅读《用Python进行数据分析》一书的笔记、实验和总结。总的来说,这本书主要介绍了Python的ndarray这一矢量化数据结构,基于numpy的pandas这一自动化表格处理(数据聚合、过滤、分析)工具,高质量2D出版物matplotlab这一图像生成工具。
这三大工具适合于对网络爬虫、网站监测等获取并保存在SQL、NoSQL甚至SQLite的数据进行处理。通俗来讲,它类似于表格处理工具Excel,可以进行数据过滤、分析和处理,也可以进行图像绘制和结果生成。不过显然,这三大工具不论是从操作方便性、简洁性、自动化还是图像质量、语言一致性上都远远超过VBA、宏和Excel。
第一篇文章主要介绍numpy的ndarray这一多维数组对象,这是Python进行数据分析的基石,也是保证大量数据处理速度的必要条件。这是第一篇文章。
1.一个简单的例子
如下所示,使用numpy创建随机数,可以看到,其区别于Python的random.random在于其多维属性。
import numpy as np
data1 = np.random.randn(2) # 0维数组就是一个随机数,1维为一个列表...
print(data1)
data = np.random.randn(2,3,4)
# randn返回一个正态分布数组,2-3-4 shaped,3维数组,
# 第一个维度为2个,第二个维度为3个,第三个维度为4个
# 最后一个维度表现为数字,其前面有三个括号
data
[-0.61465898 0.24995068]
array([[[-2.68468581, -1.79182648, 1.74420883, 0.03535622],
[-1.47181406, -1.37387988, -1.58428428, 1.04392948],
[ 0.22234194, 0.27470697, 1.04808109, 0.85817855]],
[[-0.47442726, 1.58605052, -1.66793281, -1.02318851],
[ 0.35110236, -1.10114907, 0.09977712, 0.08188061],
[ 1.13610052, -1.10023828, -0.44927535, 0.96697125]]])数据可以进行元素级别的加减乘除等运算,区别于Matlab,其所有算术运算都会广播道元素执行。
data * 10
data + data # 维度不变,算术运算对于各个维度子项目单独进行
array([[[-0.62805328, 0.13746167, -0.56001024, -4.62583189],
[-1.4894299 , -0.62518287, 2.44624749, -3.24258603],
[ 0.17639528, 1.11677586, 1.23353211, -2.11002009]],
[[-3.8480865 , 1.52970949, -0.69938998, -1.6610395 ],
[-1.33075899, -0.69120282, 2.99064208, -1.11083815],
[ 1.42852814, -0.7106241 , 1.15223994, 2.69708766]]])ndarray有三个重要的方法,shape方法返回结构信息,dtype方法返回元素类型,ndim返回维度信息。
print(data.shape) #(2, 3, 4) # 表示三个维度,每个维度有元素2,3,4
print(data.dtype) #float64
# 两个常用方法是模型和类型 dtype常见的还有int64和float64 除此之外还有Object和字符串
print(data.ndim) # ndim返回维度 3
2.ndarray对象概要
创建ndarray时可以声明其类型,使用dtype参数即可,但numpy会自动根据数据生成一个合适的类型,你也可以使用astype进行数据的转换。同样的,维度一般也会在声明时就确定,但是你亦然可以在创建后进行调整。
你可以使用list或者random、range、zeros等方法或者函数创建ndarray对象。
对于创建的对象可以使用ndarray.shape进行维度查看,使用reshape进行维度变换,比如ndarray.reshape((3,3))。使用ndarray.transpose()进行转置。
2.1 通过list创建ndarray
mydata = [1,2,3,3.5,5]
print(mydata,type(mydata))
data_new = np.array(mydata) # 可以使用np.array来将list转换成为ndarray对象
print(data_new,type(data_new))
mydata = [1,2,3,3.5,5,[3,1]]# 但是不规则数组难以转换
print(mydata,type(mydata))
try:
np.array(mydata)
except Exception as e:
print("不能转换=> ",e)
[1, 2, 3, 3.5, 5] <class 'list'>
[1. 2. 3. 3.5 5. ] <class 'numpy.ndarray'>
[1, 2, 3, 3.5, 5, [3, 1]] <class 'list'>
不能转换=> setting an array element with a sequence.2.2 特殊方法创建ndarray
常用的有zeros、empty、ones、arange、random.randn。
print(np.zeros(10)) # zeros可以创建全为0的ndarray,可以定义其维度,10为一维10个,3,6为2维
print(np.zeros((3, 6),dtype=int))
# 多维数组的创建需要放在一个元组中,注意不能写错,比如 np.zeros(3,6) 错误 应该为 np.zeros((3,6))
print(np.empty((2, 3, 2)))# empty创建一个填充垃圾数据的数组
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[[0 0 0 0 0 0]
[0 0 0 0 0 0]
[0 0 0 0 0 0]]
[[[0. 0.]
[0. 0.]
[0. 0.]]
[[0. 0.]
[0. 0.]
[0. 0.]]]np.arange(3,18,2,dtype=int) # numpy.arange([start, ]stop, [step, ]dtype=None)
array([ 3, 5, 7, 9, 11, 13, 15, 17])2.3 ndarray数据类型及转换
ndarray甚至和Python内置的列表都很不相同,因为ndarray需要保证所有的元素类型相同,而Python list则无此限制。ndarray需要保证每个元素长度相等,而Python list则可以不等长,支持任意嵌套。
ndarray常见的数据类型有np.int_(等同于C中long) float_(float64简写) string_ bool_ unicode(固定长度的unicode类型) etc. numpy的一大特点就是兼容C系的语言,因此有很多其他的类型以方便跨语言调用,比如float有float32,float64、int有int32,int64等,其中intc等同于C的int。
一般使用ndarray.dtype()进行数据类型的查看,使用ndarray.astype(type)进行类型转化。
arr1 = np.array([1, 2, 3], dtype=np.float64);arr2 = np.array([1, 2, 3], dtype=np.int32)
print(arr1.dtype);print(arr2.dtype) # float64 、int32
arr = np.array([1, 2, 3, 4, 5])
print(arr.dtype)
float_arr = arr.astype(np.float64)
# ndarray.astype(dtype, order='K', casting='unsafe', subok=True, copy=True)
print(float_arr.dtype) # int32 、float64
# ndarray.astype 可以拷贝一份新的格式转换的ndarray
arr = np.ones((2,3),dtype=np.int);print(arr)
arr2 = arr.astype(np.float);print(arr2)
[[1 1 1]
[1 1 1]]
[[1. 1. 1.]
[1. 1. 1.]]numeric_strings = np.array(['1.25', '-9.6', '42'], dtype=np.string_)
print(numeric_strings)
numeric_strings.astype(float)
[b'1.25' b'-9.6' b'42']
array([ 1.25, -9.6 , 42. ])int_array = np.arange(10)
calibers = np.array([.22, .270, .357, .380, .44, .50], dtype=np.float64)
int_array.astype(calibers.dtype)
# Returns array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])
3.索引和切片
对于一个数据结构,在内存中其占有一片空间区域。一般来说,我们能够对其进行的,就是使用FOR进行遍历。切片和索引是一种简化版的遍历方式,这提高了我们调用数据结构中某个元素的速度和方便程度。对于ndarray而言,索引和切片是处理其内部元素的一个重要构成部分。简要来说:
- 如果我们需要选取某一行列的内容,使用索引[n]。
- 如果要选取某几行列,并且这些行列连续,则使用切片[:]。
- 如果要选取某几行列,并且这些行列不连续,则使用花式索引[[m,n],[m,n]]。
- 如果需要按照某种条件进行索引,如果精确判断到元素级别,则使用bool型索引ndarray[bool判断表达式]。
- 如果需要按照某种条件进行索引,但是精确到行或者列或者需要对全或无进行判断,使用bool型索引后,使用any()和all()进行进一步判断。
3.1 基础用法
对于一维数组而言,其和list类型一样,[m:n]表示从m取到n,前包后不包,切片也是如此。所有的操作均是对原始array进行的。
对于多维数组而言,可以将多维数组看作是内嵌的列表,其操作基本相同,但有一点不同的地方是,不同维度的选取可以使用 [维度1] [维度2],还可以使用 [维度1,维度2]。冒号的作用和Python原生切片一样,也就是说,可以在各维度再进行冒号的元素级别选取。
对于元素级别的选取,其支持[a:b:c],其中a为起始元素位置,b为结束元素位置,包含a而不包含b,c为间隔选取距离。如果选取的元素位置不连续,那么使用[[0,2]]这样进行index为0和2的选取。比如第一个维度间隔2选取选取,而只选取第二个维度的0,2位置元素:[::2,[0,2]]
arr = np.array([[1,3,23],[23,33,211]]);print(arr)
print("\n")
print(arr[0,1])
# 切片可以使用逗号,表示从不同维度取值,对于一个二维数组,
# 只有一个切片,则返回此维度的内嵌维度所有元素。
print("\n",arr[0])
[[ 1 3 23]
[ 23 33 211]]
3
[ 1 3 23]arr[0] = 233
# 可以就地修改索引处的值,如果替代的是一个数组,但是只有一个字符串,则默认全部复制,
# 如果..arr[0] = [1,2,3,4] # 这个就会出错
print(arr)
[[233 233 233]
[ 23 33 211]]arr2d = np.array([[1,2,23],[3,34,111]])
print(arr2d[0][2]) # 23
print(arr2d[0, 2]) # 23 分号切片和list的嵌套列表切片本质上是一样的
Python默认索引有些简略的写法,比如冒号不写前面的则表示从头开始,不写后面的表示直到最后一个。
arr
arr[1:6]
arr2d
arr2d[:2]
arr2d[:2, 1:]
arr2d[1, :2]
arr2d[:2, 2]
arr2d[:, :1]
array([[1],
[3]])3.2 布尔型索引
Bool型索引就是纯Bool类型的一个ndarray,其一个好玩之处在于单个元素可以和整个数组进行==比较判断,而Python会自动判断每个元素和其是否相等并返回一个bool型的索引数组。也就是说,运算符可以生成bool型索引,而是用此索引可以从多维数组中获得元素。
本质上来说,numpy在进行ndarray和标量之间的算术运算时,重载了其魔术方法,如果你试图比较ndarray > 4,那么会自动广播到ndarray每一个元素进行比较,之后返回bool型数组。对于 == 也是这样。
bool型索引本质上是一个和ndarray等维的ndarray,其提供了很方便的根据条件对元素进行调整的办法。
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
data = ((np.random.randn(7, 4)+3)*10).astype(int)
print(names)
print(data)
['Bob' 'Joe' 'Will' 'Bob' 'Will' 'Joe' 'Joe']
[[13 31 43 47]
[27 17 30 41]
[58 18 31 43]
[40 12 21 26]
[ 4 28 24 33]
[41 32 52 19]
[45 26 17 30]]names == 'Bob' # 这个很好玩,因为对于Python标准数组来说,只能用 'Bob' in names
n_list = ['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'];
print("Bob in names?",'Bob' in n_list,'\n','Bob == list?','Bob' == n_list)
print(names == 'Bob') # 但是问题是,这是个表达式,谁生成了一个新数组?
Bob in names? True
Bob == list? False
[ True False False True False False False]一个bool列表可以对数组进行更为精细的操作,还可以叠加别的维度的操作
data[names == 'Bob'] # 相当于 data[0]和data[3]的合体,
# bool索引对于多维数组的可操作性更高,因为取出后必然要降维,
# 而是用一般的Python分片索引,取出后则很难继续将不同维度的数据合并。其类似于:
data[[True,False,False,False,False,False,True]] # 这是个诡异的写法,索引中嵌套了一个列表
array([[13, 31, 43, 47],
[45, 26, 17, 30]])print(data[names == 'Bob', 2:]) # 同样的,bool型数组可以作为第一维,可以继续对其他维度进行操作
print(data[names == 'Bob', 3])
[[43 47]
[21 26]]
[47 26]bool型列表可以保存,可以取反,甚至可以与逻辑操作符合起来使用
print(names != 'Bob')
print(data[~(names == 'Bob')]) # 取反只需要类似于RE中的波浪线标志即可
cond = names == 'Bob' # 这个bool列表可以保存起来下次继续用
print(data[~cond])
[False True True False True True True]
[[27 17 30 41]
[58 18 31 43]
[ 4 28 24 33]
[41 32 52 19]
[45 26 17 30]]
[[27 17 30 41]
[58 18 31 43]
[ 4 28 24 33]
[41 32 52 19]
[45 26 17 30]]print(names == 'Bob')
print(names == 'Will')
mask = (names == 'Bob') | (names == 'Will') # 逻辑或操作也可以
#mask = (names == 'Bob') & (names == 'Will') # 逻辑和操作也可以
print(mask)
data[mask]
[ True False False True False False False]
[False False True False True False False]
[ True False True True True False False]
array([[13, 31, 43, 47],
[58, 18, 31, 43],
[40, 12, 21, 26],
[ 4, 28, 24, 33]])bool型索引不仅仅可以由==,!=运算符生成,还可以由< > 等比较运算符生成
配合索引赋值,可以有效的操作数组的数据
data[data < 30] = 0 # 可以将data < 30 也看做一个bool型索引,比如:
res = (data < 30);print(res,res.dtype,res.shape)
data[res] = 0;print("\n",data)
[[False False False False]
[False False False False]
[False False False False]
[False False False False]
[False False False False]
[False False False False]
[False False False False]] bool (7, 4)
[[23333 31 43 47]
[23333 23333 30 41]
[ 58 23333 31 43]
[ 40 23333 23333 23333]
[23333 23333 23333 33]
[ 41 32 52 23333]
[ 45 23333 23333 30]]data[names != 'Joe'] = 7
data
array([[ 7, 7, 7, 7],
[23333, 23333, 30, 41],
[ 7, 7, 7, 7],
[ 7, 7, 7, 7],
[ 7, 7, 7, 7],
[ 41, 32, 52, 23333],
[ 45, 23333, 23333, 30]])3.3 布尔型索引的全部/存在判断
arr = np.random.randn(100);
print((arr > 0).sum()) # Returns 51
arr2 = np.array([True,False,False])
print(arr2.all()) # all为所有都是True吗? Returns False
print(arr2.any()) # any为存在为True的数吗? Returns True
all()可以指定axis轴以进行更为精确地判断
3.4 花式索引
区别于普通切片只是数组的引用,花式索引会返回一个新数组
如果说bool型索引是ndarray的亮点之一的话,那么花式索引则是ndarray的重中之重,因为传统的Python列表无法使用切片取出多维数据,而花式索引则解决了矩阵结构的不同维度数据存取问题。
arr = np.empty((8, 4))
for i in range(8):
arr[i] = i
arr
array([[0., 0., 0., 0.],
[1., 1., 1., 1.],
[2., 2., 2., 2.],
[3., 3., 3., 3.],
[4., 4., 4., 4.],
[5., 5., 5., 5.],
[6., 6., 6., 6.],
[7., 7., 7., 7.]])arr[[4, 3, 0, 6]]
array([[4., 4., 4., 4.],
[3., 3., 3., 3.],
[0., 0., 0., 0.],
[6., 6., 6., 6.]])arr[[-3, -5, -7]] #反向取值可以从尾部开始取,和python原生的[-1:]是取倒数第一行类似
array([[5., 5., 5., 5.],
[3., 3., 3., 3.],
[1., 1., 1., 1.]])print(np.arange(32))
arr = np.arange(32).reshape((8, 4)) # 等同于numpy.reshape(a, newshape, order='C')
# a = np.arange(6).reshape((3, 2));
# np.reshape(a, (2, 3)) 分别返回 array([[0, 1],[2, 3],[4, 5]])和array([[0, 1, 2],[3, 4, 5]])
print(arr)
arr[[1, 5, 7, 2], [0, 3, 1, 2]] # 叠加的花式索引
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31]
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]
[16 17 18 19]
[20 21 22 23]
[24 25 26 27]
[28 29 30 31]]
array([ 4, 23, 29, 10])3.5 花式索引的叠加和变维
花式索引不仅能够处理第一个维度的数据,还能够处理其余维度的数据,比如[:,[1,2,3]]这种写法
print(arr[[1,5,7,2]])
print(arr[[1, 5, 7, 2]][:, [0, 3, 1, 2]]) #类似于:
print(arr[[1,5,7,2]][[0,3,1,2]])
# 其实不是,这个写法只是两次花式索引,也就是调了两次位置,维度没有变化
# 要想维度变化的索引,可以使用: [;,[0,3,1,2]] 这种深入维度的索引,
# 其直接到了第三个维度,也就是元素维度进行操作
[[ 4 5 6 7]
[20 21 22 23]
[28 29 30 31]
[ 8 9 10 11]]
[[ 4 7 5 6]
[20 23 21 22]
[28 31 29 30]
[ 8 11 9 10]]
[[ 4 5 6 7]
[ 8 9 10 11]
[20 21 22 23]
[28 29 30 31]]
[[ 0 3 1 2]
[ 4 7 5 6]
[ 8 11 9 10]
[12 15 13 14]
[16 19 17 18]
[20 23 21 22]
[24 27 25 26]
[28 31 29 30]]arr = np.arange(24).reshape((2,3,4));print(arr)
arr[:,:,[0,2,1,3]]
# 可以直接调整第三个维度,前两个保持复制,但是 arr[[1,0],:,[0,2,13]]就不可以,
# 相反,使用此替代:
arr2 = arr[[1,0]][:,:,[0,2,1,3]];print(arr2)
[[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[[12 13 14 15]
[16 17 18 19]
[20 21 22 23]]]
[[[12 14 13 15]
[16 18 17 19]
[20 22 21 23]]
[[ 0 2 1 3]
[ 4 6 5 7]
[ 8 10 9 11]]]注意上面的写法,我们首先进行了一个花式索引,之后又对全新的数组进行了一个花式索引,直接调整第三个维度的数组,这里虽然可以直接调整第三个维度,但是不能直接在一个花式索引中完成所有步骤,因此分开做。
4.多维数组的排序
注意:ndarray.sort()是就地排序,而np.sort()则是复制一份新数据
arr = np.random.randn(6);print(arr)
arr.sort();print(arr)
[ 0.35565611 1.16969213 -1.32968207 0.69269737 -0.81785189 0.20410329]
[-1.32968207 -0.81785189 0.20410329 0.35565611 0.69269737 1.16969213]arr = np.random.randn(5, 3);print(arr)
arr.sort(1);print(arr)
[[-0.61301185 -0.59273517 0.8498737 ]
[ 0.7429723 -1.61620148 2.43280083]
[ 1.12530568 0.05152429 -0.0077932 ]
[ 0.1519599 0.37766685 -0.38625678]
[-0.11491053 -0.39637008 0.51807785]]
[[-0.61301185 -0.59273517 0.8498737 ]
[-1.61620148 0.7429723 2.43280083]
[-0.0077932 0.05152429 1.12530568]
[-0.38625678 0.1519599 0.37766685]
[-0.39637008 -0.11491053 0.51807785]]arr = np.array([[1,4],[3,1]]);print(arr);arr2 = arr.copy()
# 须知:使用copy才能复制一个数组,而使用[:]切片则不会
arr2.sort(axis=0);print(arr2);
arr.sort(axis=1);print(arr);
[[1 4]
[3 1]]
[[1 1]
[3 4]]
[[1 4]
[1 3]]复制一个数组,sort的numpy方法可以生成新的。使用copy也可以,使用花式索引也行,但是使用Python的[:]则不行——起码对于多维数组无效
arr = np.array([[1,4],[3,1]]);print("原始的arr值为\n",arr)
arr2 = arr[:];arr.sort();
print("对arr进行sort后,切片复制的arr2因为arr的改变而改变了\n",arr2);
print("现在的arr为:\n",arr)
arr3 = arr.copy(); print("但是使用copy命令的arr3则不变\n",arr3)
原始的arr值为
[[1 4]
[3 1]]
对arr进行sort后,切片复制的arr2因为arr的改变而改变了
[[1 4]
[1 3]]
现在的arr为:
[[1 4]
[1 3]]
但是使用copy命令的arr3则不变
[[1 4]
[1 3]]5.多维数组计算和统计基础
5.1 数组和数组、标量间的运算
数组和数组间的运算,如果维度相同则应用到元素级别;数组和标量之间的运算,则自动扩大到元素级别
arr = np.array([[1,2,3],[9,8,7]]);print(arr)
print(arr*arr,arr-0.5*arr,arr*0,sep="\n\n")
[[1 2 3]
[9 8 7]]
[[ 1 4 9]
[81 64 49]]
[[0.5 1. 1.5]
[4.5 4. 3.5]]
[[0 0 0]
[0 0 0]]和Matlab不同的是,numpy中使用np.dot(A,B)来计算A和B的乘积,而A*B则会对每个对应元素进行广播并求积。
5.2 通用函数:数学和统计方法
ndarray有很多通用函数,比如数学计算类,统计类和随机、步进生成类函数,这些函数使用很方便。
arr = np.arange(10)
arr
np.sqrt(arr)
np.exp(arr)
x = np.random.randn(8)
y = np.random.randn(8)
x
y
np.maximum(x, y)
arr = np.random.randn(7) * 5
arr
remainder, whole_part = np.modf(arr)
remainder
whole_part
arr
np.sqrt(arr)
np.sqrt(arr, arr)
arr
比如add()、sqrt()、sin()等数学方法,以及sun()、std()、mean()这种统计方法。所有的方法都可以直接对ndarray使用(面向对象),也可以调用np.method_name(ndarray)使用。
arr = np.random.randn(5, 4);print(arr)
print(arr.mean())
print(np.mean(arr))
print(arr.sum())
[[ 0.14869538 0.97301266 0.01436791 -0.35922877]
[-1.25616574 0.54107061 0.43904889 0.68787756]
[-1.45833961 0.50582051 -0.75305018 1.36064269]
[ 1.43912466 -1.2979654 -1.13902023 0.07277661]
[-2.19636042 1.14267716 -0.37483159 -0.71086429]]
-0.11103557942956728
-0.11103557942956728
-2.2207115885913455可以对轴进行单独的计算和统计,类似于Excel的表格计算统计数据
arr = np.array([[0,1,2],[1,2,3],[0,1,1]]);print(arr)
print("\n",arr.sum(axis=0))
print("\n",arr.sum(axis=1))
print("\n",arr.sum(axis=(0,1)))
# 0表示第一个轴,1表示第二个轴,传入一个tuple对象表示计算两轴总和
arr2 = np.array([[[0,1],[2,3]],[[4,5],[1,2]]]);
print(arr2,arr2.shape)
print("\n","第一个轴之和为\n",arr2.sum(axis=0))
# [0 1 2 3] + [4 5 1 2] 好玩的是其结果并非[4 6 3 5]而是[[4 6][3 5]],这点需要注意
print("\n","第二个轴之和为\n",arr2.sum(axis=1))
print("\n","第三个轴之和为\n",arr2.sum(axis=2))
[[0 1 2]
[1 2 3]
[0 1 1]]
[1 4 6]
[3 6 2]
11
[[[0 1]
[2 3]]
[[4 5]
[1 2]]] (2, 2, 2)
第一个轴之和为
[[4 6]
[3 5]]
第二个轴之和为
[[2 4]
[5 7]]
第三个轴之和为
[[1 5]
[9 3]]arr = np.array([0, 1, 2, 3, 4, 5, 6, 7])
arr.cumsum()
- cumsum / cumprod 返回累积和和累积乘积
- std / var 返回标准差和方差
- min / max 返回最大最小值
- mean 返回平均数
- sum 返回总和
- argmax / argmin 返回索引最大最小值
arr = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
arr
arr.cumsum(axis=0)
arr.cumprod(axis=1)
5.3 数组转置
使用ndarray的T方法,transpose方法或者swapaxes方法可以转置一个数据
所有的转置都是直接变换,不进行复制
arr = np.arange(15).reshape((3, 5));print(arr)
arr.T
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]]
array([[ 0, 5, 10],
[ 1, 6, 11],
[ 2, 7, 12],
[ 3, 8, 13],
[ 4, 9, 14]])arr = np.random.randn(6, 3);print(arr,arr.T,sep="\n\n")
np.dot(arr.T, arr) # 矩阵计算乘积
[[-0.84396988 0.20737763 0.45249126]
[-1.580369 1.93471643 0.77584114]
[-0.79764225 0.18855741 -0.8959513 ]
[ 0.32286382 0.07846277 -0.81797861]
[ 0.64822643 -0.6630227 -1.51781549]
[ 0.2819024 1.34665744 1.7859746 ]]
[[-0.84396988 -1.580369 -0.79764225 0.32286382 0.64822643 0.2819024 ]
[ 0.20737763 1.93471643 0.18855741 0.07846277 -0.6630227 1.34665744]
[ 0.45249126 0.77584114 -0.8959513 -0.81797861 -1.51781549 1.7859746 ]]
array([[ 4.44999201, -3.40781779, -1.63786897],
[-3.40781779, 6.08092881, 4.77319213],
[-1.63786897, 4.77319213, 7.77196467]])arr = np.arange(16).reshape((2, 2, 4));print(arr)
arr.transpose((1, 0, 2))
[[[ 0 1 2 3]
[ 4 5 6 7]]
[[ 8 9 10 11]
[12 13 14 15]]]
array([[[ 0, 1, 2, 3],
[ 8, 9, 10, 11]],
[[ 4, 5, 6, 7],
[12, 13, 14, 15]]])arr
arr.swapaxes(1, 2)
6.多元数组表达式基础
6.1 迭代,切分和合并
ndarray使用for循环迭代结果如下,可以看到,一次迭代返回行,二次迭代返回行元素。
a = array(
[[92, 94, 73, 65],
[94, 52, 97, 64],
[46, 88, 43, 14],
[51, 50, 69, 46]])
for x in a:
print(x) #x为[92 94 73 65]
for y in x:
print(y) #y为92
break
break
#使用ndarray.flat可以拍平数组为1维,然后变成一个列表,直接输出。
for x in a.flat:
print(x) #92 94 73 65 94 52 ...对于合并而言,使用全局函数np.v(h)stack进行栈在不同方向上的合并:
a = np.zeros((3,3))
b = np.ones((3,3))
c = np.random.randint(10,100,size=(3,4))
np.vstack((a,b)) #a,c不能垂直合并
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
np.hstack((a,c,b)) #注意stack接受的值要放在一个tuple中。
array([[ 0., 0., 0., 99., 77., 21., 15., 1., 1., 1.],
[ 0., 0., 0., 92., 74., 48., 31., 1., 1., 1.],
[ 0., 0., 0., 66., 16., 66., 70., 1., 1., 1.]])使用split进行切分:
numpy.split(ary, indices_or_sections, axis=0)
#其中ary为需要切分的原数组,
#第二个参数为切片,比如[2,4]是切三片,第二片为[2,4)
#第三个参数指定工作的轴。
#除了使用split,还可以使用hsplit、vsplit进行水平和垂直切分。
d=[[ 0. 0. 0. 99. 77. 21. 15. 1. 1. 1.]
[ 0. 0. 0. 92. 74. 48. 31. 1. 1. 1.]
[ 0. 0. 0. 66. 16. 66. 70. 1. 1. 1.]]
np.split(d,[3,6],axis=1)
[ array([
[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]),
array([
[99., 77., 21.],
[92., 74., 48.],
[66., 16., 66.]]),
array([
[15., 1., 1., 1.],
[31., 1., 1., 1.],
[70., 1., 1., 1.]])
] #切片结果为一个list。6.2 条件逻辑的矢量化运算:np.where
使用np.where可以将 x if cond else y 表示成 np.where(cond,x,y)
其中cond可以为bool型索引,也可以为表达式,比如 [T,F,F,T] or arr > 5.
另外,np.where可以嵌套,比如 arr=np.were(cond1,np.where(cond2,x,y),z)
xarr = np.array([1.1, 1.2, 1.3, 1.4, 1.5])
yarr = np.array([2.1, 2.2, 2.3, 2.4, 2.5])
cond = np.array([True, False, True, True, False])
result = np.where(cond, xarr, yarr)
result
array([1.1, 2.2, 1.3, 1.4, 2.5])arr = np.random.rand(4,4);print(arr)
arr2 = np.where(arr > 0.5,0,arr*10);print(arr2)
[[0.53360993 0.75904481 0.41544517 0.82982399]
[0.99958328 0.26709263 0.68368172 0.98439953]
[0.57353012 0.63552816 0.27177872 0.75717192]
[0.55308005 0.83160888 0.55769017 0.13227596]]
[[0. 0. 4.1544517 0. ]
[0. 2.67092631 0. 0. ]
[0. 0. 2.71778721 0. ]
[0. 0. 0. 1.32275961]]6.3 唯一、存在的判断:unique,is1d,isin
names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
print(np.unique(names),names) #unique仅复制而不改变原有数组
ints = np.array([3, 3, 3, 2, 2, 1, 1, 4, 4])
np.unique(ints)
['Bob' 'Joe' 'Will'] ['Bob' 'Joe' 'Will' 'Bob' 'Will' 'Joe' 'Joe']
array([1, 2, 3, 4])sorted(set(names)) => ['Bob', 'Joe', 'Will']
np.in1d() 测试一个list在另外一个list中是否存在,对被比较list的每个值进行比较,返回一个bool型数组
values = np.array([6, 0, 0, 3, 2, 5, 6])
np.in1d(values, [2, 3, 6])
array([ True, False, False, True, True, False, True])np.isin()可以判断一个元素是否在另一个元素内,返回一个bool型数组。
element = array([[0, 2],
[4, 6]])
test_elements = [1, 2, 4, 8]
mask = np.isin(element, test_elements)
#结果是;
array([[ False, True],
[ True, False]])7.矢量化运算基础
7.1 广播和矩阵
使用数组表达式代替循环的方法称之为矢量化,其速度更快。
meshgrid为广播,其接受两个一维数组并产生两个T变换的二维矩阵,这两个二维矩阵对应所有的(x,y)对。
points = np.arange(-5, 5, 0.01) # 1000 equally spaced points
print(points.shape)
xs, ys = np.meshgrid(points, points) # 将一维数组扩充为2维数组,在第二个维度单纯复制。
# xs为一维数组横向形式,纵向赋值,ys为纵向形式,横向复制
print(xs,ys,sep="\n\n\n");print(xs.dtype,xs.shape)
(1000,)
[[-5. -4.99 -4.98 ... 4.97 4.98 4.99]
[-5. -4.99 -4.98 ... 4.97 4.98 4.99]
[-5. -4.99 -4.98 ... 4.97 4.98 4.99]
...
[-5. -4.99 -4.98 ... 4.97 4.98 4.99]
[-5. -4.99 -4.98 ... 4.97 4.98 4.99]
[-5. -4.99 -4.98 ... 4.97 4.98 4.99]]
[[-5. -5. -5. ... -5. -5. -5. ]
[-4.99 -4.99 -4.99 ... -4.99 -4.99 -4.99]
[-4.98 -4.98 -4.98 ... -4.98 -4.98 -4.98]
...
[ 4.97 4.97 4.97 ... 4.97 4.97 4.97]
[ 4.98 4.98 4.98 ... 4.98 4.98 4.98]
[ 4.99 4.99 4.99 ... 4.99 4.99 4.99]]
float64 (1000, 1000)z = np.sqrt(xs ** 2 + ys ** 2)
z
array([[7.07106781, 7.06400028, 7.05693985, ..., 7.04988652, 7.05693985,
7.06400028],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
...,
[7.04988652, 7.04279774, 7.03571603, ..., 7.0286414 , 7.03571603,
7.04279774],
[7.05693985, 7.04985815, 7.04278354, ..., 7.03571603, 7.04278354,
7.04985815],
[7.06400028, 7.05692568, 7.04985815, ..., 7.04279774, 7.04985815,
7.05692568]])%matplotlib inline
import matplotlib.pyplot as plt
plt.imshow(z, cmap=plt.cm.gray); plt.colorbar()
plt.title("Image plot of $\sqrt{x^2 + y^2}$ for a grid of values")
Text(0.5,1,'Image plot of $\\sqrt{x^2 + y^2}$ for a grid of values')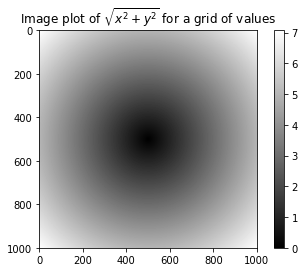
plt.draw()
plt.close('all')
7.2 线性代数相关
python numpy提供的线性代数包为numpy.linalg。和matlab有区别,numpy的*是元素级别的,而np.dot(x,y)或者x.dot(y)才是矩阵乘积
x = np.array([[1., 2., 3.], [4., 5., 6.]])
y = np.array([[6., 23.], [-1, 7], [8, 9]])
print(x)
print(y)
x.dot(y)
[[1. 2. 3.]
[4. 5. 6.]]
[[ 6. 23.]
[-1. 7.]
[ 8. 9.]]
array([[ 28., 64.],
[ 67., 181.]])np.dot(x, y)
np.dot(x, np.ones(3))
x @ np.ones(3)
from numpy.linalg import inv, qr
X = np.random.randn(5, 5)
mat = X.T.dot(X)
inv(mat)
mat.dot(inv(mat))
q, r = qr(mat)
r
7.3 随机数生成
可以使用numpy.random.normal(loc=0.0, scale=1.0, size=None)生成标准分布随机数,比如:
s = np.random.normal(0,0.1,(4,4)) # 平均数为0,标准差为0.1 4*4维数组
s
array([[-0.03907376, 0.12275294, 0.05882021, -0.01106293],
[-0.04382717, 0.03827646, 0.12300646, -0.07722948],
[ 0.00270246, 0.10688825, -0.04299091, -0.09184912],
[-0.01651154, 0.21520002, -0.01527374, -0.09653402]])mu = 0;sigma = 0.1
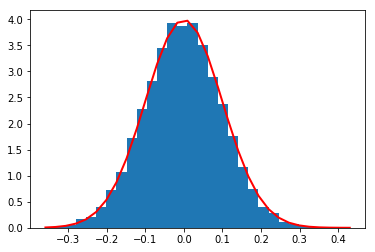
s = np.random.normal(mu,sigma,10000)
import matplotlib.pyplot as plt
count, bins, ignored = plt.hist(s, 30, normed=True)
plt.plot(bins, 1/(sigma * np.sqrt(2 * np.pi)) *
np.exp( - (bins - mu)**2 / (2 * sigma**2) ),
linewidth=2, color='r')
plt.show()
from random import normalvariate
N = 1000000
%timeit samples = [normalvariate(0, 1) for _ in range(N)]
%timeit np.random.normal(size=N)
1.06 s ± 36.5 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
45.7 ms ± 1.81 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)np.random.seed(1234)
np.random.rand()
0.1915194503788923rand()产生随机数,randn()产生标准正态分布,normal()产生高斯正态分布,binormal产生二项分布,randint()产生有边界的随机数
shuffle()对一个序列进行随机排列 chiquare产生卡方分布
np.random.uniform() # 产生[0,1)直接均匀的分布样本值
print(np.random.binomial(10,0.5,100)) # 产生二项分布随机值
arr = np.arange(10); np.random.shuffle(arr); print("\n",arr)
[3 5 6 6 3 5 6 6 3 4 2 6 3 3 2 5 6 6 5 7 7 7 4 7 6 6 3 6 5 7 3 7 8 5 5 4 4
8 6 5 6 5 6 5 2 5 4 6 6 6 6 7 6 7 1 5 7 5 6 4 2 4 5 5 4 6 7 6 7 7 4 6 4 6
7 5 4 3 6 2 5 7 6 8 2 6 6 4 3 5 4 3 5 2 4 4 8 5 4 2]
[3 8 5 0 6 9 4 7 1 2]8.多维数组文件读写
可以使用 np.load() 和 np.save() 来保存以及加载二进制文件,其格式为npy。使用 savez() 可以保存多个文件到一个压缩文件中,其格式为npz,数组作为参数传递。
arr = np.arange(10)
np.save('some_array', arr)
np.load('some_array.npy')
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])np.savez("lotofarray", a=arr, b=arr)
arch = np.load('array_archive.npz');print(arch,arch.files)
arch['b'] #类似于字典的方式取出相应参数,使用files查看所包含的参数
<numpy.lib.npyio.NpzFile object at 0x000000CD76D3A358> ['a', 'b']
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])np.savez_compressed('arrays_compressed.npz', a=arr, b=arr)
此外,numpy还给出了读取txt以及保存txt文件的方法,可以直接读取为array,比如 loadtxt 和 savetxt。
np.savetxt("savedtxt",arr,delimiter="::")
np.loadtxt("savedtxt",delimiter="::")
array([0., 1., 2., 3., 4., 5., 6., 7., 8., 9.])9.例子:随机漫步
1000次漫步
import random
position = 0
walk = [position]
steps = 1000
for i in range(steps):
step = 1 if random.randint(0, 1) else -1
position += step
walk.append(position)
%matplotlib inline
plt.figure()
<matplotlib.figure.Figure at 0xcd7f99cbe0>
<matplotlib.figure.Figure at 0xcd7f99cbe0>plt.plot(walk[:100])
[<matplotlib.lines.Line2D at 0xcd0368bd30>]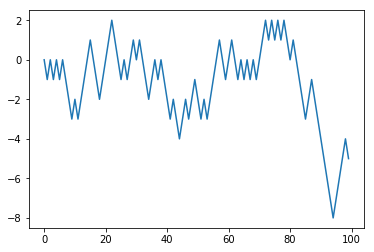
np.random.seed(12345)
nsteps = 1000
draws = np.random.randint(0, 2, size=nsteps);#print(draws)
steps = np.where(draws > 0, 1, -1);#print(steps)
walk = steps.cumsum();#print(walk) # numpy.cumsum(a, axis=None, dtype=None, out=None)[source]
# Return the cumulative sum of the elements along a given axis.
plt.plot(walk)
print(walk.min())
print(walk.max())
-21
15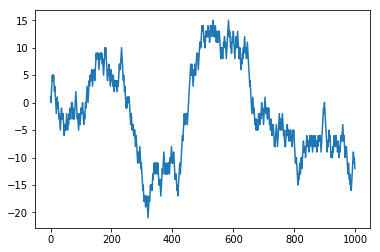
(np.abs(walk) >= 10).argmax() # numpy.argmax(a, axis=None, out=None)[source]
# Returns the indices of the maximum values along an axis.
1795000次模拟1000次漫步
nwalks = 5000
nsteps = 1000
draws = np.random.randint(0, 2, size=(nwalks, nsteps)) # 0 or 1
steps = np.where(draws > 0, 1, -1)
walks = steps.cumsum(1)
print(walks,walks.shape)
[[ -1 0 1 ... -18 -17 -18]
[ -1 -2 -1 ... 0 -1 0]
[ 1 0 1 ... 18 19 20]
...
[ 1 2 1 ... -2 -3 -2]
[ 1 2 3 ... 22 21 20]
[ -1 -2 -1 ... 26 25 26]] (5000, 1000)print(walks.max())
print(walks.min())
138
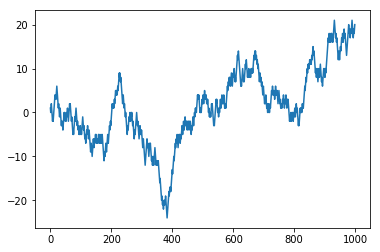
-133plt.draw()
plt.plot(walks[2][:1000])
plt.show()
hits30 = (np.abs(walks) >= 30).any(1) # 不是所有5000次都达到了30,any表示一次即可
hits30 # Test whether any array element along a given axis evaluates to True.
hits30.sum() # Number that hit 30 or -30
3412crossing_times = (np.abs(walks[hits30]) >= 30).argmax(1)
crossing_times.mean()
499.0468933177022steps = np.random.normal(loc=0, scale=0.25,
size=(nwalks, nsteps))
更新历史:
2018-02-23 阅读《利用Python进行数据分析》并撰写笔记
2018-03-22 阅读《Python数据分析实战》 并修改笔记,添加了numpy迭代、split和stack的介绍。整理了目录。
2018-03-27 细节调整。增加了argmax、argmin的介绍。
2018-04-25 细节调整。